Deck 7: Symmetric Matrices and Quadratic Forms
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/25
Play
Full screen (f)
Deck 7: Symmetric Matrices and Quadratic Forms
1
Orthogonally diagonalize the matrix, giving an orthogonal matrix P and a diagonal matrix D.


C
2
Find a singular value decomposition of the matrix A.


D
3
Make a change of variable, x = Py, that transforms the given quadratic form into a quadratic form with no cross-product
term. Give P and the new quadratic form.
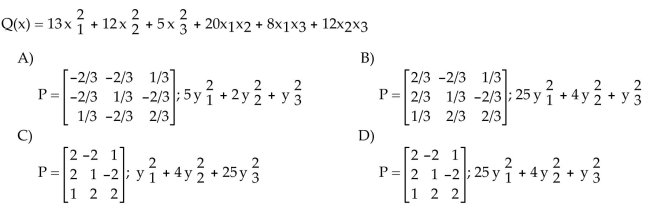
term. Give P and the new quadratic form.
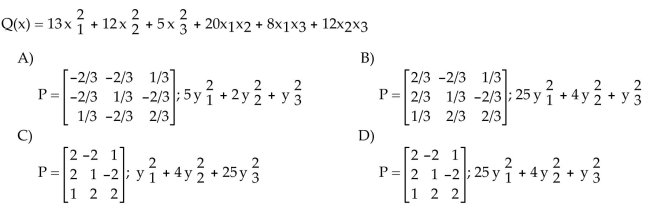
B
4
Find the singular values of the matrix.



Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
5
Find the matrix of the quadratic form.
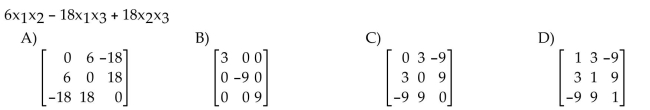
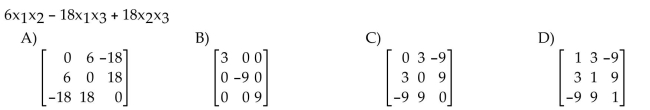

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
6
Find the singular values of the matrix.



Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
7
Orthogonally diagonalize the matrix, giving an orthogonal matrix P and a diagonal matrix D.
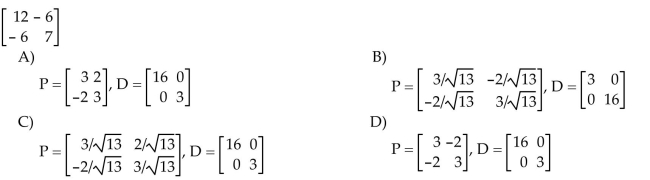
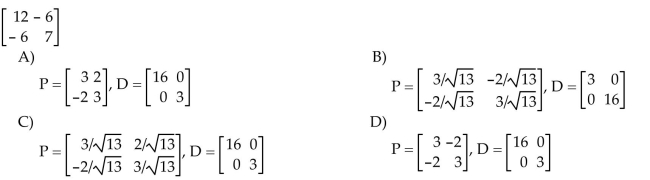

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
8
Find the matrix of the quadratic form.



Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
9
Orthogonally diagonalize the matrix, giving an orthogonal matrix P and a diagonal matrix D.
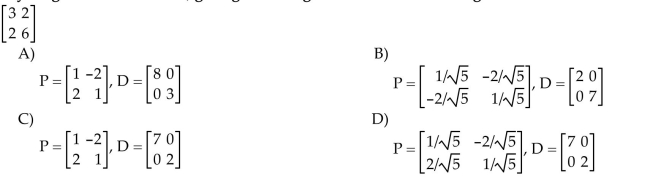
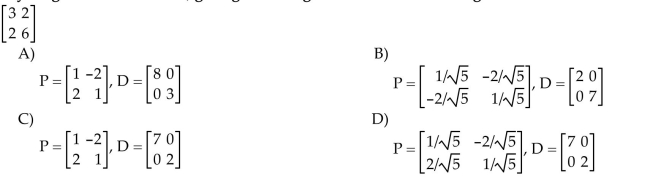

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
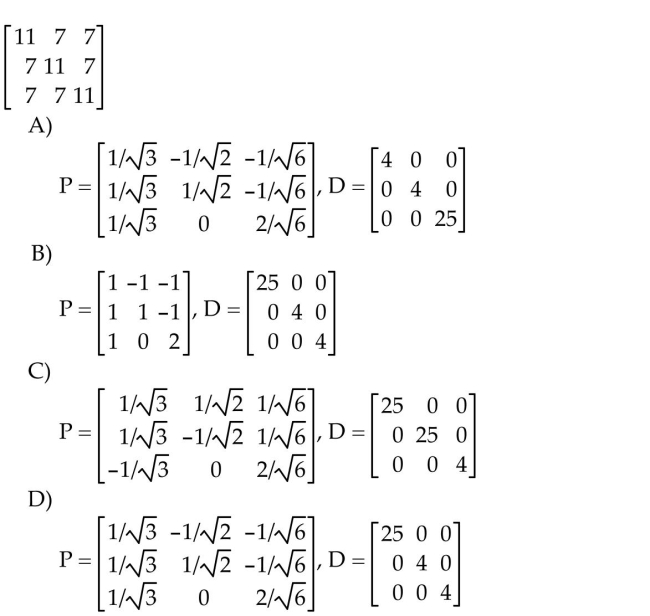
10
Orthogonally diagonalize the matrix, giving an orthogonal matrix P and a diagonal matrix D.


Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
11
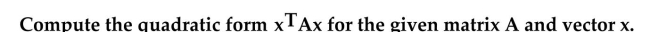
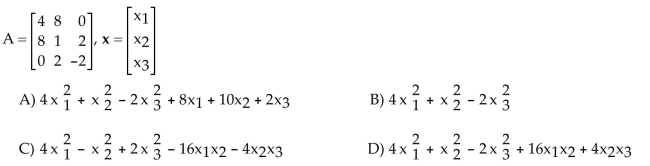

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
12
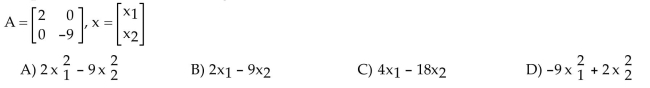

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
13

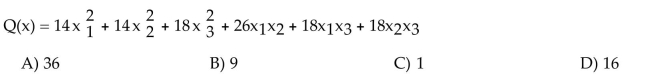

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
14
Make a change of variable, x = Py, that transforms the given quadratic form into a quadratic form with no cross-product
term. Give P and the new quadratic form.
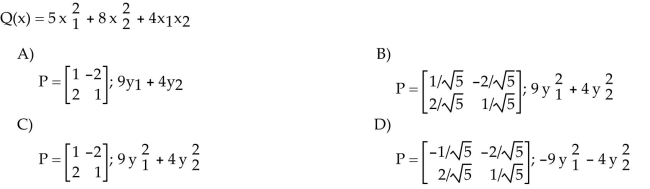
term. Give P and the new quadratic form.
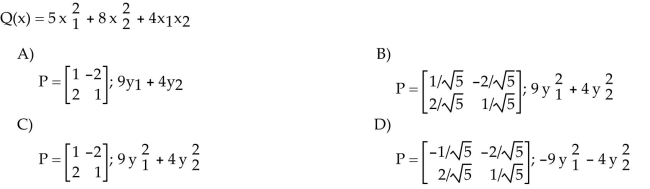

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
15
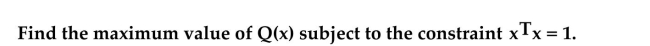


Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
16
Determine whether the matrix is symmetric.



Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
17
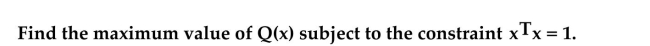
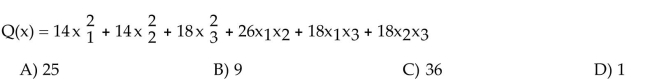

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
18
Find a singular value decomposition of the matrix A.
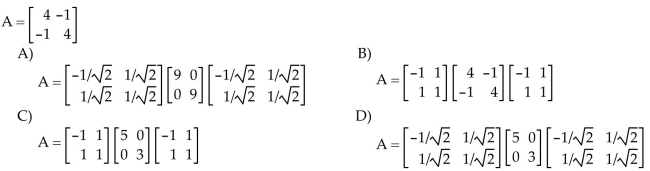
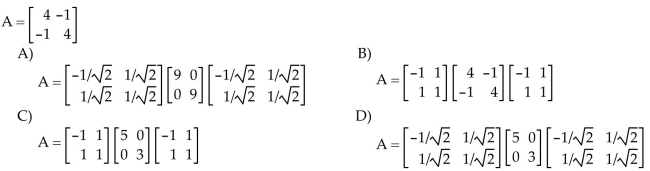

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
19



Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
20
Determine whether the matrix is symmetric.



Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
21
Use the given covariance matrix to compute the percentage of the total variance that is contained in the first principal
component. Round to one decimal place.
component. Round to one decimal place.


Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
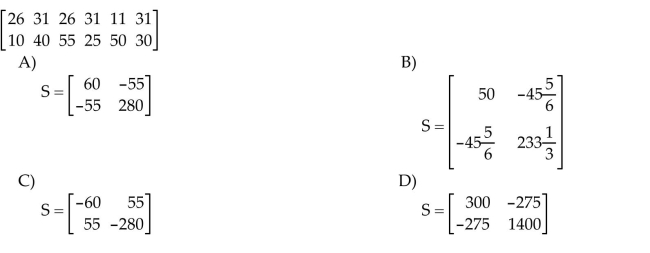
22
Use the given covariance matrix to compute the percentage of the total variance that is contained in the first principal
component. Round to one decimal place.
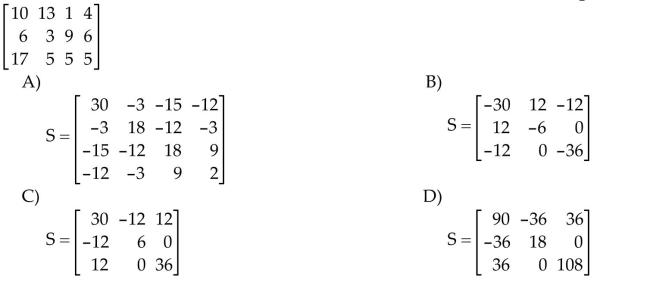
component. Round to one decimal place.
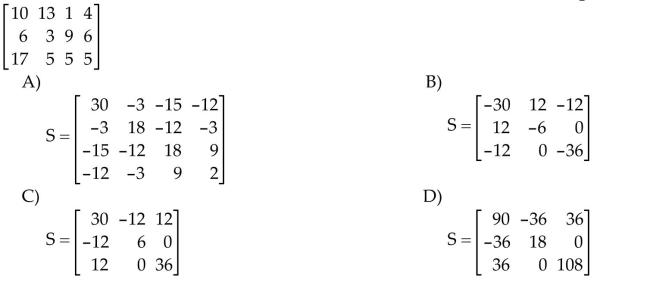

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
23
Find a singular value decomposition of the matrix A.



Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
24
Convert the matrix of observations to mean-deviation form, and construct the sample covariance matrix.



Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
25
Convert the matrix of observations to mean-deviation form, and construct the sample covariance matrix.



Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck


