Deck 4: Vector Spaces
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/47
Play
Full screen (f)
Deck 4: Vector Spaces
1
Find a matrix A such that W = Col A.
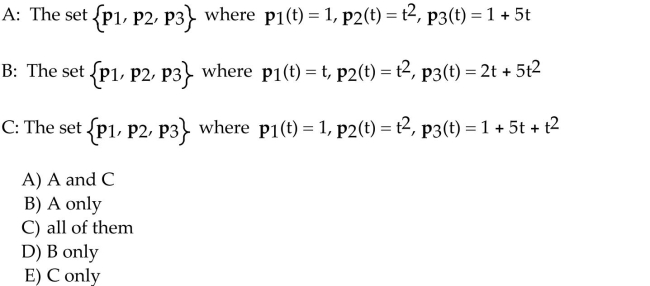
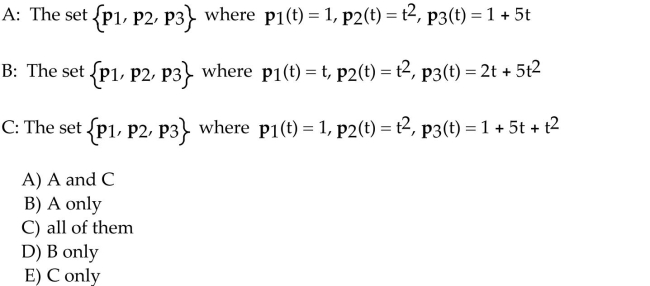
D
2
If the set W is a vector space, find a set S of vectors that spans it. Otherwise, state that W is not a vector space.
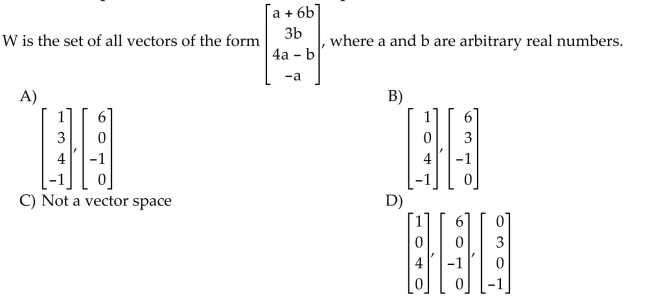

B
3
Solve the problem.


A
4
Find a matrix A such that W = Col A.
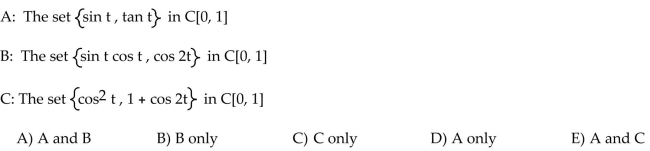
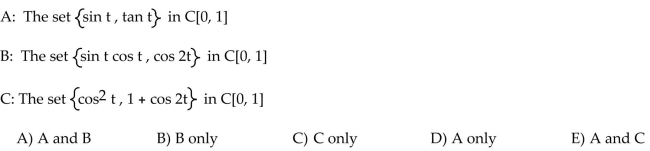

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
5
Find a matrix A such that W = Col A.
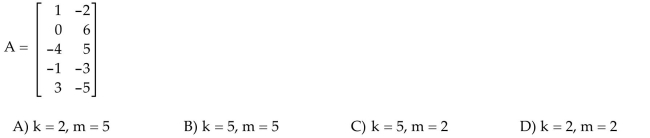
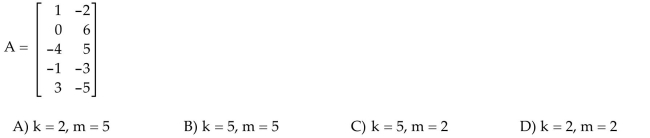

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
6
If the set W is a vector space, find a set S of vectors that spans it. Otherwise, state that W is not a vector space.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
7
Determine whether the vector u belongs to the null space of the matrix A.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the problem.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the problem.
Let H be the set of all polynomials having degree at most 4 and rational coefficients. Determine whether H is a vector space. If it is not a vector space, determine which of the following properties
It fails to satisfy.
A: Contains zero vector
B: Closed under vector addition
C: Closed under multiplication by scalars
A)H is not a vector space; not closed under multiplication by scalars
B)H is not a vector space; does not contain zero vector
C)H is a vector space.
D)H is not a vector space; not closed under vector addition
Let H be the set of all polynomials having degree at most 4 and rational coefficients. Determine whether H is a vector space. If it is not a vector space, determine which of the following properties
It fails to satisfy.
A: Contains zero vector
B: Closed under vector addition
C: Closed under multiplication by scalars
A)H is not a vector space; not closed under multiplication by scalars
B)H is not a vector space; does not contain zero vector
C)H is a vector space.
D)H is not a vector space; not closed under vector addition

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
10
Determine whether the vector u belongs to the null space of the matrix A.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the problem.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
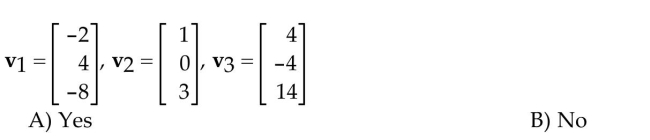
12
Determine which of the sets of vectors is linearly independent.


Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
13
Find an explicit description of the null space of matrix A by listing vectors that span the null space.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
14
Determine if the vector u is in the column space of matrix A and whether it is in the null space of A.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
15
Determine if the vector u is in the column space of matrix A and whether it is in the null space of A.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
16
Find an explicit description of the null space of matrix A by listing vectors that span the null space.
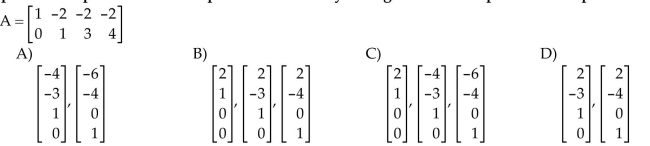
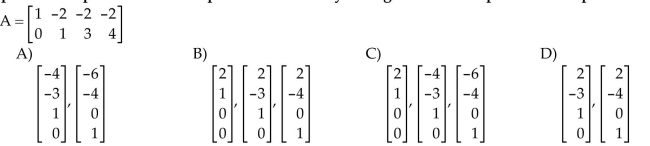

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
17
Determine which of the sets of vectors is linearly independent.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
18
Find a matrix A such that W = Col A.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the problem.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
20
Solve the problem.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
21
Find a basis for the column space of the matrix.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
22
Assume that the matrix A is row equivalent to B. Find a basis for the row space of the matrix A.
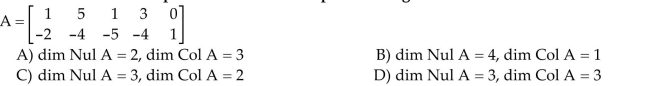
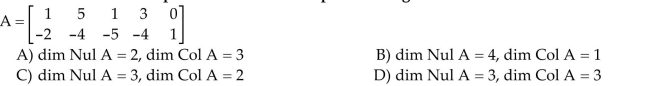

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
23
Find the specified change-of-coordinates matrix.
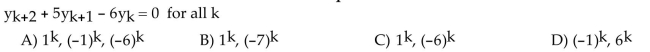
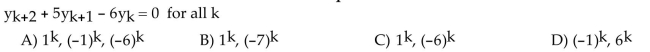

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
24
Determine whether the signals are linearly independent.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
25
Determine whether the signals are linearly independent.
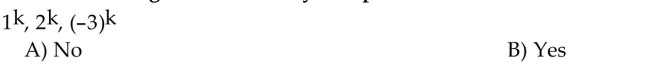
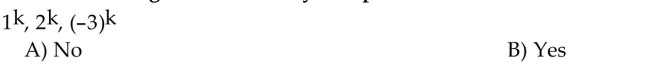

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
26
Solve the problem.
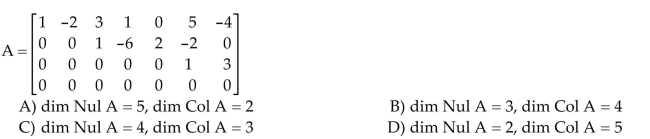
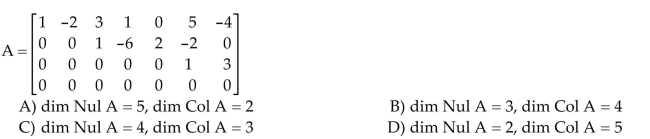

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
27
Determine which of the sets of vectors is linearly independent.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
28
Determine whether {v1, v2, v3} is a basis for
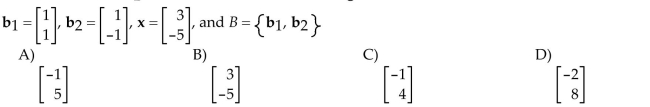
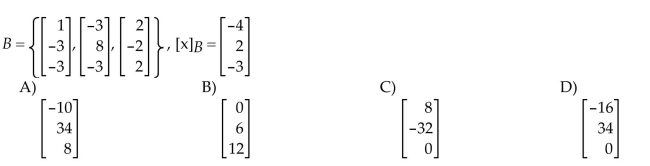
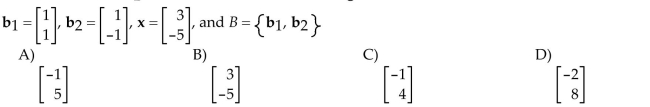


Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
29
Find a basis for the column space of the matrix.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
30
Find the new coordinate vector for the vector x after performing the specified change of basis.
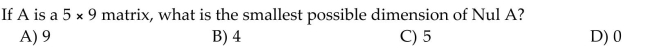

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
31
Determine whether {v1, v2, v3} is a basis for
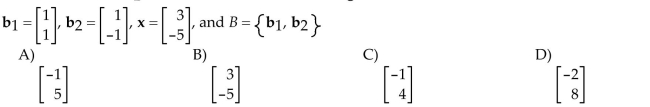
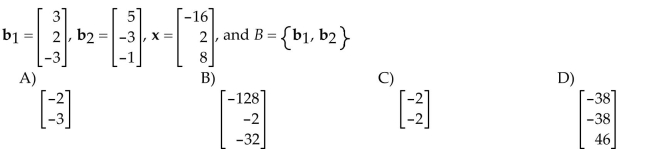
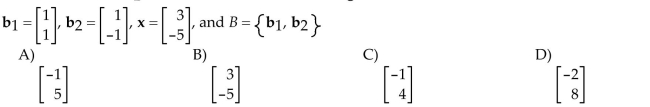
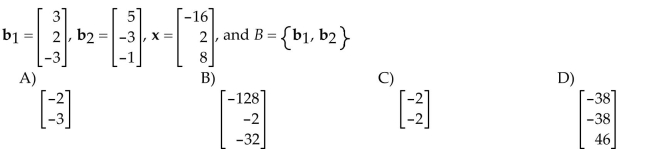

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
32
Find a basis for the set of all solutions to the difference equation.
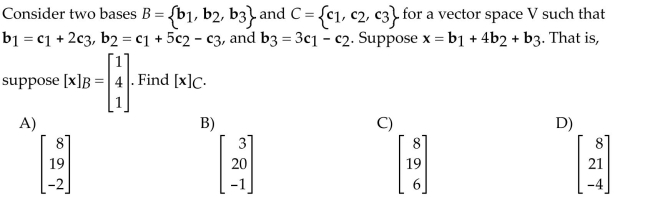
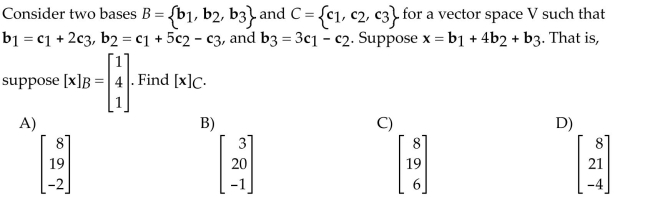

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
33
Determine which of the sets of vectors is linearly independent.
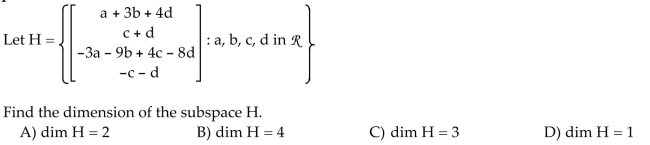
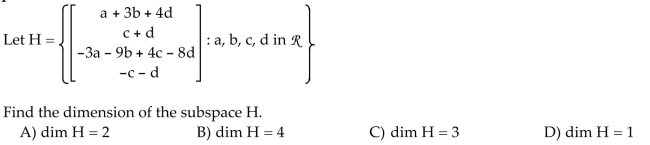

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the problem.
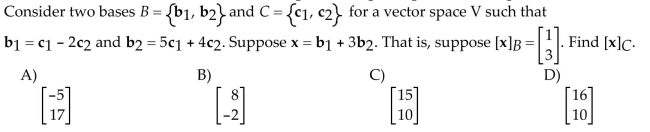
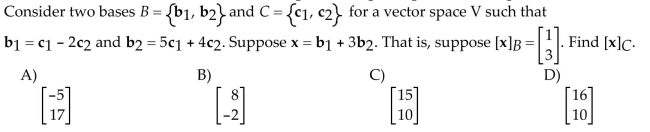

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
35
Determine which of the sets of vectors is linearly independent.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
36
Find the new coordinate vector for the vector x after performing the specified change of basis.
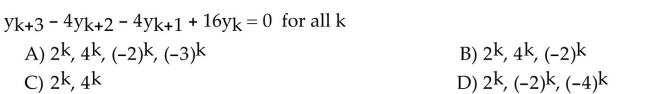
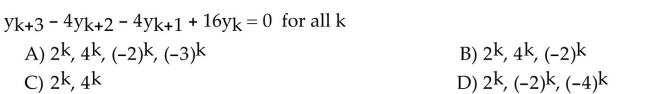

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
37
Solve the problem.
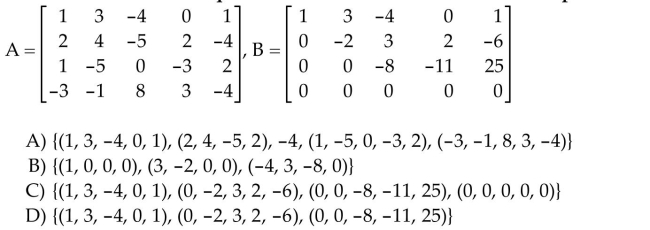
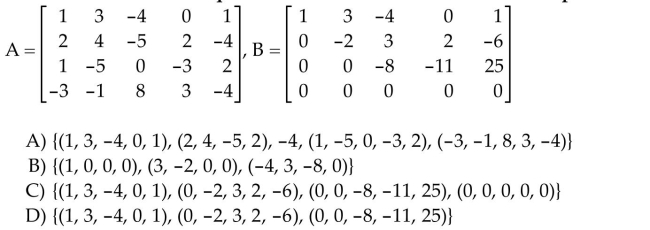

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
38
Solve the problem.
A mathematician has found 5 solutions to a homogeneous system of 40 equations in 42
variables. The 5 solutions are linearly independent and all other solutions can be
constructed by adding together appropriate multiples of these 5 solutions. Will the system
necessarily have a solution for every possible choice of constants on the right side of the
equation? Explain.
A mathematician has found 5 solutions to a homogeneous system of 40 equations in 42
variables. The 5 solutions are linearly independent and all other solutions can be
constructed by adding together appropriate multiples of these 5 solutions. Will the system
necessarily have a solution for every possible choice of constants on the right side of the
equation? Explain.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
39
Find the specified change-of-coordinates matrix.
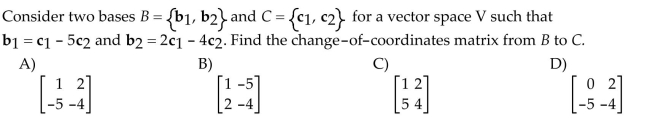
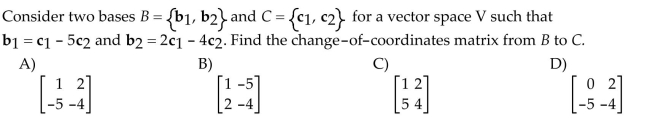

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the problem.
Suppose a nonhomogeneous system of 15 linear equations in 17 unknowns has a solution
for all possible constants on the right side of the equation. Is it possible to find 3 nonzero
solutions of the associated homogeneous system that are linearly independent? Explain.
Suppose a nonhomogeneous system of 15 linear equations in 17 unknowns has a solution
for all possible constants on the right side of the equation. Is it possible to find 3 nonzero
solutions of the associated homogeneous system that are linearly independent? Explain.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
41
Find the general solution of the difference equation.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
42
Find a basis for the set of all solutions to the difference equation.
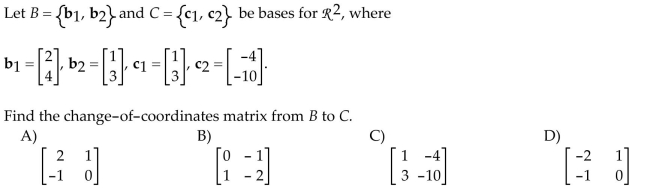
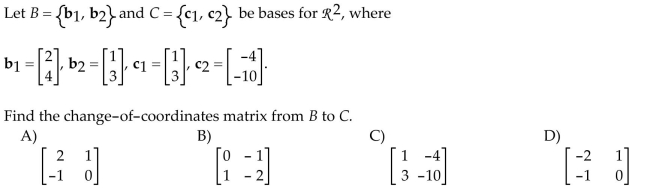

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
43
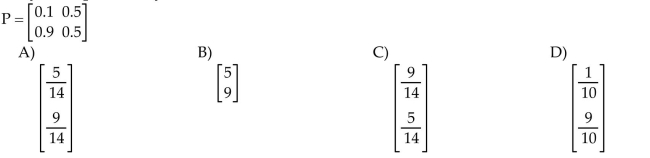
Find the steady-state probability vector for the stochastic matrix P.


Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
44
Find the steady-state probability vector for the stochastic matrix P.
Suppose that demographic studies show that each year about 8% of a cityʹs population moves to the suburbs (and 92% stays in the city), while 4% of the suburban population moves to the city
(and 96% remains in the suburbs). In the year 2000, 64.1% of the population of the region lived in
The city and 35.9% lived in the suburbs. What percentage of the population of the region would
Eventually live in the city if the migration probabilities were to remain constant over many years?
For simplicity, ignore other influences on the population such as births, deaths, and migration into
And out of the region.
A)66.7%
B)50%
C)41.7%
D)33.3%
Suppose that demographic studies show that each year about 8% of a cityʹs population moves to the suburbs (and 92% stays in the city), while 4% of the suburban population moves to the city
(and 96% remains in the suburbs). In the year 2000, 64.1% of the population of the region lived in
The city and 35.9% lived in the suburbs. What percentage of the population of the region would
Eventually live in the city if the migration probabilities were to remain constant over many years?
For simplicity, ignore other influences on the population such as births, deaths, and migration into
And out of the region.
A)66.7%
B)50%
C)41.7%
D)33.3%

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
45
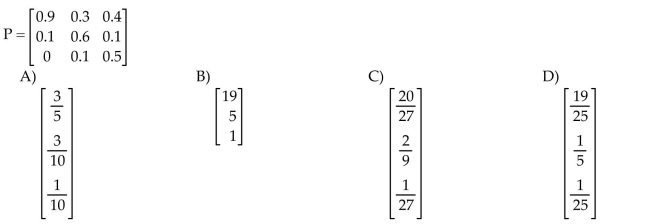
Find the steady-state probability vector for the stochastic matrix P.


Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
46
Find the general solution of the difference equation.



Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the problem.
Suppose that demographic studies show that each year about 6% of a cityʹs population moves to the suburbs (and 94% stays in the city), while 4% of the suburban population moves to the city
(and 96% remains in the suburbs). In the year 2000, 64% of the population of the region lived in the
City and 36% lived in the suburbs. What is the distribution of the population in 2002? For
Simplicity, ignore other influences on the population such as births, deaths, and migration into and
Out of the city/suburban region.
A)61.6% in the city and 38.4% in the suburbs
B)60.5% in the city and 39.5% in the suburbs
C)59.4% in the city and 40.6% in the suburbs
D)58.3% in the city and 41.7% in the suburbs
Suppose that demographic studies show that each year about 6% of a cityʹs population moves to the suburbs (and 94% stays in the city), while 4% of the suburban population moves to the city
(and 96% remains in the suburbs). In the year 2000, 64% of the population of the region lived in the
City and 36% lived in the suburbs. What is the distribution of the population in 2002? For
Simplicity, ignore other influences on the population such as births, deaths, and migration into and
Out of the city/suburban region.
A)61.6% in the city and 38.4% in the suburbs
B)60.5% in the city and 39.5% in the suburbs
C)59.4% in the city and 40.6% in the suburbs
D)58.3% in the city and 41.7% in the suburbs

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck


