Deck 4: Systems of Equations and Inequalities
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/131
Play
Full screen (f)
Deck 4: Systems of Equations and Inequalities
1
Determine whether the ordered pair is a solution of the system of linear equations
A) Yes
B) No
A) Yes
B) No
A
2
Solve the system of equations by the substitution method.
A)
B)
C)
D)
A)
B)
C)
D)
B
3
Solve the system of equations by the elimination method.
A)
B)
C)
D)
A)
B)
C)
D)
A
4
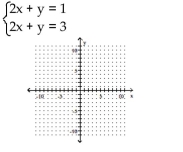 A)
A) В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
5
Solve the system of equations by the elimination method.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
6
Solve the system of equations by the elimination method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
7
Solve the system of equations by the substitution method.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
8
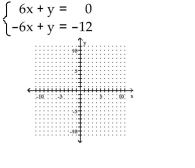 A)
A) B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
9
Determine whether the ordered pair is a solution of the system of linear equations
A) Yes
B) No
A) Yes
B) No

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
10
Solve the system of equations by the substitution method.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the system of equations by the substitution method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
12
Determine whether the ordered pair is a solution of the system of linear equations
A) Yes
B) No
A) Yes
B) No

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
13
Solve the system by graphing.
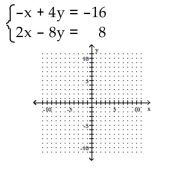
A) (-4, -1)
B) (0, -1)
C) (0, -4)
D)

A) (-4, -1)
B) (0, -1)
C) (0, -4)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
14
Solve the system of equations by the substitution method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
15
Determine whether the ordered pair is a solution of the system of linear equations
A) Yes
B) No
A) Yes
B) No

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
16
Solve the system of equations by the substitution method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
17
Determine whether the ordered pair is a solution of the system of linear equations
A) Yes
B) No
A) Yes
B) No

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
18
Solve the system of equations by the substitution method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the system of equations by the substitution method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
20
Determine whether the ordered pair is a solution of the system of linear equations
A) Yes
B) No
A) Yes
B) No

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
21
Solve the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
22
Solve the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
23
Solve the system of equations by the elimination method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
24
Solve the system of equations by the elimination method.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
25
Solve the system of equations by the elimination method.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
26
Solve the system of equations.
B)
A)
C)
D)
B)
A)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
28
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold
and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of
mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost
and revenue equations.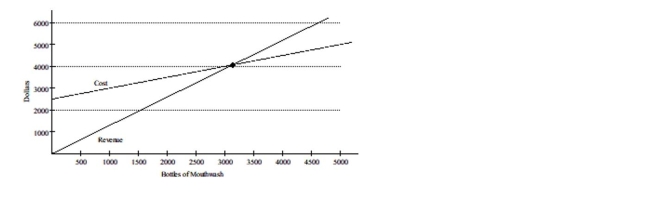
If the company sells 3000 bottles of mouthwash, does the company make money or lose money?
The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold
and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of
mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost
and revenue equations.

If the company sells 3000 bottles of mouthwash, does the company make money or lose money?

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
29
Solve the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
30
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold
and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of
mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost
and revenue equations.
Find the coordinates of the point of intersection, or breakeven point, by solving the system
and explain its meaning.
The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold
and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of
mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost
and revenue equations.

Find the coordinates of the point of intersection, or breakeven point, by solving the system
and explain its meaning.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the system of equations.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the system of equations by the elimination method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the system of equations by the elimination method.
B)
A)
D)
C)
B)
A)
D)
C)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
35
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold
and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of
mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost
and revenue equations.
If the company sells 3500 bottles of mouthwash, does the company make money or lose money?
The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold
and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of
mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost
and revenue equations.

If the company sells 3500 bottles of mouthwash, does the company make money or lose money?

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the system of equations.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
37
Solve the system of equations by the elimination method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
38
Solve the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
41
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold
and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of
mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost
and revenue equations.
For what x-values will the company lose money?
The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold
and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of
mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost
and revenue equations.

For what x-values will the company lose money?

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the system.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
43
Solve the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
44
Solve.
One number is 4 less than a second number. Twice the second number is 30 more than 4 times the first. Find the two numbers.
A) and
B) and
C) and
D) 7 and 11
One number is 4 less than a second number. Twice the second number is 30 more than 4 times the first. Find the two numbers.
A) and
B) and
C) and
D) 7 and 11

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the system.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
46
Solve.
One number is 3 less than a second number. Twice the second number is 21 less than 5 times the first. Find the two numbers.
A) 9 and 12
B) and
C) 10 and 13
D) 8 and 11
One number is 3 less than a second number. Twice the second number is 21 less than 5 times the first. Find the two numbers.
A) 9 and 12
B) and
C) 10 and 13
D) 8 and 11

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the system.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
52
Solve the system.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
53
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold
and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of
mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost
and revenue equations.
A)
В)
C)
D)
The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold
and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of
mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost
and revenue equations.

A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the system.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
56
Solve the system.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
57
Solve the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
58
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold
and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of
mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost
and revenue equations.
A)
B)
C)
D)
The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold
and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of
mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost
and revenue equations.

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
59
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold
and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of
mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost
and revenue equations.
For what x-values will the company make a profit?
The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold
and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of
mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost
and revenue equations.

For what x-values will the company make a profit?

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
61
Given the cost function, C(x), and the revenue function, R(x), find the number of units x that must be sold to break even.
A vendor sells hot dogs, bags of potato chips, and soft drinks. A customer buys 3 hot dogs, 3 bags of potato chips, and 3 soft drinks for $11.25. The price of a hot dog is $1.25 more than the price of a bag of potato chips.
The cost of a soft drink is $2.00 less than the price of two hot dogs. Find the cost of each item.
A) $2.00 for a hot dog; $0.75 for a bag of potato chips; $1.50 for a soft drink
B) $1.75 for a hot dog; $1.50 for a bag of potato chips; $0.50 for a soft drink
C) $0.50 for a hot dog; $1.75 for a bag of potato chips; $1.50 for a soft drink
D) $1.75 for a hot dog; $0.50 for a bag of potato chips; $1.50 for a soft drink
A vendor sells hot dogs, bags of potato chips, and soft drinks. A customer buys 3 hot dogs, 3 bags of potato chips, and 3 soft drinks for $11.25. The price of a hot dog is $1.25 more than the price of a bag of potato chips.
The cost of a soft drink is $2.00 less than the price of two hot dogs. Find the cost of each item.
A) $2.00 for a hot dog; $0.75 for a bag of potato chips; $1.50 for a soft drink
B) $1.75 for a hot dog; $1.50 for a bag of potato chips; $0.50 for a soft drink
C) $0.50 for a hot dog; $1.75 for a bag of potato chips; $1.50 for a soft drink
D) $1.75 for a hot dog; $0.50 for a bag of potato chips; $1.50 for a soft drink

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
62
Given the cost function, C(x), and the revenue function, R(x), find the number of units x that must be sold to break even.
A) 9 units
B) 3 units
C) 8 units
D) 7 units
A) 9 units
B) 3 units
C) 8 units
D) 7 units

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
63
Given the cost function, C(x), and the revenue function, R(x), find the number of units x that must be sold to break even.
A) 802 units
B) 800 units
C) 311 units
D) 801 units
A) 802 units
B) 800 units
C) 311 units
D) 801 units

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
64
Solve.
University Theater sold 562 tickets for a play. Tickets cost $23 per adult and $13 per senior citizen. If total receipts were $9086, how many senior citizen tickets were sold?
A) 178 senior citizen tickets
B) 294 senior citizen tickets
C) 268 senior citizen tickets
D) 384 senior citizen tickets
University Theater sold 562 tickets for a play. Tickets cost $23 per adult and $13 per senior citizen. If total receipts were $9086, how many senior citizen tickets were sold?
A) 178 senior citizen tickets
B) 294 senior citizen tickets
C) 268 senior citizen tickets
D) 384 senior citizen tickets

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
65
Solve.
The manager of a bulk foods establishment sells a trail mix for $5 per pound and premium cashews for $11 per pound. The manager wishes to make a 120-pound trail mix-cashew mixture that will sell for $9 per pound.
How many pounds of each should be used?
A) 100 pounds of trail mix
B) 60 pounds of trail mix 20 pounds of cashews 60 pounds of cashews
C) 80 pounds of trail mix
D) 40 pounds of trail mix 40 pounds of cashews 80 pounds of cashews
The manager of a bulk foods establishment sells a trail mix for $5 per pound and premium cashews for $11 per pound. The manager wishes to make a 120-pound trail mix-cashew mixture that will sell for $9 per pound.
How many pounds of each should be used?
A) 100 pounds of trail mix
B) 60 pounds of trail mix 20 pounds of cashews 60 pounds of cashews
C) 80 pounds of trail mix
D) 40 pounds of trail mix 40 pounds of cashews 80 pounds of cashews

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
66
Given the cost function, C(x), and the revenue function, R(x), find the number of units x that must be sold to break even.
A) 142 units
B) 141 units
C) 140 units
D) 22 units
A) 142 units
B) 141 units
C) 140 units
D) 22 units

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
67
Given the cost function, C(x), and the revenue function, R(x), find the number of units x that must be sold to break even.
Find the values of , and c such that the equation has ordered pair solutions , , and .
A)
B)
C)
D)
Find the values of , and c such that the equation has ordered pair solutions , , and .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
68
Solve.
A chemist needs 170 milliliters of a 59% solution but has only 15% and 83% solutions available. Find how many milliliters of each that should be mixed to get the desired solution.
A) 65 ml of 15%; 105 ml of 83%
B) 65 ml of 15%; 110 ml of 83%
C) 110 ml of 15%; 60 ml of 83%
D) 60 ml of 15%; 110 ml of 83%
A chemist needs 170 milliliters of a 59% solution but has only 15% and 83% solutions available. Find how many milliliters of each that should be mixed to get the desired solution.
A) 65 ml of 15%; 105 ml of 83%
B) 65 ml of 15%; 110 ml of 83%
C) 110 ml of 15%; 60 ml of 83%
D) 60 ml of 15%; 110 ml of 83%

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
69
Given the cost function, C(x), and the revenue function, R(x), find the number of units x that must be sold to break even.
At the break-even point both cost and revenue are what?
A) $1500
B) $2700
C) $750
D) $2250
At the break-even point both cost and revenue are what?
A) $1500
B) $2700
C) $750
D) $2250

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
70
Given the cost function, C(x), and the revenue function, R(x), find the number of units x that must be sold to break even.
A) 1120 units
B) 1110 units
C) 1100 units
D) 489 units
A) 1120 units
B) 1110 units
C) 1100 units
D) 489 units

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
71
Solve.
A certain aircraft can fly 1190 miles with the wind in 5 hours and travel the same distance against the wind in 7 hours. What is the speed of the wind?
A) 17 mph
B) 34 mph
C) 68 mph
D) 51 mph
A certain aircraft can fly 1190 miles with the wind in 5 hours and travel the same distance against the wind in 7 hours. What is the speed of the wind?
A) 17 mph
B) 34 mph
C) 68 mph
D) 51 mph

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
72
Solve.
A vendor sells hot dogs and bags of potato chips. A customer buys 5 hot dogs and 3 bags of potato chips for $9.25. Another customer buys 4 hot dogs and 5 bags of potato chips for $10.00. Find the cost of each item.
A) $1.25 for a hot dog; $1.25 for a bag of potato chips
B) $1.00 for a hot dog; $1.25 for a bag of potato chips
C) $1.50 for a hot dog; $1.25 for a bag of potato chips
D) $1.25 for a hot dog; $1.00 for a bag of potato chips
A vendor sells hot dogs and bags of potato chips. A customer buys 5 hot dogs and 3 bags of potato chips for $9.25. Another customer buys 4 hot dogs and 5 bags of potato chips for $10.00. Find the cost of each item.
A) $1.25 for a hot dog; $1.25 for a bag of potato chips
B) $1.00 for a hot dog; $1.25 for a bag of potato chips
C) $1.50 for a hot dog; $1.25 for a bag of potato chips
D) $1.25 for a hot dog; $1.00 for a bag of potato chips

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
73
Given the cost function, C(x), and the revenue function, R(x), find the number of units x that must be sold to break even.
A basketball player scored 16 points in a game. The number of three-point field goals the player made was 14 less than three times the number of free throws (each worth 1 point). Twice the number of two-point field goals
The player made was 7 more than the number of three-point field goals made. Find the number of free-throws,
Two-point field goals, and three-point field goals that the player made in the game.
A) 6 free throws; 4 two-point field goals; 4 three-point field goals
B) 5 free throws; 4 two-point field goals; 1 three-point field goals
C) 5 free throws; 5 two-point field goals; 3 three-point field goals
D) 5 free throws; 1 two-point field goals; 4 three-point field goals
A basketball player scored 16 points in a game. The number of three-point field goals the player made was 14 less than three times the number of free throws (each worth 1 point). Twice the number of two-point field goals
The player made was 7 more than the number of three-point field goals made. Find the number of free-throws,
Two-point field goals, and three-point field goals that the player made in the game.
A) 6 free throws; 4 two-point field goals; 4 three-point field goals
B) 5 free throws; 4 two-point field goals; 1 three-point field goals
C) 5 free throws; 5 two-point field goals; 3 three-point field goals
D) 5 free throws; 1 two-point field goals; 4 three-point field goals

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
74
Given the cost function, C(x), and the revenue function, R(x), find the number of units x that must be sold to break even.
A store sells tents, sleeping bags, and camp stools. A customer buys a tent, 4 sleeping bags, and 3 camp stools for $220. The price of the tent is 7 times the cost of a camp stool. The cost of a sleeping bag is $20 more than the
Cost of a camp stool. Find the cost of each item.
A) $77 for a tent; $30 for a sleeping bag; $11 for a camp stool
B) $70 for a tent; $35 for a sleeping bag; $15 for a camp stool
C) $70 for a tent; $30 for a sleeping bag; $10 for a camp stool
D) $70 for a tent; $30 for a sleeping bag; $11 for a camp stool
A store sells tents, sleeping bags, and camp stools. A customer buys a tent, 4 sleeping bags, and 3 camp stools for $220. The price of the tent is 7 times the cost of a camp stool. The cost of a sleeping bag is $20 more than the
Cost of a camp stool. Find the cost of each item.
A) $77 for a tent; $30 for a sleeping bag; $11 for a camp stool
B) $70 for a tent; $35 for a sleeping bag; $15 for a camp stool
C) $70 for a tent; $30 for a sleeping bag; $10 for a camp stool
D) $70 for a tent; $30 for a sleeping bag; $11 for a camp stool

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
75
Given the cost function, C(x), and the revenue function, R(x), find the number of units x that must be sold to break even.
Three trains one eastbound, one westbound, and one northbound leave a city at the same time. The speed of the northbound train is 10 miles per hour greater than the speed of the eastbound train. After 2 hours, the
Distance between the westbound train and the eastbound train is 200 miles. Twice the speed of the westbound
Train is 100 miles per hour more than the speed of the northbound train. Find the speeds of the three trains.
A) eastbound, 40 mph; westbound, 70 mph; northbound, 30 mph
B) eastbound, 20 mph; westbound, 80 mph; northbound, 40 mph
C) eastbound, 30 mph; westbound, 70 mph; northbound, 40 mph
D) eastbound, 40 mph; westbound, 70 mph; northbound, 50 mph
Three trains one eastbound, one westbound, and one northbound leave a city at the same time. The speed of the northbound train is 10 miles per hour greater than the speed of the eastbound train. After 2 hours, the
Distance between the westbound train and the eastbound train is 200 miles. Twice the speed of the westbound
Train is 100 miles per hour more than the speed of the northbound train. Find the speeds of the three trains.
A) eastbound, 40 mph; westbound, 70 mph; northbound, 30 mph
B) eastbound, 20 mph; westbound, 80 mph; northbound, 40 mph
C) eastbound, 30 mph; westbound, 70 mph; northbound, 40 mph
D) eastbound, 40 mph; westbound, 70 mph; northbound, 50 mph

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
76
Given the cost function, C(x), and the revenue function, R(x), find the number of units x that must be sold to break even.
Use the revenue and cost functions to write the profit function from producing and selling binoculars.
A)
B)
C)
D)
Use the revenue and cost functions to write the profit function from producing and selling binoculars.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
77
Given the cost function, C(x), and the revenue function, R(x), find the number of units x that must be sold to break even.
A) 1801 units
B) 1800 units
C) 634 units
D) 1802 units
A) 1801 units
B) 1800 units
C) 634 units
D) 1802 units

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
78
Given the cost function, C(x), and the revenue function, R(x), find the number of units x that must be sold to break even.
What is the profit when 796 binoculars are produced?
A) $3092
B) $92
C) $4684
D) $1684
What is the profit when 796 binoculars are produced?
A) $3092
B) $92
C) $4684
D) $1684

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
79
Solve.
Two cars leave a city and head in the same direction. After 5 hours, the faster car is 15 miles ahead of the slower car. The slower car has traveled 230 miles. Find the speeds of the two cars.
A) 30 mph and 33 mph
B) 46 mph and 49 mph
C) 43 mph and 46 mph
D) 48 mph and 51 mph
Two cars leave a city and head in the same direction. After 5 hours, the faster car is 15 miles ahead of the slower car. The slower car has traveled 230 miles. Find the speeds of the two cars.
A) 30 mph and 33 mph
B) 46 mph and 49 mph
C) 43 mph and 46 mph
D) 48 mph and 51 mph

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
80
Solve the system of linear equations using matrices.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck


