Exam 4: Systems of Equations and Inequalities

Fill in the blank with one of the words or phrases listed below. matrix consistent system of equations triple solution inconsistent element column -A(n) system of equations has at least one solution.

Solve the system. - $\left\{ \begin{array} { l } x - y + z = - 11 \\x + y + z = - 1 \\x + y - z = 1\end{array} \right.$

Solve the system of equations by the elimination method. - $\left\{ \begin{aligned}7 x + y & = 3 \\3 y & = 9 - 21 x\end{aligned} \right.$

Graph the solution of the system of linear inequalities. - $\left\{\begin{array}{r}3 x+3 y \leq 9 \\4 x+y \leq 5 \\x \geq 0 \\y \geq 0\end{array}\right.$

Given the cost function, C(x), and the revenue function, R(x), find the number of units x that must be sold to break even. -A basketball player scored 16 points in a game. The number of three-point field goals the player made was 14 less than three times the number of free throws (each worth 1 point). Twice the number of two-point field goals The player made was 7 more than the number of three-point field goals made. Find the number of free-throws, Two-point field goals, and three-point field goals that the player made in the game.

Write the word or phrase that best completes each statement or answers the question. The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost and revenue equations. 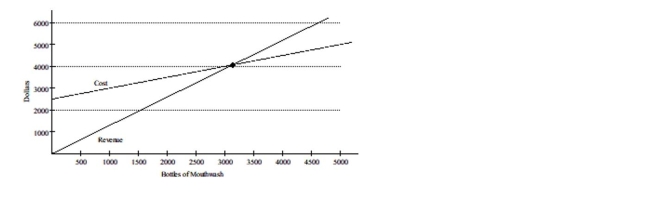-If the company sells 3000 bottles of mouthwash, does the company make money or lose money?

Graph the solution of the system of linear inequalities. - $\left\{\begin{array}{l}y<3 x-2 \\y \leq-3 x\end{array}\right.$

Determine whether the ordered pair is a solution of the system of linear equations $( 1 , - 3 ) , \left\{ \begin{array} { l } 2 x + y = - 1 \\4 x + 2 y = - 2\end{array} \right.$

Fill in the blank with one of the words or phrases listed below. matrix consistent system of equations triple solution inconsistent element column -A(n) system of equations has no solution.

Solve. -One number is 4 less than a second number. Twice the second number is 30 more than 4 times the first. Find the two numbers.

Solve the system of equations by the substitution method. - $\left\{ \begin{array} { r } x + 7 y = 35 \\- 4 x + 8 y = 40\end{array} \right.$

Graph the solution of the system of linear inequalities. - $\left\{\begin{array}{l}3 x+y<3 \\3 x+y>-1\end{array}\right.$

Solve the system of linear equations using matrices. - $\left\{ \begin{array} { l } 5 x + 5 y = 10 \\3 x - 2 y = - 24\end{array} \right.$

Graph the solution of the system of linear inequalities. - $\left\{\begin{array}{l}y \geq 2 x-1 \\y \leq 1-x\end{array}\right.$

Use matrices to solve the system. - $\left\{ \begin{array} { r r } 2 x - y - 9 z & = - 33 \\- 8 x - 3 z & = - 71 \\2 y + z & = 9\end{array} \right.$

Solve. -University Theater sold 562 tickets for a play. Tickets cost $23 per adult and $13 per senior citizen. If total receipts were $9086, how many senior citizen tickets were sold?

Solve the system. - $\left\{ \begin{array} { r } x + y + z = 6 \\x - y + 3 z = 10 \\2 x + 2 y + 2 z = 8\end{array} \right.$

Determine whether the ordered pair is a solution of the system of linear equations $( 3,3 ) , \left\{ \begin{array} { l } x + y = 0 \\x - y = - 6\end{array} \right.$

Solve the system of linear equations using matrices. - $\left\{ \begin{array} { r r } 2 x - 8 y - z = & - 20 \\x - 7 y + 6 z = & 17 \\6 x + y + z = & 64\end{array} \right.$

$\left\{\begin{array}{rr}6 x+y= & 0 \\-6 x+y= & -12\end{array}\right.$