Deck 7: Analytic Geometry
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/131
Play
Full screen (f)
Deck 7: Analytic Geometry
1
The line segment perpendicular to the major axis, with endpoints on the ellipse, and passing through
the center of the ellipse is called the axis.
the center of the ellipse is called the axis.
minor
2
The circle, the ellipse, the hyperbola, and the parabola are categories of sections.
conic
3
Graph the ellipse.
A)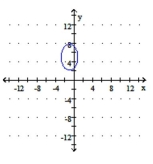
B)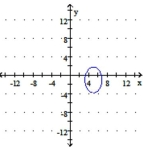 C )
C )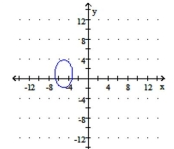
D)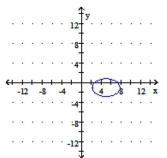
A)

B)
 C )
C )
D)

B
4
Graph the ellipse.
A)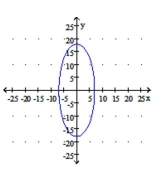
B)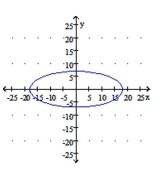 C)
C)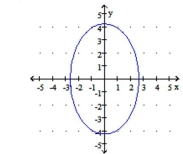
D)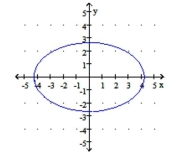
A)

B)
 C)
C)
D)


Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
5
The line segment with endpoints at the vertices of an ellipse is called the axis.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
6
The center of an ellipse is the midpoint of the axis.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
7
Choose the one alternative that best completes the statement or answers the question.
From the equation of the ellipse, determine if the major axis is horizontal or vertical.
A) Horizontal
B) Vertical
From the equation of the ellipse, determine if the major axis is horizontal or vertical.
A) Horizontal
B) Vertical

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
8
Given where > 0, the ordered pairs representing the endpoints of the
vertices are and . The ordered pairs representing the endpoints of the minor axis
are and .
vertices are and . The ordered pairs representing the endpoints of the minor axis
are and .

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
9
The line through the foci intersects an ellipse at two points called .

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
10
When referring to the standard form of an equation of an ellipse, the , e, is defined as

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
11
Graph the ellipse. Identify the foci and vertices.
A) foci: ;
vertices:
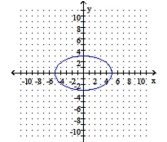
B) foci: ;
vertices:
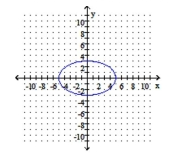 C) foci: ;
C) foci: ;
vertices:
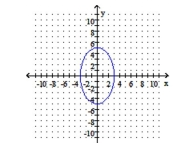
D) foci: ;
vertices:
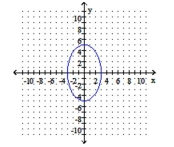
A) foci: ;
vertices:

B) foci: ;
vertices:
 C) foci: ;
C) foci: ;vertices:

D) foci: ;
vertices:


Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
12
Given where e ordered pairs representing the vertices are and
. The ordered pairs representing the endpoints of the minor axis are and
.
. The ordered pairs representing the endpoints of the minor axis are and
.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
13
Identify the vertices and the foci.
A) vertices: and ;
foci: and
B) vertices: and ;
foci: and
C) vertices: and
foci: and
D) vertices: and ;
foci: and
A) vertices: and ;
foci: and
B) vertices: and ;
foci: and
C) vertices: and
foci: and
D) vertices: and ;
foci: and

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
14
Given > 0, the ordered pairs representing the endpoints of the
vertices are and . The ordered pairs representing the endpoints of the minor axis
are and .
vertices are and . The ordered pairs representing the endpoints of the minor axis
are and .

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
15
The standard form of an equation of an ellipse centered at the origin with a horizontal major axis is
, where > 0. If the major axis is vertical, then the equation is .
, where > 0. If the major axis is vertical, then the equation is .

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
16
The standard form of an equation of an ellipse centered at (h, k) with a horizontal major axis is
, where > 0. If the major axis is vertical, then the equation is .
, where > 0. If the major axis is vertical, then the equation is .

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
17
Determine the length of the major and minor axis.
A) length of major axis: 18 ;
length of minor axis: 4
B) length of major axis: 81 ;
length of minor axis: 4
C) length of major axis: 2 ;
length of minor axis: 9
D) length of major axis: 9 ;
length of minor axis: 2
A) length of major axis: 18 ;
length of minor axis: 4
B) length of major axis: 81 ;
length of minor axis: 4
C) length of major axis: 2 ;
length of minor axis: 9
D) length of major axis: 9 ;
length of minor axis: 2

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
18
Graph the ellipse. Identify the center and vertices.
A) center: ;
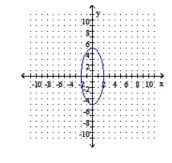
vertices
B) center: ;
vertices
11ecb0df_780a_ecd8_8acf_cdc1bd8e0cb3_TB7600_00 C) center: ;
vertices
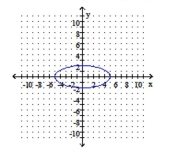
D) center: ;
vertices
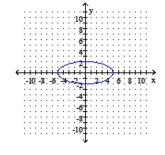
A) center: ;

vertices
B) center: ;
vertices
11ecb0df_780a_ecd8_8acf_cdc1bd8e0cb3_TB7600_00 C) center: ;
vertices

D) center: ;
vertices


Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
19
An is a set of points (x, y) in a plane such that the sum of the distances between (x, y) and
two fixed points called is a constant.
two fixed points called is a constant.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
20
Graph the ellipse. Identify the center and vertices.
A) center: ;
vertices
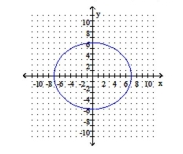
B) center: ;
vertices
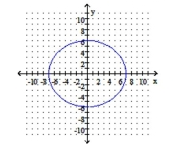 C) center: ;
C) center: ;
vertices
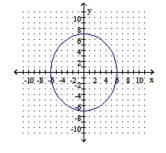
D) center: ;
vertices
11ecb0df_63be_6456_8acf_c38895cfdb3e_TB7600_00
A) center: ;
vertices

B) center: ;
vertices
 C) center: ;
C) center: ;vertices

D) center: ;
vertices
11ecb0df_63be_6456_8acf_c38895cfdb3e_TB7600_00

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
21
Write the equation of the ellipse in standard form. Identify the center and vertices.
A)
center: ; vertices:
B)
center: ; vertices:
C)
center: ; vertices:
D)
center: ; vertices:
A)
center: ; vertices:
B)
center: ; vertices:
C)
center: ; vertices:
D)
center: ; vertices:

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
22
Write the equation of the ellipse in standard form. Identify the vertices and foci.
A)
vertices:
foci
B)
vertices:
foci
C)
vertices:
foci
D)
vertices:
foci
A)
vertices:
foci
B)
vertices:
foci
C)
vertices:
foci
D)
vertices:
foci

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
23
Write the equation of the ellipse in standard form. Identify the vertices and foci.
A)
vertices:
foci:
B)
vertices:
foci:
C)
vertices:
foci:
D)
vertices:
foci:
A)
vertices:
foci:
B)
vertices:
foci:
C)
vertices:
foci:
D)
vertices:
foci:

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
24
Solve the problem.
A window above a door is to be made in the shape of a semiellipse. If the window is 12 feet at the base and 4 feet high at the center, determine the distance from the center at which the foci are
Located. Round to one decimal place.
A) 11.3 feet
B) 20.0 feet
C) 4.5 feet
D) 8.9 feet
A window above a door is to be made in the shape of a semiellipse. If the window is 12 feet at the base and 4 feet high at the center, determine the distance from the center at which the foci are
Located. Round to one decimal place.
A) 11.3 feet
B) 20.0 feet
C) 4.5 feet
D) 8.9 feet

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
25
Write the standard form of an equation of the ellipse subject to the given conditions.
Vertices: and
Foci: and
A)
B)
C)
D)
Vertices: and
Foci: and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
26
Write the standard form of an equation of the ellipse subject to the given conditions.
Vertices: and
Passes through
A)
B)
C)
D)
Vertices: and
Passes through
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
27
Determine the eccentricity of the ellipse.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
28
Write the standard form of an equation of the ellipse subject to the given conditions.
Foci: and
Length of minor axis: 4
A)
В)
C)
D)
Foci: and
Length of minor axis: 4
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
29
Write the equation of the ellipse in standard form. Identify the center and foci.
A)
center:
foci:
В)
center:
foci:
C)
center:
foci:
foci:
D)
center:
foci:
A)
center:
foci:
В)
center:
foci:
C)
center:
foci:
foci:
D)
center:
foci:

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
30
Graph the ellipse. Identify the center and the endpoints of the minor axis.
A) center: ;
endpts of minor axis:
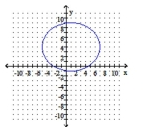
B) center: ;
endpts of minor axis:
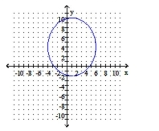 C) center: ;
C) center: ;
endpts of minor axis:
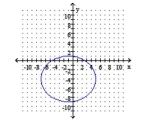
D) center: ;
endpts of minor axis:
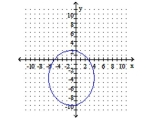
A) center: ;
endpts of minor axis:

B) center: ;
endpts of minor axis:
 C) center: ;
C) center: ;endpts of minor axis:

D) center: ;
endpts of minor axis:


Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
31
Write the standard form of an equation of the ellipse subject to the given conditions.
Vertices:
Foci:
A)
B)
C)
D)
Vertices:
Foci:
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the problem.
The reflective property of an ellipse is used in lithotripsy. Lithotripsy is a technique for treating kidney stones without surgery. Instead, high-energy shock waves are emitted from one focus of an
Elliptical shell and reflected painlessly to a patient's kidney stone located at the other focus. The
Vibration from the shock waves shatters the stone into pieces small enough to pass through the
Patient's urine.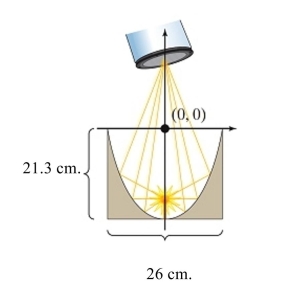 A vertical cross section of a lithotripter is in the shape of a semiellipse with the dimensions shown.
A vertical cross section of a lithotripter is in the shape of a semiellipse with the dimensions shown.
Approximate the distance from the center along the major axis where the patient's kidney stone should be
Located so the shock waves will target the stone. Round to two decimal places.
A) 16.87 cm. below the center
B) 24.95 cm. below the center
C) 14.91 cm. below the center
D) 40.57 cm. below the center
The reflective property of an ellipse is used in lithotripsy. Lithotripsy is a technique for treating kidney stones without surgery. Instead, high-energy shock waves are emitted from one focus of an
Elliptical shell and reflected painlessly to a patient's kidney stone located at the other focus. The
Vibration from the shock waves shatters the stone into pieces small enough to pass through the
Patient's urine.
 A vertical cross section of a lithotripter is in the shape of a semiellipse with the dimensions shown.
A vertical cross section of a lithotripter is in the shape of a semiellipse with the dimensions shown.Approximate the distance from the center along the major axis where the patient's kidney stone should be
Located so the shock waves will target the stone. Round to two decimal places.
A) 16.87 cm. below the center
B) 24.95 cm. below the center
C) 14.91 cm. below the center
D) 40.57 cm. below the center

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
33
Identify the center of the ellipse and the foci.
A) center: ;
foci: and
B) center: ;
foci: and
C) center: ;
foci: and
D) center: ;
foci: and
A) center: ;
foci: and
B) center: ;
foci: and
C) center: ;
foci: and
D) center: ;
foci: and

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
34
Write the standard form of an equation of the ellipse subject to the given conditions.
Endpoints of minor axis: and
Foci: and
A)
В)
C)
D)
Endpoints of minor axis: and
Foci: and
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
35
Identify the vertices and the foci.
A) vertices: and ;
foci: and
B) vertices: and ;
foci: and
C) vertices: and ;
foci: and
D) vertices: and ;
foci: and
A) vertices: and ;
foci: and
B) vertices: and ;
foci: and
C) vertices: and ;
foci: and
D) vertices: and ;
foci: and

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the problem.
The reflective property of an ellipse is the principle behind "whispering galleries". These are rooms with elliptically shaped ceilings such that a person standing at one focus can hear even the slightest whisper spoken
By another person standing at the other focus.
Suppose that a dome has a semielliptical ceiling, 94 ft long and 22 ft high. Approximately how far from
The center along the major axis should each person be standing to hear the "whispering" effect?
Round to one decimal place.
A) 25.0 feet
B) 41.5 feet
C) 91.4 feet
D) 51.9 feet
The reflective property of an ellipse is the principle behind "whispering galleries". These are rooms with elliptically shaped ceilings such that a person standing at one focus can hear even the slightest whisper spoken
By another person standing at the other focus.
Suppose that a dome has a semielliptical ceiling, 94 ft long and 22 ft high. Approximately how far from
The center along the major axis should each person be standing to hear the "whispering" effect?
Round to one decimal place.
A) 25.0 feet
B) 41.5 feet
C) 91.4 feet
D) 51.9 feet

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
37
Graph the ellipse. Identify the foci and vertices.
A) foci: ;
vertices:
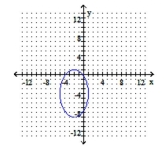
B) foci: ;
vertices:
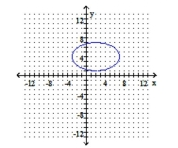 C) foci: ;
C) foci: ;
vertices:
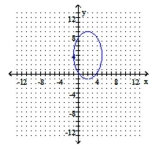
D) foci: ;
vertices:
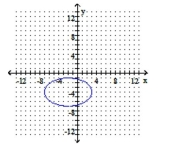
A) foci: ;
vertices:

B) foci: ;
vertices:
 C) foci: ;
C) foci: ;vertices:

D) foci: ;
vertices:


Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
38
Solve the problem.
A homeowner wants to make an elliptical rug from a 30-foot by 10-foot rectangular piece of carpeting. a. What lengths of the major and minor axes would maximize the area of the new rug?
B) Write an equation of the ellipse with maximum area. Use a coordinate system with the origin at the center
Of the rug and horizontal major axis. A) a. Major axis: 32 feet. Minor axis: 16 feet
b.
B) a. Major axis: 15 feet. Minor axis: 5 feet
b.
C) a. Major axis: 30 feet. Minor axis: 10 feet
b.
D) a. Major axis: 30 feet. Minor axis: 10 feet
b.
A homeowner wants to make an elliptical rug from a 30-foot by 10-foot rectangular piece of carpeting. a. What lengths of the major and minor axes would maximize the area of the new rug?
B) Write an equation of the ellipse with maximum area. Use a coordinate system with the origin at the center
Of the rug and horizontal major axis. A) a. Major axis: 32 feet. Minor axis: 16 feet
b.
B) a. Major axis: 15 feet. Minor axis: 5 feet
b.
C) a. Major axis: 30 feet. Minor axis: 10 feet
b.
D) a. Major axis: 30 feet. Minor axis: 10 feet
b.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
39
Write the equation of the ellipse in standard form. Identify the vertices and foci.
A)
vertices:
foci
B)
vertices:
foci
C)
vertices:
foci
D)
vertices:
foci
A)
vertices:
foci
B)
vertices:
foci
C)
vertices:
foci
D)
vertices:
foci

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
40
Determine the eccentricity of the ellipse.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
41
Graph the hyperbola. Identify the center and vertices.
A) center: ;
vertices:
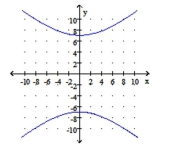
B) center: ;
vertices:
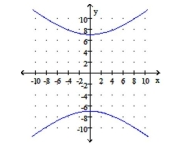 C) center: ;
C) center: ;
vertices:
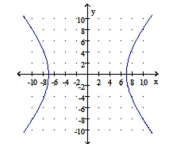
D) center: ;
vertices:
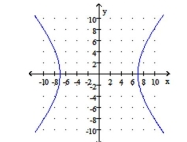
A) center: ;
vertices:

B) center: ;
vertices:
 C) center: ;
C) center: ;vertices:

D) center: ;
vertices:


Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
42
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
The points where a hyperbola intersects the line through the foci are called the .
Provide the missing information.
The points where a hyperbola intersects the line through the foci are called the .

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
43
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
The equation = 1 represents a hyperbola with a (horizontal / vertical) transverse axis. The
vertices are given by the ordered pairs and . The asymptotes are given by the
equations and .
Provide the missing information.
The equation = 1 represents a hyperbola with a (horizontal / vertical) transverse axis. The
vertices are given by the ordered pairs and . The asymptotes are given by the
equations and .

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
44
Given an ellipse with major axis of length 2a and minor axis of length 2b, the area is given by A =ab.
The perimeter is approximated by a. Determine the area of the ellipse. b. Approximate the perimeter.
A) a. square units
b. units
B) a. square units
b. units
C) a. square units
b. units
D) a. square units
b. units
The perimeter is approximated by a. Determine the area of the ellipse. b. Approximate the perimeter.
A) a. square units
b. units
B) a. square units
b. units
C) a. square units
b. units
D) a. square units
b. units

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
45
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
Given e ordered pairs representing the vertices are and .
Provide the missing information.
Given e ordered pairs representing the vertices are and .

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
46
Write the standard form of an equation of the ellipse subject to the given conditions.
Foci: and Eccentricity:
A)
B)
C)
D)
Foci: and Eccentricity:
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
47
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
Given e ordered pairs representing the vertices are and .
Provide the missing information.
Given e ordered pairs representing the vertices are and .

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the problem.
A planet's moon has an orbit that is elliptical with eccentricity 0.054 and with the planet at one focus. If the distance between the moon and the planet at perihelion (the closest point) is 364,100
Km, determine the distance at aphelion (the farthest point). Round to the nearest 100 km.
A) 384,900 km
B) 769,800 km
C) 749,000 km
D) 405,700 km
A planet's moon has an orbit that is elliptical with eccentricity 0.054 and with the planet at one focus. If the distance between the moon and the planet at perihelion (the closest point) is 364,100
Km, determine the distance at aphelion (the farthest point). Round to the nearest 100 km.
A) 384,900 km
B) 769,800 km
C) 749,000 km
D) 405,700 km

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
49
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
The equation = 1 represents a hyperbola with a (horizontal / vertical) transverse axis. The
vertices are given by the ordered pairs and . The asymptotes are given by the
equations and .
Provide the missing information.
The equation = 1 represents a hyperbola with a (horizontal / vertical) transverse axis. The
vertices are given by the ordered pairs and . The asymptotes are given by the
equations and .

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the problem.
a. A circular vent pipe with diameter 4 inches is placed on a flat roof. Write an equation of the circular cross section that the pipe makes with the roof. Assume the origin is placed at the center of
The circle.
B) Suppose the pipe is instead placed on a roof with a slope of . The cross-section of the pipe
Where it intersects the roof is an ellipse. Determine the lengths of the major and minor axes of this
Ellipse. A) a.
b. Major axis in; minor axis in
B) a.
b. Major axis in; minor axis in
C) a.
b. Major axis in; minor axis in
D) a.
b. Major axis in; minor axis in
a. A circular vent pipe with diameter 4 inches is placed on a flat roof. Write an equation of the circular cross section that the pipe makes with the roof. Assume the origin is placed at the center of
The circle.
B) Suppose the pipe is instead placed on a roof with a slope of . The cross-section of the pipe
Where it intersects the roof is an ellipse. Determine the lengths of the major and minor axes of this
Ellipse. A) a.
b. Major axis in; minor axis in
B) a.
b. Major axis in; minor axis in
C) a.
b. Major axis in; minor axis in
D) a.
b. Major axis in; minor axis in

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
51
Choose the one alternative that best completes the statement or answers the question.
Determine whether the transverse axis and foci of the hyperbola are on the x-axis or the y-axis.
A) -axis
B) -axis
Determine whether the transverse axis and foci of the hyperbola are on the x-axis or the y-axis.
A) -axis
B) -axis

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
52
Solve the problem.
A park has an elliptical shape with a major axis of 970 feet and a minor axis of 917 feet. Find the equation of the elliptical boundary.
A) Take the horizontal axis to be the major axis and locate the origin of the coordinate system at the
Center of the ellipse.
B) Approximate the eccentricity of the ellipse. Round to two decimal places. A) a.
b.
В)
b.
C) a.
b.
D) a.
b.
A park has an elliptical shape with a major axis of 970 feet and a minor axis of 917 feet. Find the equation of the elliptical boundary.
A) Take the horizontal axis to be the major axis and locate the origin of the coordinate system at the
Center of the ellipse.
B) Approximate the eccentricity of the ellipse. Round to two decimal places. A) a.
b.
В)
b.
C) a.
b.
D) a.
b.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
53
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
A is the set of point (x, y) in a plane such that the difference in distances between (x, y)
and two fixed points (called ) is a positive constant.
Provide the missing information.
A is the set of point (x, y) in a plane such that the difference in distances between (x, y)
and two fixed points (called ) is a positive constant.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
54
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
The line segment perpendicular to the transverse axis passing through the center of a hyperbola, and
with endpoints on the reference rectangle is called the axis.
Provide the missing information.
The line segment perpendicular to the transverse axis passing through the center of a hyperbola, and
with endpoints on the reference rectangle is called the axis.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
55
Write the standard form of an equation of the ellipse subject to the given conditions.
Center ; Eccentricity: ; Major axis vertical of length 50 units
A)
B)
C)
D)
Center ; Eccentricity: ; Major axis vertical of length 50 units
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
56
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
When referring to the standard form of an equation of a hyperbola, the , e, is defined as e
Provide the missing information.
When referring to the standard form of an equation of a hyperbola, the , e, is defined as e

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
57
Solve the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
58
Solve the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
59
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
The midpoint of the transverse axis is the of the hyperbola.
Provide the missing information.
The midpoint of the transverse axis is the of the hyperbola.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
60
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
The line segment between the vertices of a hyperbola is called the axis.
Provide the missing information.
The line segment between the vertices of a hyperbola is called the axis.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
61
Identify the vertices and the foci.
A) vertices:
foci:
B) vertices:
foci:
C) vertices:
foci:
D) vertices:
foci:
A) vertices:
foci:
B) vertices:
foci:
C) vertices:
foci:
D) vertices:
foci:

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
62
Determine the eccentricity of the hyperbola.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
63
Write the equation of the hyperbola in standard form. Identify the center and vertices.
A)
center:
vertices: and
B)
center:
vertices: and
C)
center:
vertices: and
D)
center:
vertices: and
A)
center:
vertices: and
B)
center:
vertices: and
C)
center:
vertices: and
D)
center:
vertices: and

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
64
Write the standard form of the equation of the hyperbola subject to the given conditions.
Vertices: ; Foci
A)
B)
C)
D)
Vertices: ; Foci
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
65
Graph the hyperbola. Identify the foci and write the equations for the asymptotes.
A) foci: ;
asymptotes:
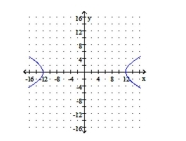
B) foci: ;
asymptotes:
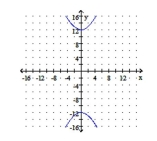 C) foci: ;
C) foci: ;
asymptotes:
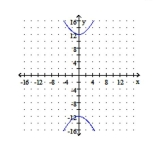
D) foci: ;
asymptotes:
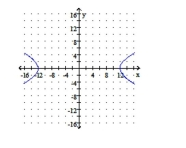
A) foci: ;
asymptotes:

B) foci: ;
asymptotes:
 C) foci: ;
C) foci: ;asymptotes:

D) foci: ;
asymptotes:


Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
66
Write the standard form of the equation of the hyperbola subject to the given conditions.
Corners of the reference rectangle: ; Horizontal transverse axis
A)
В)
C)
D)
Corners of the reference rectangle: ; Horizontal transverse axis
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
67
Write the standard form of the equation of the hyperbola subject to the given conditions.
Vertices:
Slope of the asymptotes:
A)
B)
C)
D)
Vertices:
Slope of the asymptotes:
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
68
Write the equation of the hyperbola in standard form. Identify the center and vertices.
A)
center: ; vertices:
B)
center: ; vertices:
C)
center: ; vertices:
D)
center: ; vertices:
A)
center: ; vertices:
B)
center: ; vertices:
C)
center: ; vertices:
D)
center: ; vertices:

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
69
Identify the foci and write equations for the asymptotes.
A) foci:
asymptotes: and
B) foci:
asymptotes: and
C) foci:
asymptotes: and
D) foci:
asymptotes: and
A) foci:
asymptotes: and
B) foci:
asymptotes: and
C) foci:
asymptotes: and
D) foci:
asymptotes: and

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
70
Write the equation of the hyperbola in standard form. Identify the center and foci.
A)
center:
foci:
В)
center:
foci:
C)
center:
foci:
D)
center:
foci:
A)
center:
foci:
В)
center:
foci:
C)
center:
foci:
D)
center:
foci:

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
71
Solve the problem.
Suppose that two microphones 2,800 m apart at points A = (1,400, 0) and B = (-1,400, 0) detect the sound of a rifle shot. The time difference between the sound detected at A and the sound detected at
B is 2 sec. If sound travels at approximately 330 m/sec, find an equation of the hyperbola with foci
At A and B defining the points where the shooter may be located. A)
B)
C)
D)
Suppose that two microphones 2,800 m apart at points A = (1,400, 0) and B = (-1,400, 0) detect the sound of a rifle shot. The time difference between the sound detected at A and the sound detected at
B is 2 sec. If sound travels at approximately 330 m/sec, find an equation of the hyperbola with foci
At A and B defining the points where the shooter may be located. A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
72
Solve the problem.
The cross section of a cooling tower of a nuclear power plant is in the shape of a hyperbola, and can be modeled by the equation where x and y are measured in meters. The base of the tower is located at y = 0, and the top of the
Tower is 110 m above the base. Determine the diameter of the tower at the top. Round to the nearest
Meter.
A) 55 m
B) 48 m
C) 28 m
D) 96 m
The cross section of a cooling tower of a nuclear power plant is in the shape of a hyperbola, and can be modeled by the equation where x and y are measured in meters. The base of the tower is located at y = 0, and the top of the
Tower is 110 m above the base. Determine the diameter of the tower at the top. Round to the nearest
Meter.
A) 55 m
B) 48 m
C) 28 m
D) 96 m

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
73
Determine the eccentricity of the hyperbola.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
74
Graph the hyperbola. Identify the foci and write the equations for the asymptotes.
A) foci: ; asymptotes:
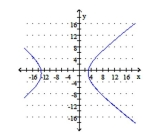
B) foci: ; asymptotes:
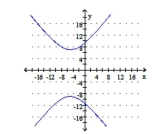 C) foci: ; asymptotes:
C) foci: ; asymptotes:
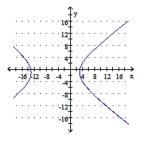
D) foci: ; asymptotes:
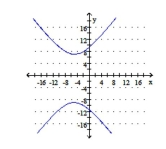
A) foci: ; asymptotes:

B) foci: ; asymptotes:
 C) foci: ; asymptotes:
C) foci: ; asymptotes:
D) foci: ; asymptotes:


Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
75
Write the standard form of the equation of the hyperbola subject to the given conditions.
Vertices: ; Foci:
A)
B)
C)
D)
Vertices: ; Foci:
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
76
Identify the vertices and the foci.
A) vertices:
foci:
B) vertices:
foci:
C) vertices:
foci:
D) vertices:
foci:
A) vertices:
foci:
B) vertices:
foci:
C) vertices:
foci:
D) vertices:
foci:

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
77
Write the standard form of the equation of the hyperbola subject to the given conditions.
Vertices: eccentricity
A)
B)
C)
D)
Vertices: eccentricity
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
78
Graph the hyperbola. Identify the center and vertices.
A) center: ;
vertices:
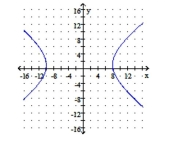
B) center: ;
vertices:
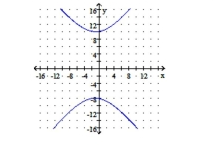 C) center: ;
C) center: ;
vertices:
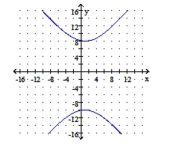
D) center: ;
vertices:
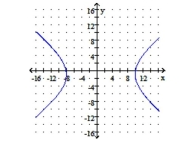
A) center: ;
vertices:

B) center: ;
vertices:
 C) center: ;
C) center: ;vertices:

D) center: ;
vertices:


Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
79
Write the standard form of the equation of the hyperbola subject to the given conditions.
Vertices: (0, -6), (0, 6); Asymptotes:
A)
B)
C)
D)
Vertices: (0, -6), (0, 6); Asymptotes:
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
80
Identify the vertices and the foci, and write equations for the asymptotes.
A) vertices:
foci:
asymptotes: and
B) vertices:
foci:
asymptotes: and
C) vertices:
foci:
asymptotes: and
D) vertices:
foci:
asymptotes: and
A) vertices:
foci:
asymptotes: and
B) vertices:
foci:
asymptotes: and
C) vertices:
foci:
asymptotes: and
D) vertices:
foci:
asymptotes: and

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck


