Deck 9: Matrices and Determinants
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/152
Play
Full screen (f)
Deck 9: Matrices and Determinants
1
Use Matrices and Gaussian Elimination to Solve Systems
A)
B)
C)
D)
A)
B)
C)
D)
A
2
Write the system of linear equations represented by the augmented matrix. Use x, y, z, and, if necessary, w for the variables. Then use back-substitution to find the solution.
A)
В)
C)
D)
A)
В)
C)
D)
A
3
Perform Matrix Row Operations
A)
B)
C)
D)
A)
B)
C)
D)
A
4
Simplify Complex Rational Expressions
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
5
Simplify Complex Rational Expressions
A)
B)
C)
A)
B)
C)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
6
Write the system of linear equations represented by the augmented matrix. Use x, y, z, and, if necessary, w for the variables.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
7
Use Matrices and Gauss-Jordan Elimination to Solve Systems
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
8
Use Matrices and Gaussian Elimination to Solve Systems
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
9
Write the system of linear equations represented by the augmented matrix. Use x, y, z, and, if necessary, w for the variables. Then use back-substitution to find the solution.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
10
Use Matrices and Gauss-Jordan Elimination to Solve Systems
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
11
Perform Matrix Row Operations
A)
B)
C)
A)
B)
C)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
12
Use Matrices and Gauss-Jordan Elimination to Solve Systems
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
13
Write the system of linear equations represented by the augmented matrix. Use x, y, z, and, if necessary, w for the variables. Then use back-substitution to find the solution.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
14
Simplify Complex Rational Expressions
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
15
Write the system of linear equations represented by the augmented matrix. Use x, y, z, and, if necessary, w for the variables.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
16
Use Matrices and Gaussian Elimination to Solve Systems
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
17
Perform Matrix Row Operations
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
18
Use Matrices and Gaussian Elimination to Solve Systems
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
19
Simplify Complex Rational Expressions
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
20
Use Matrices and Gaussian Elimination to Solve Systems
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
21
Use Matrices and Gauss-Jordan Elimination to Solve Systems
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
22
Inconsistent and Dependent Systems and Their Applications
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
23
Inconsistent and Dependent Systems and Their Applications
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
В)
C)
D)
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
24
Apply Gaussian Elimination to Systems with More Variables than Equations
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
25
Write a system of linear equations in three variables, and then use matrices to solve the system.
Ron attends a cocktail party (with his graphing calculator in his pocket). He wants to limit his food intake to 103 g protein, 93 g fat, and 135 g carbohydrate. According to the health conscious hostess, the marinated mushroom caps have 3 g protein, 5 g fat, and 9 g carbohydrate; the spicy meatballs have 14 g protein, 7 g fat, and 15 g carbohydrate; and the deviled eggs have 13 g protein, 15 g fat, and 6 g carbohydrate. How many of each snack can he eat to obtain his goal?
A) 7 mushrooms; 4 meatballs; 2 eggs
B) 4 mushrooms; 2 meatballs; 7 eggs
C) 2 mushrooms; 7 meatballs; 4 eggs
D) 8 mushrooms; 5 meatballs; 3 eggs
Ron attends a cocktail party (with his graphing calculator in his pocket). He wants to limit his food intake to 103 g protein, 93 g fat, and 135 g carbohydrate. According to the health conscious hostess, the marinated mushroom caps have 3 g protein, 5 g fat, and 9 g carbohydrate; the spicy meatballs have 14 g protein, 7 g fat, and 15 g carbohydrate; and the deviled eggs have 13 g protein, 15 g fat, and 6 g carbohydrate. How many of each snack can he eat to obtain his goal?
A) 7 mushrooms; 4 meatballs; 2 eggs
B) 4 mushrooms; 2 meatballs; 7 eggs
C) 2 mushrooms; 7 meatballs; 4 eggs
D) 8 mushrooms; 5 meatballs; 3 eggs

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
26
Inconsistent and Dependent Systems and Their Applications
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
27
Inconsistent and Dependent Systems and Their Applications
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
28
Inconsistent and Dependent Systems and Their Applications
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
29
Inconsistent and Dependent Systems and Their Applications
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
30
Write a system of linear equations in three variables, and then use matrices to solve the system.
A ceramics workshop makes wreaths, trees, and sleighs for sale at Christmas. A wreath takes 3 hours to prepare, 2 hours to paint, and 10 hours to fire. A tree takes 14 hours to prepare, 3 hours to paint, and 4 hours to fire. A sleigh takes 4 hours to prepare, 15 hours to paint, and 7 hours to fire. If the workshop has 85 hours for prep time, 56 hours for painting, and 100 hours for firing, how many of each can be made?
A) 7 wreaths; 4 trees; 2 sleighs
B) 4 wreaths; 2 trees; 7 sleighs
C) 2 wreaths; 7 trees; 4 sleighs
D) 8 wreaths; 5 trees; 3 sleighs
A ceramics workshop makes wreaths, trees, and sleighs for sale at Christmas. A wreath takes 3 hours to prepare, 2 hours to paint, and 10 hours to fire. A tree takes 14 hours to prepare, 3 hours to paint, and 4 hours to fire. A sleigh takes 4 hours to prepare, 15 hours to paint, and 7 hours to fire. If the workshop has 85 hours for prep time, 56 hours for painting, and 100 hours for firing, how many of each can be made?
A) 7 wreaths; 4 trees; 2 sleighs
B) 4 wreaths; 2 trees; 7 sleighs
C) 2 wreaths; 7 trees; 4 sleighs
D) 8 wreaths; 5 trees; 3 sleighs

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
31
Write a system of linear equations in three variables, and then use matrices to solve the system.
There were approximately 100,000 vehicles sold at a particular dealership last year. The dealer tracks sales by age group for marketing purposes. The percentage of 36- to 59-year-old buyers and the percentage of buyers 60 and older combined exceeds the percentage of buyers 35 and younger by 40%. If the percentage of buyers in the oldest group is doubled, it is 34% less than the percentage of users in the middle group. Find the percentage of buyers in each of the three age groups.
A) 30% 35 and younger; 58% 36-59 year olds; 12% 60 and older
B) 32% 35 and younger; 55% 36-59 year olds; 13% 60 and older
C) 24% 35 and younger; 60% 36-59 year olds; 16% 60 and older
D) 12% 35 and younger; 58% 36-59 year olds; 30% 60 and older
There were approximately 100,000 vehicles sold at a particular dealership last year. The dealer tracks sales by age group for marketing purposes. The percentage of 36- to 59-year-old buyers and the percentage of buyers 60 and older combined exceeds the percentage of buyers 35 and younger by 40%. If the percentage of buyers in the oldest group is doubled, it is 34% less than the percentage of users in the middle group. Find the percentage of buyers in each of the three age groups.
A) 30% 35 and younger; 58% 36-59 year olds; 12% 60 and older
B) 32% 35 and younger; 55% 36-59 year olds; 13% 60 and older
C) 24% 35 and younger; 60% 36-59 year olds; 16% 60 and older
D) 12% 35 and younger; 58% 36-59 year olds; 30% 60 and older

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
32
Inconsistent and Dependent Systems and Their Applications
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
33
Apply Gaussian Elimination to Systems with More Variables than Equations
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
34
Apply Gaussian Elimination to Systems with More Variables than Equations
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
35
Inconsistent and Dependent Systems and Their Applications
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
36
Apply Gaussian Elimination to Systems with More Variables than Equations
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
37
Inconsistent and Dependent Systems and Their Applications
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
38
Use Matrices and Gauss-Jordan Elimination to Solve Systems
A)
B)
C)
D) -
A)
B)
C)
D) -

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
39
Inconsistent and Dependent Systems and Their Applications
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)
1 Apply Gaussian Elimination to Systems Without Unique Solutions
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
40
Write a system of linear equations in three variables, and then use matrices to solve the system.
The table below shows the number of birds for three selected years after an endangered species protection program was started. Use the quadratic function to model the data. Solve the system of linear equations involving , and using matrices. Find the equation that models the data.
A)
B)
C)
D)
The table below shows the number of birds for three selected years after an endangered species protection program was started. Use the quadratic function to model the data. Solve the system of linear equations involving , and using matrices. Find the equation that models the data.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
41
Perform Scalar Multiplication
Let . Find 4A.
A)
B)
C)
D)
Let . Find 4A.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
42
Add and Subtract Matrices
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
43
Understand What is Meant by Equal Matrices
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
44
Understand What is Meant by Equal Matrices
B)
A)
D)
C)
B)
A)
D)
C)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
45
Understand What is Meant by Equal Matrices
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
46
Matrix Operations and Their Applications
1 Use Matrix Notation
A)
B)
C)
D)
1 Use Matrix Notation
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
47
Apply Gaussian Elimination to Systems with More Variables than Equations
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
48
Perform Scalar Multiplication
Let . Find .
A) ]
B) ]
C)
D)
Let . Find .
A) ]
B) ]
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
49
Perform Scalar Multiplication
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
50
Add and Subtract Matrices
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
51
Add and Subtract Matrices
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
52
Add and Subtract Matrices
Let and . Find
A)
B)
C)
D)
Let and . Find
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
53
Add and Subtract Matrices
A)
A)
B)
C)
D)
A)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
54
Solve Problems Involving Systems Without Unique Solutions
The figure below shows the intersection of three one-way streets. To keep traffic moving, the number of cars per minute entering an intersection must equal the number of cars leaving that intersection. Set up a system of equations that keeps traffic moving, and use Gaussian elimination to solve the system. If construction limits z to t cars per minute, how many cars per minute must pass through the other intersections to keep traffic moving?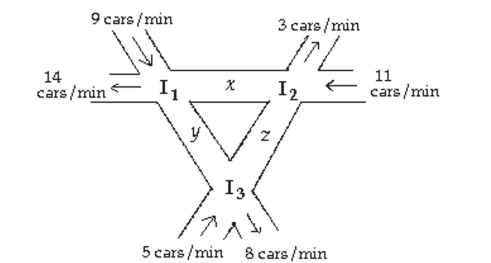
A) cars/min between and cars/min between and
B) cars/min between and cars/min between and
C) cars/min between and cars/min between and
D) cars between and cars/min between and
The figure below shows the intersection of three one-way streets. To keep traffic moving, the number of cars per minute entering an intersection must equal the number of cars leaving that intersection. Set up a system of equations that keeps traffic moving, and use Gaussian elimination to solve the system. If construction limits z to t cars per minute, how many cars per minute must pass through the other intersections to keep traffic moving?

A) cars/min between and cars/min between and
B) cars/min between and cars/min between and
C) cars/min between and cars/min between and
D) cars between and cars/min between and

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
55
Matrix Operations and Their Applications
1 Use Matrix Notation
A)
B)
C)
D)
1 Use Matrix Notation
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
56
Understand What is Meant by Equal Matrices
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
57
Solve Problems Involving Systems Without Unique Solutions
The nutritional content per ounce for three foods is given in the table below.
What combination of these foods can provide exactly 14 grams of fat, 27 grams of protein, and 10 grams of fiber?
A) No possible combination of these foods
B) of Food A; of Food B; of Food
C) 7 oz of Food A; 7 oz of Food B; 1 oz of Food
D) of Food of Food B; of Food
The nutritional content per ounce for three foods is given in the table below.
What combination of these foods can provide exactly 14 grams of fat, 27 grams of protein, and 10 grams of fiber?
A) No possible combination of these foods
B) of Food A; of Food B; of Food
C) 7 oz of Food A; 7 oz of Food B; 1 oz of Food
D) of Food of Food B; of Food

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
58
Add and Subtract Matrices
Let and . Find
A)
B)
C)
D)
Let and . Find
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
59
Add and Subtract Matrices
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
60
Solve Problems Involving Systems Without Unique Solutions
A company that manufactures products A, B, and C does both assembly and testing. The hours needed to assemble and test each product are shown in the table below.
The company has exactly 27 hours per week available for assembly and 120 hours per week available for testing. If the company must produce units of Product this week, how many units of Products and can they produce?
A) 15 of Product A; of Product B
B) 15 t of Product A; of Product
C) of Product of Product
D) 15 of Product A; 12 of Product B
A company that manufactures products A, B, and C does both assembly and testing. The hours needed to assemble and test each product are shown in the table below.
The company has exactly 27 hours per week available for assembly and 120 hours per week available for testing. If the company must produce units of Product this week, how many units of Products and can they produce?
A) 15 of Product A; of Product B
B) 15 t of Product A; of Product
C) of Product of Product
D) 15 of Product A; 12 of Product B

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
61
Solve Matrix Equations
Let and
A)
B)
C)
D)
Let and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
62
Multiply Matrices
A) is not defined.
B)
C)
D)
A) is not defined.
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
63
Solve Matrix Equations
Let and
A)
B)
C)
D)
Let and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
64
Multiply Matrices
A)
B) is not defined.
C) [
D)
A)
B) is not defined.
C) [
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
65
Multiply Matrices
A)
B) is not defined.
C)
D)
A)
B) is not defined.
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
66
Perform Scalar Multiplication
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
67
Solve Matrix Equations
Let and
A)
B)
C)
D)
Let and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
68
Multiply Matrices
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
69
Solve Matrix Equations
Let and
A)
B)
C)
D)
Let and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
70
Model Applied Situations with Matrix Operations
Adjust the contrast by changing the black to dark grey and the light grey to white. Use matrix addition to accomplish this. A)
B)
C)
D)
Adjust the contrast by changing the black to dark grey and the light grey to white. Use matrix addition to accomplish this. A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
71
Multiply Matrices
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
72
Multiply Matrices
A)
B) is not defined.
C)
D)
A)
B) is not defined.
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
73
Multiply Matrices
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
74
Perform Scalar Multiplication
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
75
Multiply Matrices
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
76
Multiply Matrices
A) is not defined.
B)
C)
D)
A) is not defined.
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
77
Solve Matrix Equations
Let and
A)
B)
C)
D)
Let and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
78
Solve Matrix Equations
Let and
A)
B)
C)
D)
Let and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
79
Multiply Matrices
A)
B) is not defined.
C)
D)
A)
B) is not defined.
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
80
Perform Scalar Multiplication
Let and . Find 2A - 4B.
A)
B)
C)
D)
Let and . Find 2A - 4B.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck


