Deck 6: Analytic Trigonometry
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/226
Play
Full screen (f)
Deck 6: Analytic Trigonometry
1
Complete the identity.
A)
B) 1
C)
D)
A)
B) 1
C)
D)
A
2
Complete the identity.
A)
B)
C)
D)
A)
B)
C)
D)
A
3
Complete the identity.
A) 1
B) 2
C)
D) 0 )0
A) 1
B) 2
C)
D) 0 )0
A
4
Complete the identity.
A)
B)
C) 1
D)
A)
B)
C) 1
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
5
Complete the identity.
?
A)
B)
C)
D) 2
?
A)
B)
C)
D) 2

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
6
Complete the identity.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
7
Complete the identity.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
8
Complete the identity.
A)
B) 1
C) 0
D)
A)
B) 1
C) 0
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
9
Complete the identity.
?
A) 1
B)
C) 0
D)
?
A) 1
B)
C) 0
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
10
Complete the identity.
A)
B) 0
C)
D)
A)
B) 0
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
11
Complete the identity.
?
A)
B)
C) 1
D) 0
?
A)
B)
C) 1
D) 0

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
12
Complete the identity.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
13
Complete the identity.
?
A)
B)
C)
D)
?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
14
Complete the identity.
?
A) 1
B)
C)
D)
?
A) 1
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
15
Complete the identity.
A) 1
B) 0
D)
A) 1
B) 0
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
16
Complete the identity.
?
A) 2
B) 1
C) 0
D)
?
A) 2
B) 1
C) 0
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
17
Complete the identity.
?
A)
B)
C)
D)
?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
18
Complete the identity.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
19
Complete the identity.
?
A)
B)
C)
D)
?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
20
Complete the identity.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
21
Verify the identity.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
22
Verify the identity.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
23
Verify the identity.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
24
Verify the identity.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
25
Use the graph to complete the identity.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
26
Verify the identity.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
27
Use the graph to complete the identity.
and
A)
B)
C)
D)
and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
28
Complete the identity.
?
A)
B)
C)
D)
?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
29
Verify the identity.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
30
Use the graph to complete the identity.
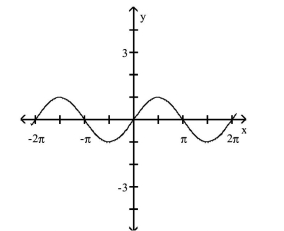
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
31
Show that the equation is not an identity by finding a value of x for which both sides are defined but not equal.
A)
B)
C)
D) 0
A)
B)
C)
D) 0

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
32
Use the Formula for the Cosine of the Difference of Two Angles
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
33
Show that the equation is not an identity by finding a value of x for which both sides are defined but not equal.
A)
B) 0
C)
D)
A)
B) 0
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
34
Use the Formula for the Cosine of the Difference of Two Angles
A)
B)
C)
D) 1 Identify α and β in the following expression which is the right side of the formula for cos (α - β).
A)
B)
C)
D) 1 Identify α and β in the following expression which is the right side of the formula for cos (α - β).

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
35
Use the graph to complete the identity.
?
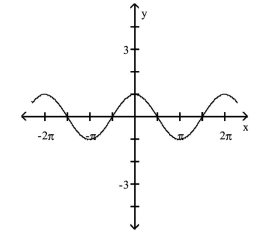
A)
B)
C)
D)
?

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
36
Show that the equation is not an identity by finding a value of x for which both sides are defined but not equal.
A) 0
B)
C)
D)
A) 0
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
37
Verify the identity.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
38
Use the graph to complete the identity.
?
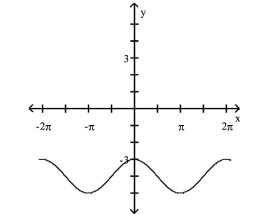
A)
B)
C)
D)
?

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
39
Use the graph to complete the identity.
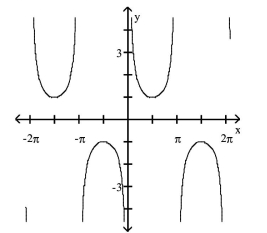
A)
B)
C)
D) Rewrite the expression in terms of the given function or functions.

A)
B)
C)
D) Rewrite the expression in terms of the given function or functions.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
40
Use the graph to complete the identity.
A)
B)
C)
D) 0
A)
B)
C)
D) 0

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
41
Use Sum and Difference Formulas for Cosines and Sines
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
42
Use the given information to find the exact value of the expression.
lies in quadrant II, and lies in quadrant Find .
A)
B)
C)
D)
lies in quadrant II, and lies in quadrant Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
43
Use Sum and Difference Formulas for Cosines and Sines
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
44
Use Sum and Difference Formulas for Cosines and Sines
A)
B)
C)
D) 1
A)
B)
C)
D) 1

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
45
Complete the identity.
?
A)
B)
C)
D)
?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
46
Use the Formula for the Cosine of the Difference of Two Angles
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
47
Complete the identity.
?
A)
B)
C)
D)
?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
48
Complete the identity.
?
A)
B)
C)
D)
?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
49
Use the Formula for the Cosine of the Difference of Two Angles
A)
B)
C)
D) Write the expression as the cosine of an angle, knowing that the expression is the right side of the formula for
A)
B)
C)
D) Write the expression as the cosine of an angle, knowing that the expression is the right side of the formula for

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
50
Use the Formula for the Cosine of the Difference of Two Angles
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
51
Use Sum and Difference Formulas for Cosines and Sines
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
52
Use Sum and Difference Formulas for Cosines and Sines
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
53
Complete the identity.
?
A)
B)
C)
D)
?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
54
Use Sum and Difference Formulas for Cosines and Sines
A)
B)
C)
D) Find the exact value of the expression.
A)
B)
C)
D) Find the exact value of the expression.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
55
Use Sum and Difference Formulas for Cosines and Sines
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
56
Use the Formula for the Cosine of the Difference of Two Angles
A)
B)
C)
D) Find the exact value of the expression.
A)
B)
C)
D) Find the exact value of the expression.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
57
Complete the identity.
?
A)
B)
C)
D)
?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
58
Use the Formula for the Cosine of the Difference of Two Angles
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
59
Use Sum and Difference Formulas for Cosines and Sines
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
60
Use Sum and Difference Formulas for Cosines and Sines
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
61
Verify the identity.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
62
Use the given information to find the exact value of the expression.
lies in quadrant IV, and lies in quadrant III Find .
A)
B)
C)
D)
lies in quadrant IV, and lies in quadrant III Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
63
Verify the identity.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
64
Verify the identity.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
65
Use Sum and Difference Formulas for Tangents
Find the exact value by using a difference identity.
A)
B)
C)
D)
Find the exact value by using a difference identity.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
66
Use Sum and Difference Formulas for Tangents
Find the exact value by using a difference identity.
A)
B)
C)
D)
Find the exact value by using a difference identity.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
67
Describe the graph using another equation.
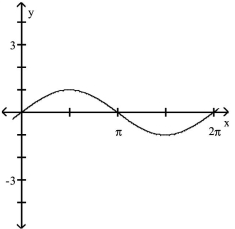
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
68
Use the given information to find the exact value of the expression.
lies in quadrant III, and lies in quadrant II Find .
A)
B)
C)
D)
lies in quadrant III, and lies in quadrant II Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
69
Complete the identity.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
70
Complete the identity.
?
A)
B)
C)
D)
?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
71
Verify the identity.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
72
Use the given information to find the exact value of the expression.
lies in quadrant III, and lies in quadrant II Find
A)
B)
C)
D)
lies in quadrant III, and lies in quadrant II Find
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
73
Use the given information to find the exact value of the expression.
lies in quadrant II, and lies in quadrant I Find .
A)
B)
C)
D)
lies in quadrant II, and lies in quadrant I Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
74
Complete the identity.
?
A)
B)
C)
D)
?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
75
Describe the graph using another equation.
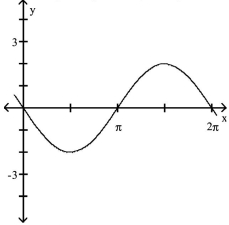
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
76
Use the given information to find the exact value of the expression.
lies in quadrant II, and lies in quadrant I Find .
A)
B)
C)
D)
lies in quadrant II, and lies in quadrant I Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
77
Verify the identity.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
78
Verify the identity.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
79
Use the given information to find the exact value of the expression.
lies in quadrant , and lies in quadrant I Find
A)
B)
C)
D)
lies in quadrant , and lies in quadrant I Find
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck
80
Verify the identity.

Unlock Deck
Unlock for access to all 226 flashcards in this deck.
Unlock Deck
k this deck


