Exam 6: Analytic Trigonometry
Exam 1: Equations and Inequalities425 Questions
Exam 2: Functions and Graphs359 Questions
Exam 3: Polynomial and Rational Functions532 Questions
Exam 4: Exponential and Logarithmic Functions270 Questions
Exam 5: Trigonometric Functions386 Questions
Exam 6: Analytic Trigonometry226 Questions
Exam 7: Additional Topics in Trigonometry264 Questions
Exam 8: Systems of Equations and Inequalities288 Questions
Exam 9: Matrices and Determinants152 Questions
Exam 10: Conic Sections and Analytic Geometry228 Questions
Exam 11: Sequences, Induction, and Probability304 Questions
Exam 12: Prerequisites: Fundamental Concepts of Algebra409 Questions
Select questions type
Use substitution to determine whether the given x-value is a solution of the equation.
Find All Solutions of a Trigonometric Equation
-
Free
(Multiple Choice)
4.9/5  (39)
(39)
Correct Answer:
A
Use the given information to find the exact value of the trigonometric function.
- Find .
Free
(Multiple Choice)
4.9/5  (41)
(41)
Correct Answer:
A
Solve the equation on the interval [0, 2π).
-
Free
(Multiple Choice)
4.8/5  (37)
(37)
Correct Answer:
A
Use substitution to determine whether the given x-value is a solution of the equation.
Find All Solutions of a Trigonometric Equation
-
(Multiple Choice)
4.7/5  (39)
(39)
Use the figure to find the exact value of the trigonometric function.
-Find .
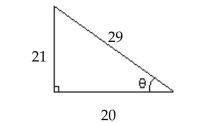
(Multiple Choice)
4.9/5  (31)
(31)
Use the Formula for the Cosine of the Difference of Two Angles
-
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-If a projectile is fired at an angle and initial velocity , then the horizontal distance traveled by the projectile is given by . Express as a function of .
(Multiple Choice)
4.8/5  (34)
(34)
Use the given information to find the exact value of the expression.
- lies in quadrant II, and lies in quadrant I Find .
(Multiple Choice)
4.9/5  (40)
(40)
Use the given information to find the exact value of the trigonometric function.
- lies in quadrant I Find
(Multiple Choice)
4.9/5  (30)
(30)
Use the Formula for the Cosine of the Difference of Two Angles
-
(Multiple Choice)
4.8/5  (37)
(37)
Show that the equation is not an identity by finding a value of x for which both sides are defined but not equal.
-
(Multiple Choice)
4.7/5  (31)
(31)
Showing 1 - 20 of 226
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)