Deck 15: Graph Theory
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/110
Play
Full screen (f)
Deck 15: Graph Theory
1
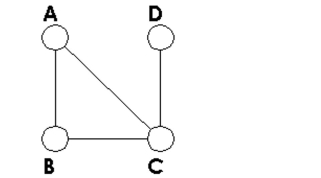
Determine whether the graph is connected or disconnected.
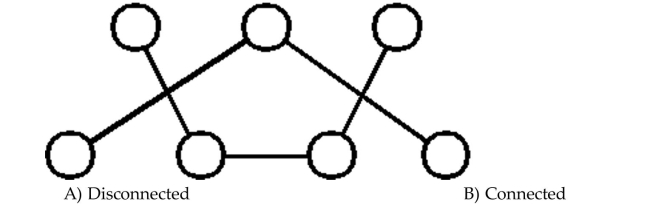

A
2
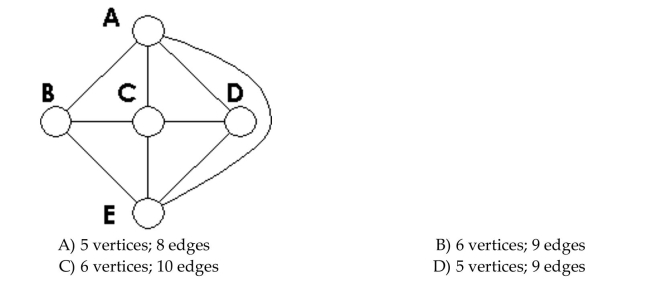
D
3
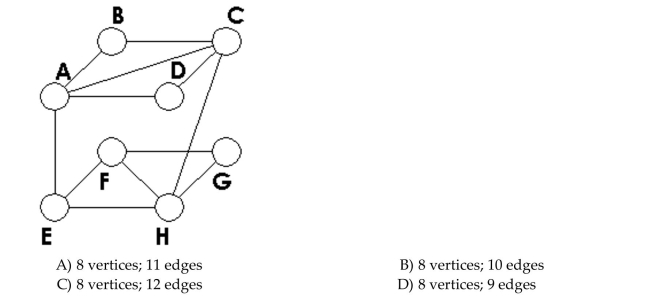
C
4
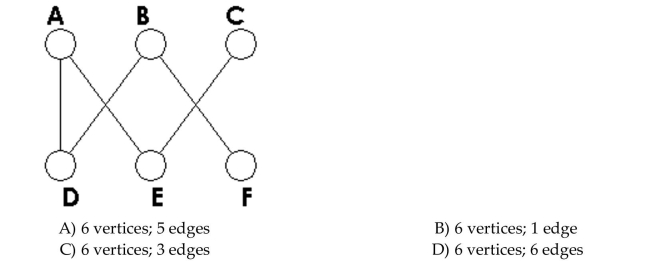

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
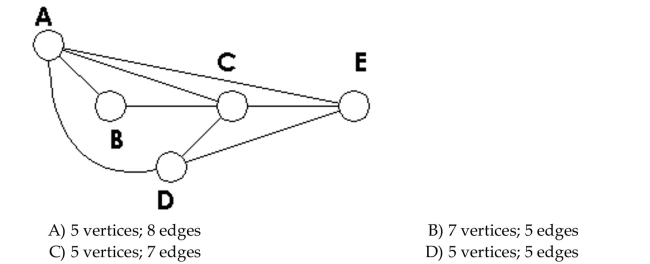
5
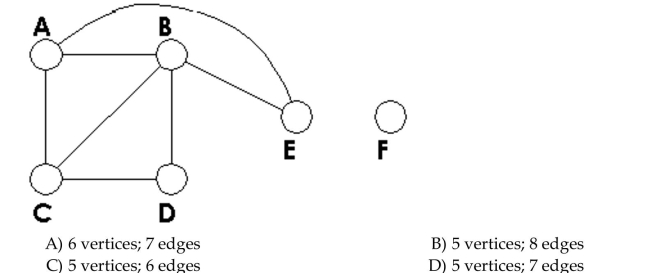
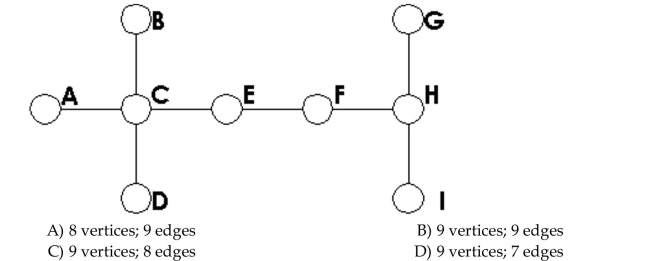
A)4 vertices; 4 edges
B)4 vertices; 3 edges
C)5 vertices; 4 edges
D)4 vertices; 5 edges

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
6
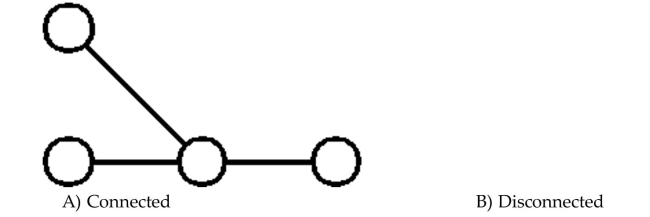
Determine whether the graph is connected or disconnected.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
7

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
8
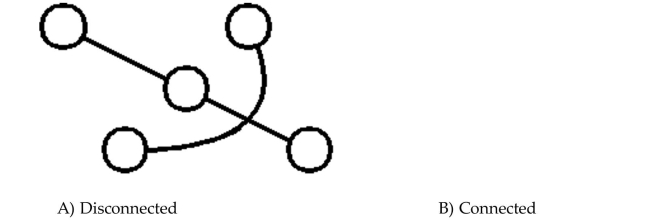
Determine whether the graph is connected or disconnected.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
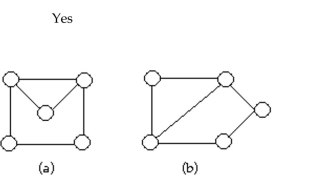
9
Determine whether the two graphs are isomorphic. If they are, illustrate the isomorphism.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
10

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
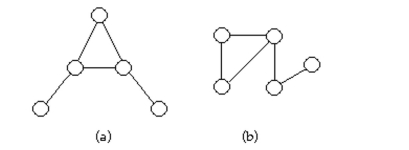
11
Determine whether the two graphs are isomorphic. If they are, illustrate the isomorphism.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
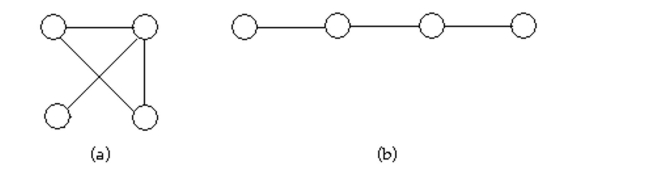
12
Determine whether the two graphs are isomorphic. If they are, illustrate the isomorphism.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
13
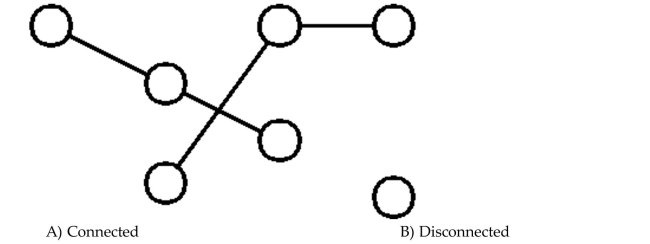
Determine whether the graph is connected or disconnected.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
14

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
15
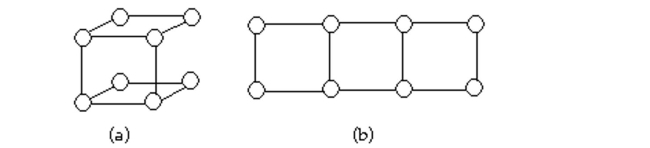
Determine whether the two graphs are isomorphic. If they are, illustrate the isomorphism.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
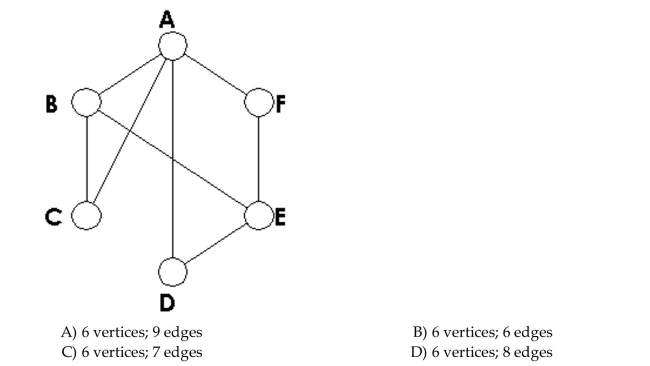
16

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
17
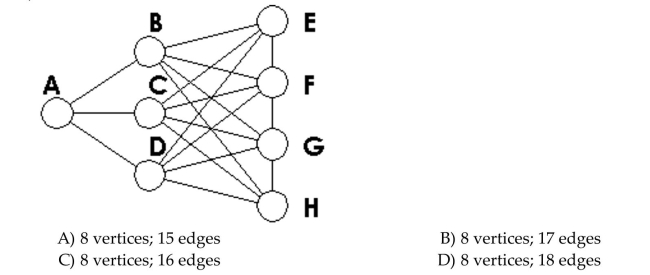

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
18
Determine whether the two graphs are isomorphic. If they are, illustrate the isomorphism.
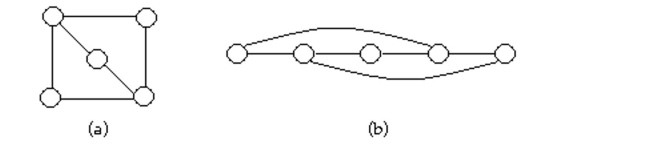


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
19
Determine whether the two graphs are isomorphic. If they are, illustrate the isomorphism.
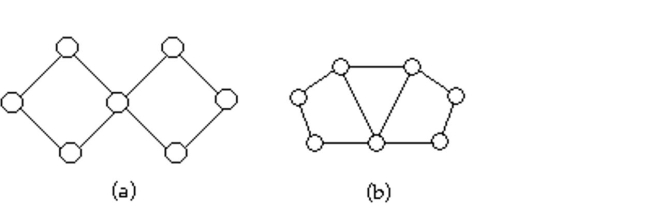


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
20
Determine whether the two graphs are isomorphic. If they are, illustrate the isomorphism.
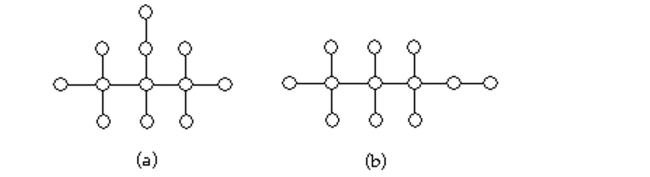


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
21
Determine whether the graph is connected or disconnected.
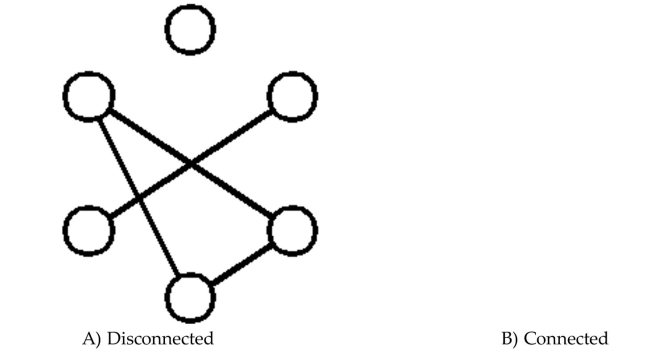


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
22
Determine how many components the graph has.
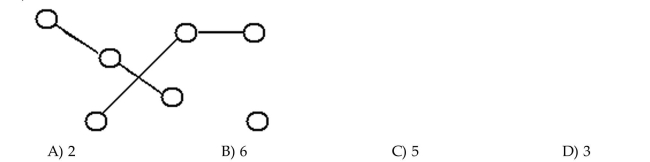


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
23
Use the theorem that relates the sum of degrees to the number of edges to determine the number of edges in the graph.
A graph with 5 vertices, one of degree 4, three of degree 3, and one of degree 1.
A)4 edges
B)7 edges
C)3 edges
D)8 edges
A graph with 5 vertices, one of degree 4, three of degree 3, and one of degree 1.
A)4 edges
B)7 edges
C)3 edges
D)8 edges

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
24
Determine whether the graph is connected or disconnected.
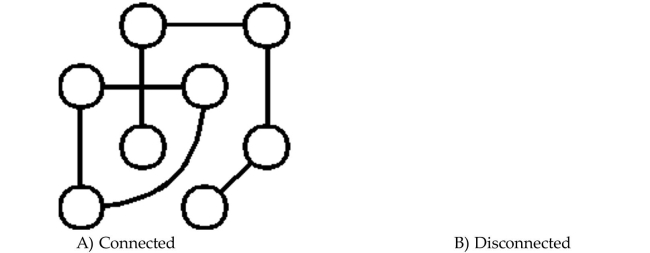


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
25
Use the theorem that relates the sum of degrees to the number of edges to determine the number of edges in the graph.
A graph with 6 vertices, two of degree 2, three of degree 1, and one of degree 3.
A)20 edges
B)10 edges
C)5 edges
D)6 edges
A graph with 6 vertices, two of degree 2, three of degree 1, and one of degree 3.
A)20 edges
B)10 edges
C)5 edges
D)6 edges

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
26
Determine how many components the graph has.
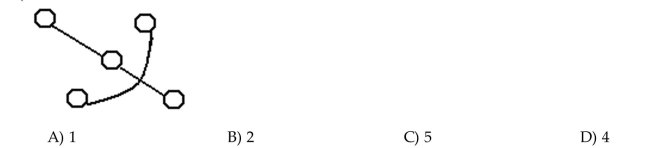
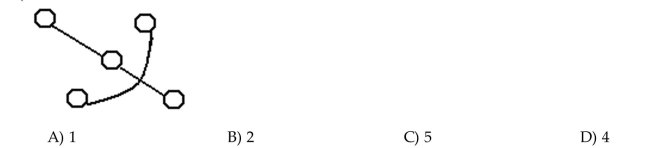

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
27
Use the theorem that relates the sum of degrees to the number of edges to determine the number of edges in the graph.
A graph with 5 vertices, three of degree 2 and two of degree 3.
A)12 edges
B)6 edges
C)9 edges
D)5 edges
A graph with 5 vertices, three of degree 2 and two of degree 3.
A)12 edges
B)6 edges
C)9 edges
D)5 edges

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
28
Determine how many components the graph has.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
29
Determine how many components the graph has.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
30
Determine how many components the graph has.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
31
Determine how many components the graph has.
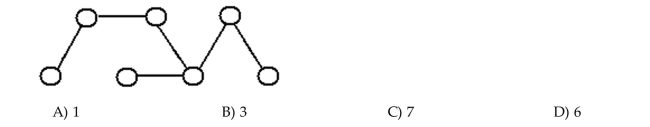
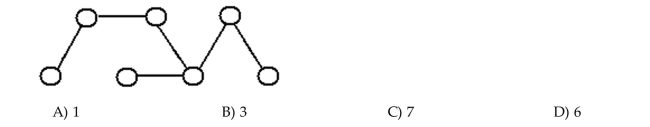

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
32
Determine how many components the graph has.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
33
Use the theorem that relates the sum of degrees to the number of edges to determine the number of edges in the graph.
A graph with 4 vertices each of degree 2.
A)6 edges
B)16 edges
C)8 edges
D)4 edges
A graph with 4 vertices each of degree 2.
A)6 edges
B)16 edges
C)8 edges
D)4 edges

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
34
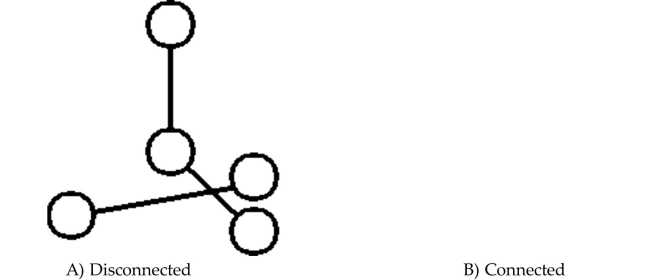
Determine whether the graph is connected or disconnected.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
35
Determine how many components the graph has.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
36
Determine how many components the graph has.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
37
Determine how many components the graph has.
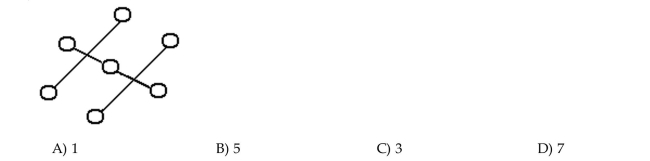
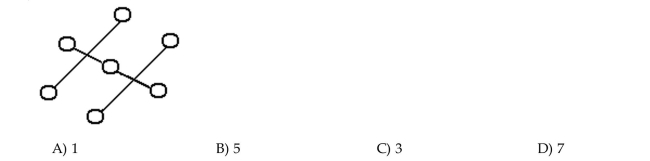

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
38
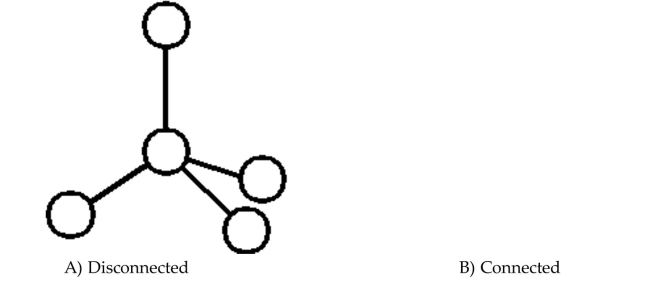
Determine whether the graph is connected or disconnected.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
39
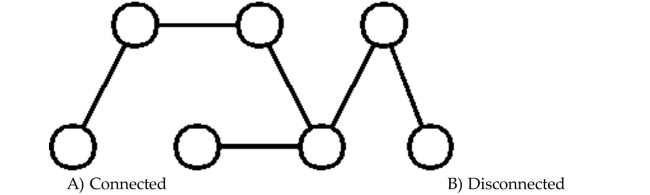
Determine whether the graph is connected or disconnected.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
40
Determine whether the graph is connected or disconnected.
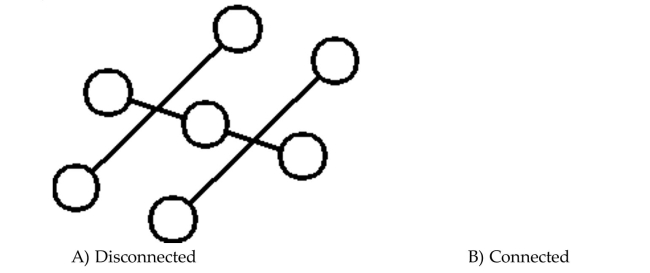


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
41
Use the theorem that relates the sum of degrees to the number of edges to determine the number of edges in the graph.
A graph with 6 vertices, one of degree 5, three of degree 1, and two of degree 2.
A)8 edges
B)4 edges
C)6 edges
D)12 edges
A graph with 6 vertices, one of degree 5, three of degree 1, and two of degree 2.
A)8 edges
B)4 edges
C)6 edges
D)12 edges

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
42
Determine whether the sequence of vertices is i)a walk, ii)a path, iii)a circuit in the given graph.
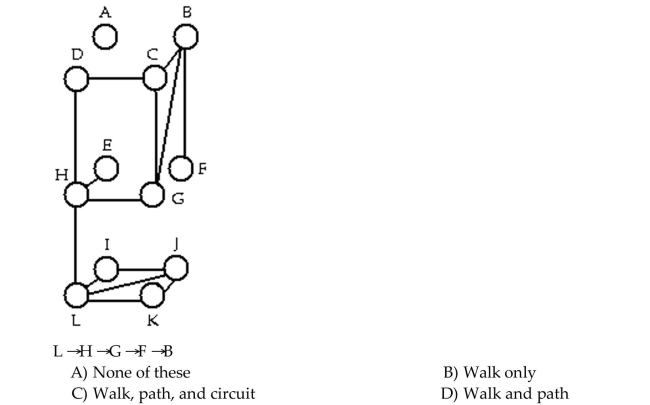


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
43
Determine whether the graph is a complete graph.
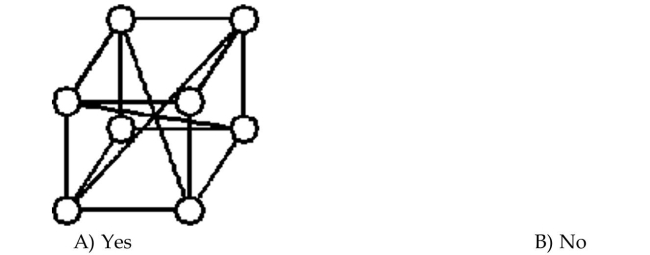


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
44
Determine whether the graph is a complete graph.
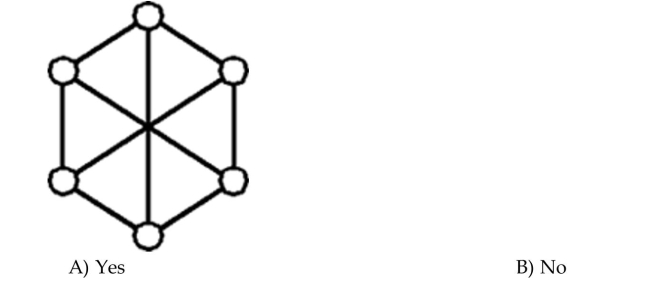


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
45
Determine whether the sequence of vertices is i)a walk, ii)a path, iii)a circuit in the given graph.
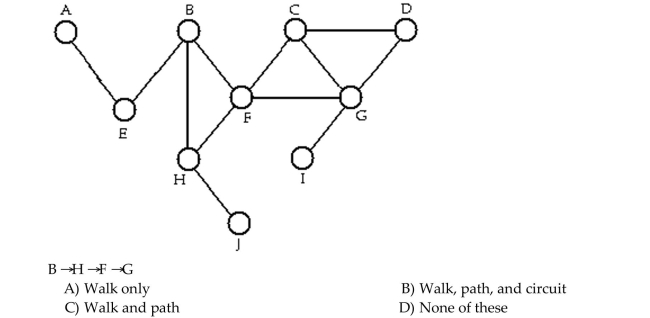


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
46
Use the theorem that relates the sum of degrees to the number of edges to determine the number of edges in the graph.
A graph with 7 vertices, one of degree 6 and six of degree 1.
A)6 edges
B)7 edges
C)14 edges
D)13 edges
A graph with 7 vertices, one of degree 6 and six of degree 1.
A)6 edges
B)7 edges
C)14 edges
D)13 edges

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
47
Determine whether the graph is a complete graph.
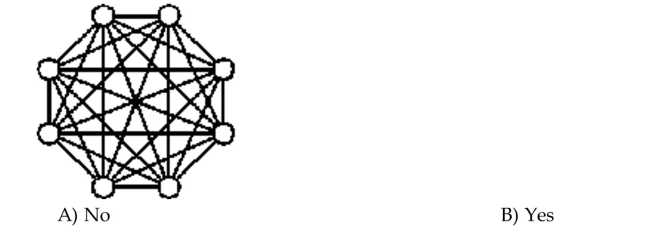
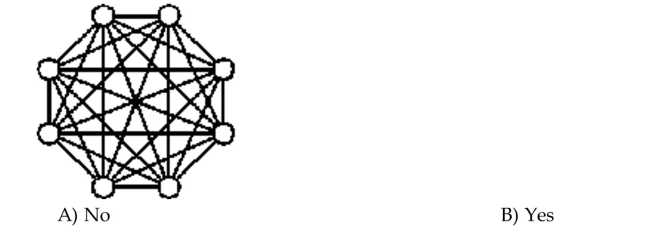

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
48
Determine whether the sequence of vertices is i)a walk, ii)a path, iii)a circuit in the given graph.
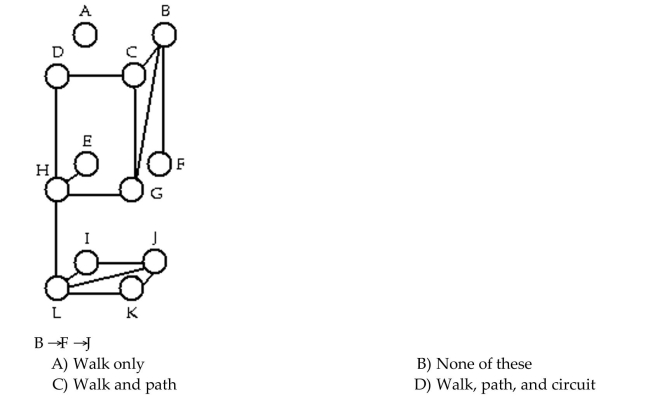


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
49
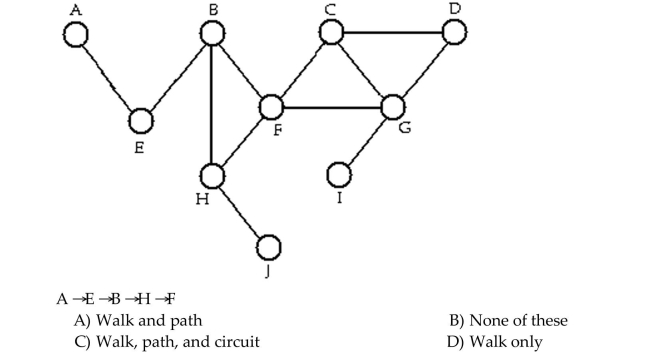
Determine whether the sequence of vertices is i)a walk, ii)a path, iii)a circuit in the given graph.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
50
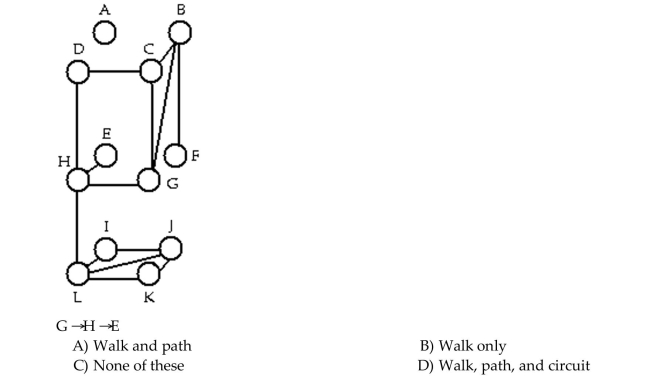
Determine whether the sequence of vertices is i)a walk, ii)a path, iii)a circuit in the given graph.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
51
Determine whether the graph is a complete graph.
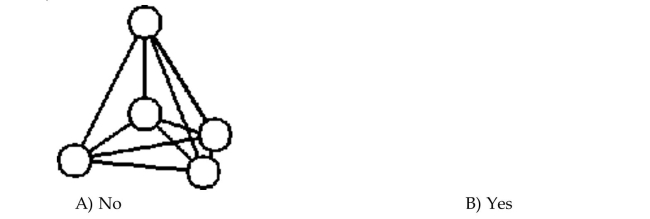
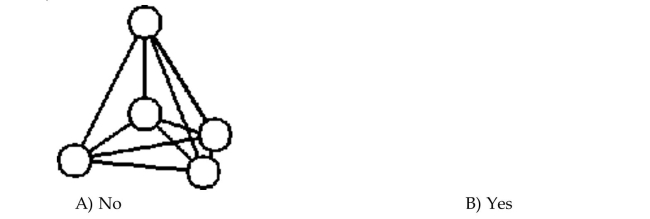

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
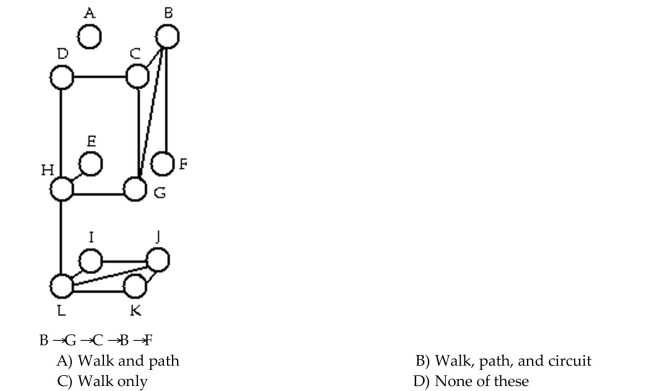
52
Determine whether the sequence of vertices is i)a walk, ii)a path, iii)a circuit in the given graph.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
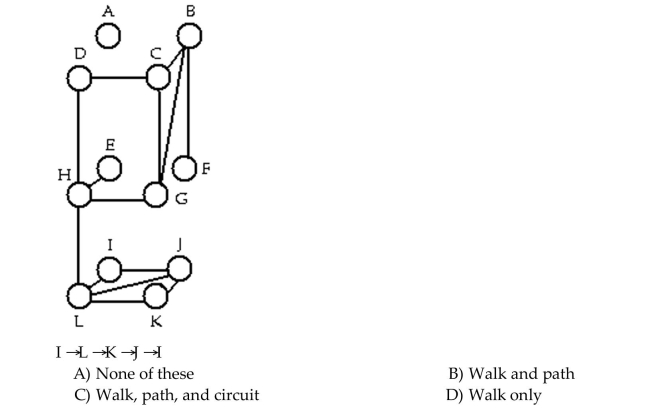
53
Determine whether the sequence of vertices is i)a walk, ii)a path, iii)a circuit in the given graph.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
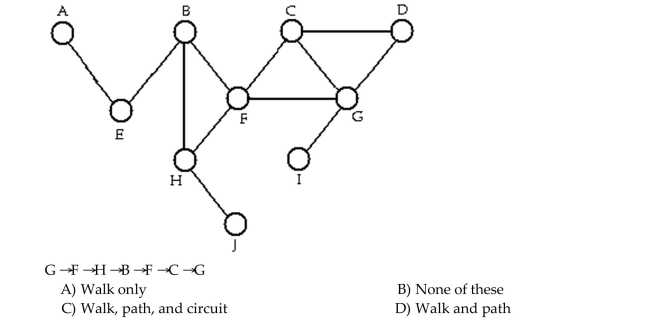
54
Determine whether the sequence of vertices is i)a walk, ii)a path, iii)a circuit in the given graph.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
55
Use the theorem that relates the sum of degrees to the number of edges to determine the number of edges in the graph.
A graph with 8 vertices, two of degree 2, four of degree 3, and two of degree 1.
A)9 edges
B)6 edges
C)3 edges
D)18 edges
A graph with 8 vertices, two of degree 2, four of degree 3, and two of degree 1.
A)9 edges
B)6 edges
C)3 edges
D)18 edges

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
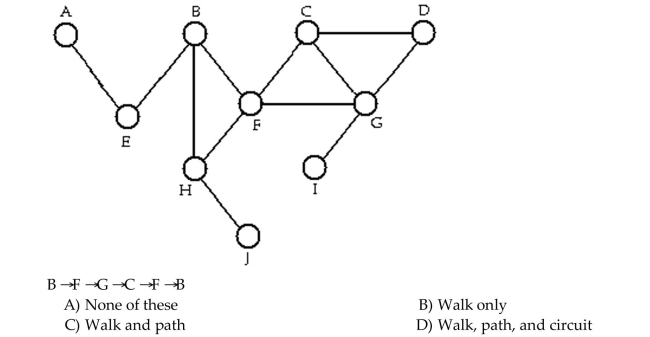
56
Determine whether the sequence of vertices is i)a walk, ii)a path, iii)a circuit in the given graph.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
57
Use the theorem that relates the sum of degrees to the number of edges to determine the number of edges in the graph.
A graph with 7 vertices, one of degree 4, three of degree 3, and three of degree 1.
A)4 edges
B)8 edges
C)16 edges
D)12 edges
A graph with 7 vertices, one of degree 4, three of degree 3, and three of degree 1.
A)4 edges
B)8 edges
C)16 edges
D)12 edges

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
58
Use the theorem that relates the sum of degrees to the number of edges to determine the number of edges in the graph.
A graph with 10 vertices, three of degree 5, three of degree 3, two of degree 2, and two of degree 1.
A)18 edges
B)12 edges
C)11 edges
D)15 edges
A graph with 10 vertices, three of degree 5, three of degree 3, two of degree 2, and two of degree 1.
A)18 edges
B)12 edges
C)11 edges
D)15 edges

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
59
Use the theorem that relates the sum of degrees to the number of edges to determine the number of edges in the graph.
A graph with 8 vertices, one of degree 4, three of degree 2, and four of degree 1.
A)6 edges
B)7 edges
C)14 edges
D)5 edges
A graph with 8 vertices, one of degree 4, three of degree 2, and four of degree 1.
A)6 edges
B)7 edges
C)14 edges
D)5 edges

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
60
Determine whether the sequence of vertices is i)a walk, ii)a path, iii)a circuit in the given graph.
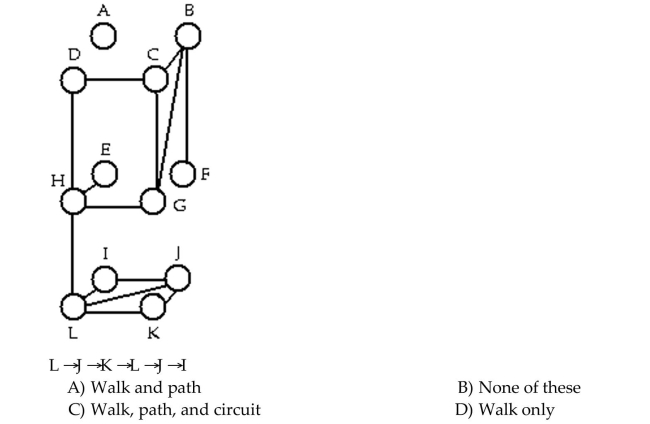


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
61
Determine whether the graph is a complete graph.
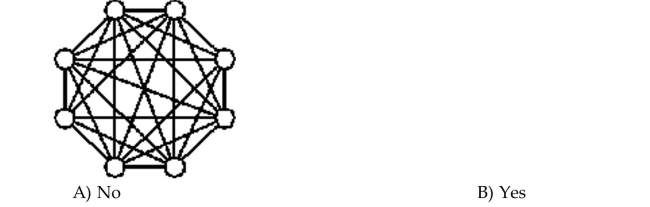
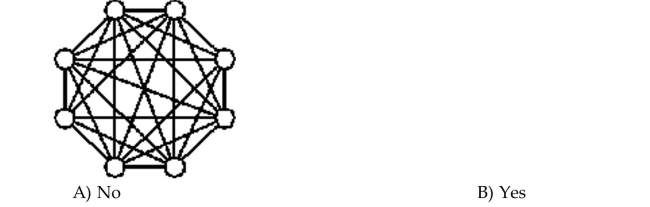

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
62
Represent the following with a graph.
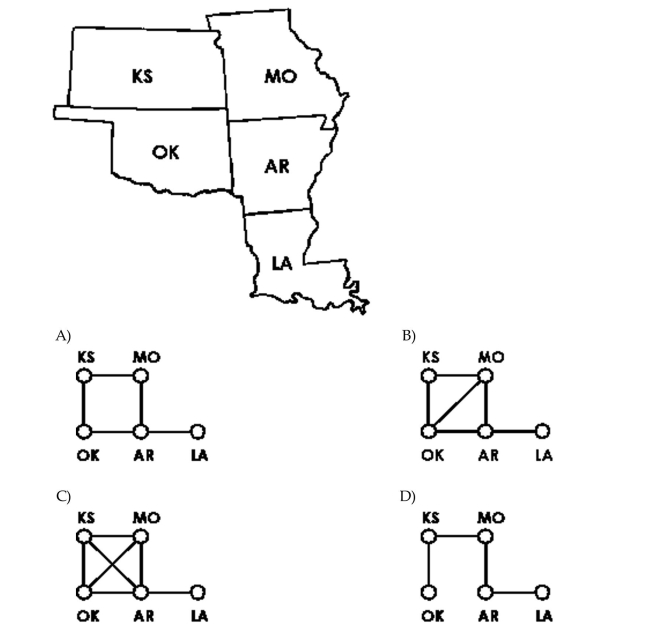


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
63
Represent the following with a graph.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
64
Determine whether the graph is a complete graph.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the problem.
Six freshmen move into a dormitory suite at the beginning of the semester. In order to get
to know one another, they decide to have breakfast in pairs for the next few days, each
student having a different breakfast partner each day until each student has had breakfast
with all other students exactly once. Draw a graph with vertices representing students and
edges representing breakfast dates. How many breakfasts will occur? How many days will
the process take?
Six freshmen move into a dormitory suite at the beginning of the semester. In order to get
to know one another, they decide to have breakfast in pairs for the next few days, each
student having a different breakfast partner each day until each student has had breakfast
with all other students exactly once. Draw a graph with vertices representing students and
edges representing breakfast dates. How many breakfasts will occur? How many days will
the process take?

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
66
There are 9 members on a baseball team. At the end of the game, each member of the team shakes hands with each member of the opposing team. How many handshakes occur?
A)40.5
B)162
C)81
D)9
A)40.5
B)162
C)81
D)9

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
67
Determine whether the graph is a complete graph.
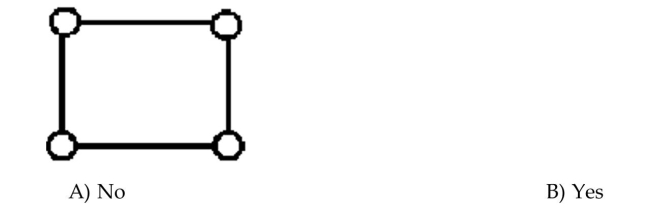


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
68
Determine whether the graph is a complete graph.
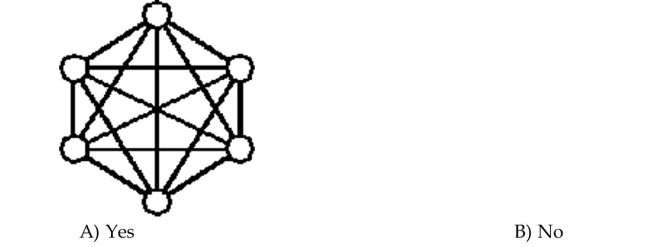


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
69
Determine whether the graph is a complete graph.
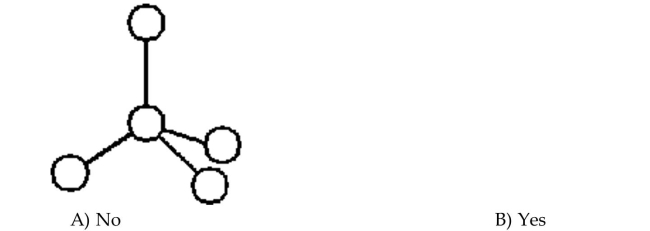
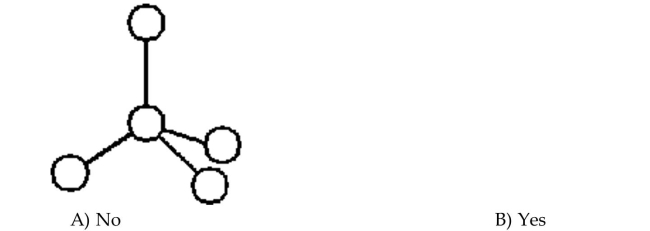

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the problem.
A computer network is to be built by connecting two "server" computers to 6 "client"
computers. Each client computer is connected to each server by a single cable. Also, the
two servers are connected by a single cable. Draw a graph with vertices representing
computers and edges representing cables. How many cables are required? Is the graph of
the network a complete graph?
A computer network is to be built by connecting two "server" computers to 6 "client"
computers. Each client computer is connected to each server by a single cable. Also, the
two servers are connected by a single cable. Draw a graph with vertices representing
computers and edges representing cables. How many cables are required? Is the graph of
the network a complete graph?

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
71
Solve the problem.
Two schools play a tennis tournament. Each school has a team made up of 5 players, and
each player must play one match with each player of the opposing team. Draw a graph
with vertices representing players and edges representing matches. How many matches
will be played in the tournament?
Two schools play a tennis tournament. Each school has a team made up of 5 players, and
each player must play one match with each player of the opposing team. Draw a graph
with vertices representing players and edges representing matches. How many matches
will be played in the tournament?

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
72
Represent the following with a graph.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
73
Determine whether the graph is a complete graph.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
74
James, Carl, Mark, Antonio, Phillip, and Brad are friends at college. Carl, Antonio and
Phillip have calculus together. Brad, Carl, and Mark have the same English composition
class. Draw a graph with vertices representing students and edges representing the relation
"take a common class". How many components does the graph have? Identify a subgraph
that is a complete subgraph with three vertices.
Phillip have calculus together. Brad, Carl, and Mark have the same English composition
class. Draw a graph with vertices representing students and edges representing the relation
"take a common class". How many components does the graph have? Identify a subgraph
that is a complete subgraph with three vertices.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
75
James, Carl, Mark, Antonio, Phillip, and Brad are friends at college. James, Antonio and
Phillip have calculus together. Brad and Carl have the same English composition class.
Draw a graph with vertices representing students and edges representing the relation "take
a common class". How many components does the graph have? Identify a subgraph that is
a complete subgraph with three vertices.
Phillip have calculus together. Brad and Carl have the same English composition class.
Draw a graph with vertices representing students and edges representing the relation "take
a common class". How many components does the graph have? Identify a subgraph that is
a complete subgraph with three vertices.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
76
Represent the following with a graph.
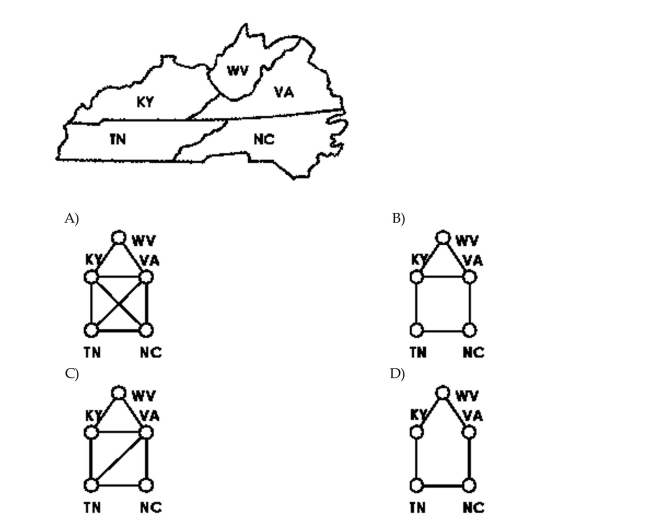
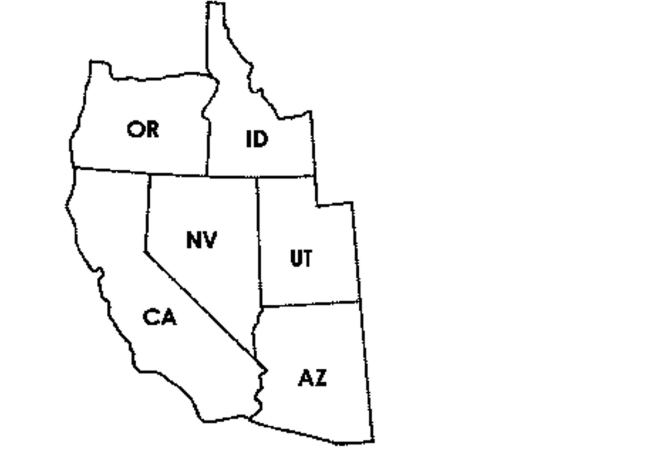
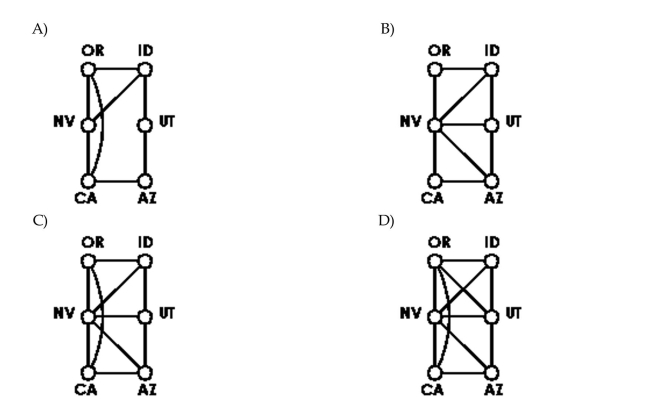
Create a graph that models the bordering relationship among the states shown in the map. Use vertices to represent the states and edges to represent common borders.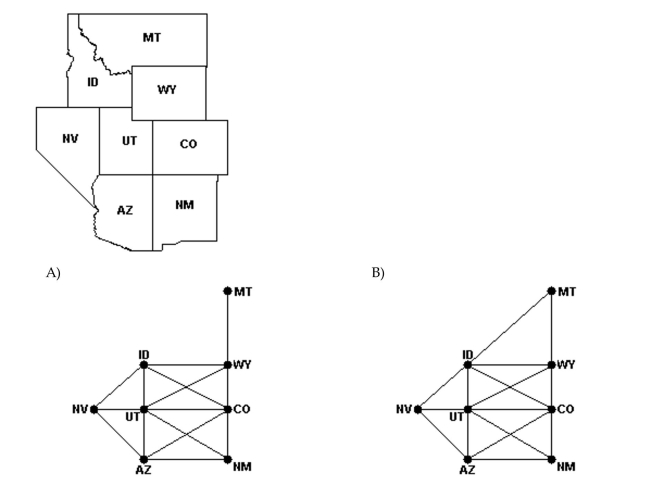
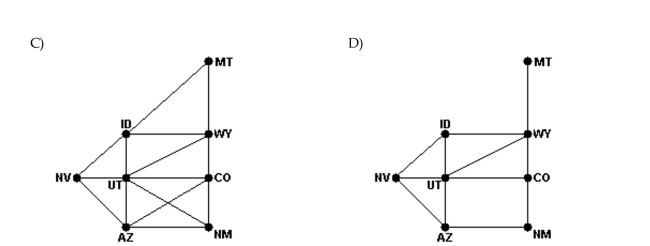
Create a graph that models the bordering relationship among the states shown in the map. Use vertices to represent the states and edges to represent common borders.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
77
Seven family members are planning a picnic. They work out the details with a few phone calls. One family member has 5 conversations, two have 3 conversations, and one has only 1 conversation.
How many phone conversations are there?
A)9
B)12
C)6
D)18
How many phone conversations are there?
A)9
B)12
C)6
D)18

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
78
Solve the problem.
A psychology class decides to compare the social attitudes of students from urban and
rural backgrounds. Class members are divided into two groups: 5 students who grew up in
an urban setting and 3 students who grew up in a rural environment. Each member of a
group is to meet with each member of the other group one time, at which time the pair will
interview each other by asking questions about current social issues. After all the
interviews are completed, the students will compile the results and draw conclusions.
Draw a graph with vertices representing students and edges representing interviews. How
many interviews will there be?
A psychology class decides to compare the social attitudes of students from urban and
rural backgrounds. Class members are divided into two groups: 5 students who grew up in
an urban setting and 3 students who grew up in a rural environment. Each member of a
group is to meet with each member of the other group one time, at which time the pair will
interview each other by asking questions about current social issues. After all the
interviews are completed, the students will compile the results and draw conclusions.
Draw a graph with vertices representing students and edges representing interviews. How
many interviews will there be?

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
79
Solve the problem.
An internet user is participating simultaneously in one-on-one chat sessions with 5 other
people. Draw a graph with vertices representing users and edges representing chat
sessions. How many chat sessions are occurring?
An internet user is participating simultaneously in one-on-one chat sessions with 5 other
people. Draw a graph with vertices representing users and edges representing chat
sessions. How many chat sessions are occurring?

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
80
Ten police officers patrol in pairs. Two officers have each patrolled with 5 other officers, four officers have patrolled with 3 others, two have patrolled with 2 others, and two have patrolled with
Only 1 other officer. How many different patrol pairs have there been?
A)11
B)14
C)28
D)7
Only 1 other officer. How many different patrol pairs have there been?
A)11
B)14
C)28
D)7

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck


