Exam 15: Graph Theory
Exam 1: The Art of Problem Solving190 Questions
Exam 2: The Basic Concepts of Set Theory316 Questions
Exam 3: Introduction to Logic315 Questions
Exam 4: Numeration Systems245 Questions
Exam 5: Number Theory171 Questions
Exam 6: The Real Numbers and Their Representations401 Questions
Exam 7: The Basic Concepts of Algebra273 Questions
Exam 8: Graphs, Functions, and Systems of Equations and Inequalities136 Questions
Exam 9: Geometry182 Questions
Exam 10: Counting Methods213 Questions
Exam 11: Probability140 Questions
Exam 12: Statistics152 Questions
Exam 13: Personal Financial Management260 Questions
Exam 14: Trigonometry Formerly234 Questions
Exam 15: Graph Theory110 Questions
Exam 16: Voting and Apportionment99 Questions
Select questions type
Solve the problem.
-A computer network is to be built by connecting two "server" computers to 6 "client"
computers. Each client computer is connected to each server by a single cable. Also, the
two servers are connected by a single cable. Draw a graph with vertices representing
computers and edges representing cables. How many cables are required? Is the graph of
the network a complete graph?
Free
(Essay)
4.7/5  (42)
(42)
Correct Answer:
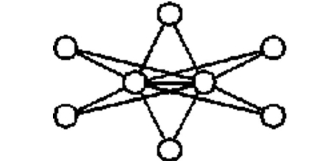
Thirteen cables are required.
The graph is not complete: the clients are not directly connected.
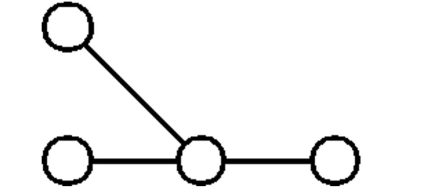
Determine whether the graph is connected or disconnected.
-
Free
(Multiple Choice)
4.8/5  (39)
(39)
Correct Answer:
A
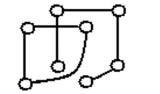
Determine how many components the graph has.
-
Free
(Multiple Choice)
4.8/5  (30)
(30)
Correct Answer:
B
Solve the problem.
-A psychology class decides to compare the social attitudes of students from urban and
rural backgrounds. Class members are divided into two groups: 5 students who grew up in
an urban setting and 3 students who grew up in a rural environment. Each member of a
group is to meet with each member of the other group one time, at which time the pair will
interview each other by asking questions about current social issues. After all the
interviews are completed, the students will compile the results and draw conclusions.
Draw a graph with vertices representing students and edges representing interviews. How
many interviews will there be?
(Essay)
4.8/5  (28)
(28)
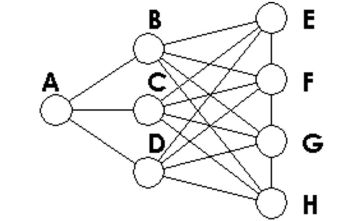
Determine how many vertices and how many edges the graph has.
-
(Multiple Choice)
4.9/5  (36)
(36)
Use the theorem that relates the sum of degrees to the number of edges to determine the number of edges in the graph.
-A graph with 5 vertices, one of degree 4, three of degree 3, and one of degree 1.
(Multiple Choice)
4.8/5  (33)
(33)
Determine whether the two graphs are isomorphic. If they are, illustrate the isomorphism.
-Yes
(a)
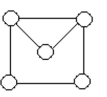 (b)
(b)
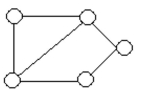
(Essay)
4.8/5  (39)
(39)
Determine whether the two graphs are isomorphic. If they are, illustrate the isomorphism.
-(a)
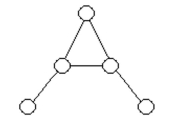 (b)
(b)
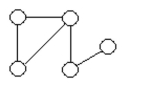
(Essay)
4.9/5  (32)
(32)
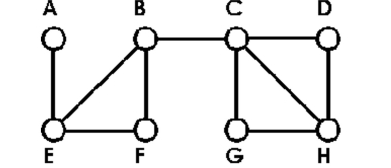
Identify the cut edges in the graph or say there are none.
-
(Multiple Choice)
4.9/5  (41)
(41)
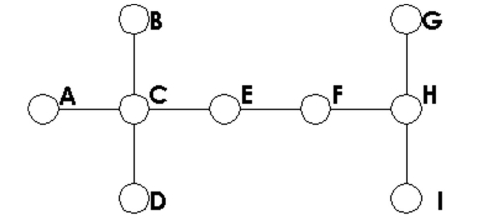
Determine how many vertices and how many edges the graph has.
-
(Multiple Choice)
4.8/5  (40)
(40)
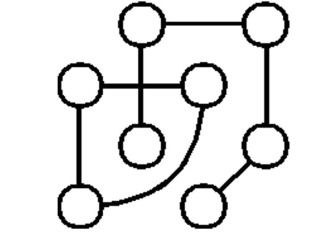
Determine whether the graph is connected or disconnected.
-
(Multiple Choice)
4.8/5  (45)
(45)
Solve the problem.
-Six freshmen move into a dormitory suite at the beginning of the semester. In order to get
to know one another, they decide to have breakfast in pairs for the next few days, each
student having a different breakfast partner each day until each student has had breakfast
with all other students exactly once. Draw a graph with vertices representing students and
edges representing breakfast dates. How many breakfasts will occur? How many days will
the process take?
(Essay)
4.8/5  (31)
(31)
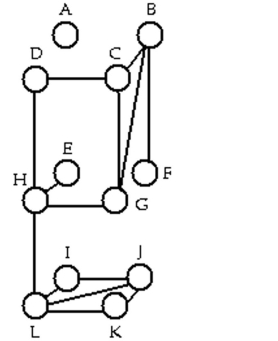
Determine whether the sequence of vertices is i)a walk, ii)a path, iii)a circuit in the given graph.
-
(Multiple Choice)
4.8/5  (33)
(33)
There are 9 members on a baseball team. At the end of the game, each member of the team shakes hands with each member of the opposing team. How many handshakes occur?
(Multiple Choice)
4.9/5  (33)
(33)
Showing 1 - 20 of 110
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)