Deck 4: Probability Concepts
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/133
Play
Full screen (f)
Deck 4: Probability Concepts
1
Write the word or phrase that best completes each statement or answers the question.
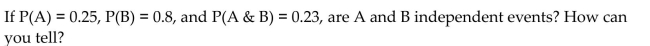
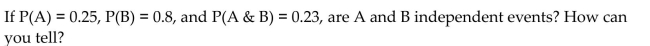
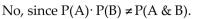
2
Provide an appropriate response.
Consider the following counting problem. Eight women and seven men are waiting in line at a movie theater. How many ways are there to arrange these 15 people amongst themselves such that
The eight women occupy the first eight places and the seven men the last seven places?
To solve this problem, which of the following rules would you use?
A)Both the combinations rule and the basic counting rule
B)The basic counting rule only
C)The permutations rule only
D)Both the permutations rule and the basic counting rule
Consider the following counting problem. Eight women and seven men are waiting in line at a movie theater. How many ways are there to arrange these 15 people amongst themselves such that
The eight women occupy the first eight places and the seven men the last seven places?
To solve this problem, which of the following rules would you use?
A)Both the combinations rule and the basic counting rule
B)The basic counting rule only
C)The permutations rule only
D)Both the permutations rule and the basic counting rule
D
3
Write the word or phrase that best completes each statement or answers the question.
Construct a Venn diagram portraying four events A, B, C, and D such that the collection of
events A, B, and C is mutually exclusive, the collection of events A, B, and D is mutually
exclusive, but the collection of events A, B, C, and D is not mutually exclusive.
Construct a Venn diagram portraying four events A, B, C, and D such that the collection of
events A, B, and C is mutually exclusive, the collection of events A, B, and D is mutually
exclusive, but the collection of events A, B, C, and D is not mutually exclusive.
Answers will vary.
4
Write the word or phrase that best completes each statement or answers the question.
Explain why an event and its complement are always mutually exclusive and exhaustive.
Explain why an event and its complement are always mutually exclusive and exhaustive.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
5
Provide an appropriate response.
Suppose that S and T are mutually exclusive events. Which of the following statements is true?
A)S and T must also be independent.
B)S and T cannot possibly be independent.
C)S and T may or may not be independent.
Suppose that S and T are mutually exclusive events. Which of the following statements is true?
A)S and T must also be independent.
B)S and T cannot possibly be independent.
C)S and T may or may not be independent.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
6
Write the word or phrase that best completes each statement or answers the question.
Discuss the range of possible values for probabilities. Give examples to support each.
Discuss the range of possible values for probabilities. Give examples to support each.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
7
Write the word or phrase that best completes each statement or answers the question.
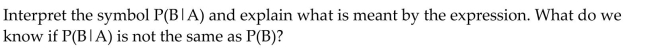
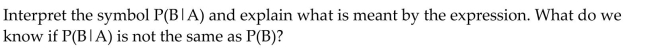

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
8
Provide an appropriate response.
Consider the following counting problem. Allison is trying to decide which three of her eight new books to take on vacation with her. How many different ways can she choose the three books?
To solve this problem which of the following rules would you use?
A)The combinations rule only
B)The basic counting rule only
C)Both the permutations rule and the basic counting rule
D)The permutations rule only
Consider the following counting problem. Allison is trying to decide which three of her eight new books to take on vacation with her. How many different ways can she choose the three books?
To solve this problem which of the following rules would you use?
A)The combinations rule only
B)The basic counting rule only
C)Both the permutations rule and the basic counting rule
D)The permutations rule only

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
9
Provide an appropriate response.
Consider the following counting problem. A pool of possible jurors consists of 11 men and 13 women. How many different juries consisting of 5 women and 7 men are possible?
To solve this problem, which of the following rules would you use?
A)Both the combinations rule and the basic counting rule
B)The combinations rule only
C)Both the permutations rule and the basic counting rule
D)The basic counting rule only
Consider the following counting problem. A pool of possible jurors consists of 11 men and 13 women. How many different juries consisting of 5 women and 7 men are possible?
To solve this problem, which of the following rules would you use?
A)Both the combinations rule and the basic counting rule
B)The combinations rule only
C)Both the permutations rule and the basic counting rule
D)The basic counting rule only

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
10
Write the word or phrase that best completes each statement or answers the question.
Give an example of a collection of events that are both mutually exclusive and exhaustive
Give an example of a collection of events that are both mutually exclusive and exhaustive

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
11
Write the word or phrase that best completes each statement or answers the question.
The following contingency table provides a joint frequency distribution for the popular
votes cast in the 1984 presidential election by region and political party. Data are in
thousands, rounded to the nearest thousand.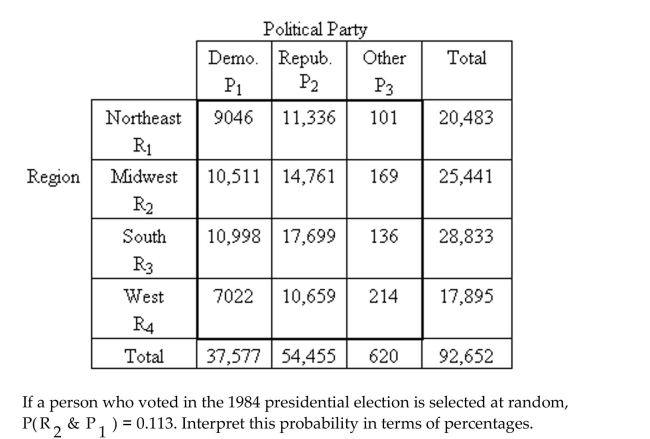
The following contingency table provides a joint frequency distribution for the popular
votes cast in the 1984 presidential election by region and political party. Data are in
thousands, rounded to the nearest thousand.


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
12
Write the word or phrase that best completes each statement or answers the question.
Define mutually exclusive events and independent events. Give an example of each.
Define mutually exclusive events and independent events. Give an example of each.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
13
Write the word or phrase that best completes each statement or answers the question.
A card is selected randomly from a standard deck of 52 cards. Let
A = event that the card is an ace.
Give examples of events B, C, and D such that A and B are independent, A and C are
dependent but not mutually exclusive, and A and D are mutually exclusive.
A card is selected randomly from a standard deck of 52 cards. Let
A = event that the card is an ace.
Give examples of events B, C, and D such that A and B are independent, A and C are
dependent but not mutually exclusive, and A and D are mutually exclusive.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
14
Write the word or phrase that best completes each statement or answers the question.
On an exam question asking for a probability, Sue had an answer of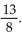 . Explain how she
. Explain how she
knew that this result was incorrect.
On an exam question asking for a probability, Sue had an answer of
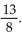 . Explain how she
. Explain how sheknew that this result was incorrect.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
15
Provide an appropriate response.
Consider the following counting problem. How many different sequences of 3 letters can be formed using the letters a, b, c, d, e if repetition is allowed?
To solve this problem which of the following rules would you use?
A)The basic counting rule only
B)The combinations rule only
C)Both the permutations rule and the basic counting rule
D)The permutations rule only
Consider the following counting problem. How many different sequences of 3 letters can be formed using the letters a, b, c, d, e if repetition is allowed?
To solve this problem which of the following rules would you use?
A)The basic counting rule only
B)The combinations rule only
C)Both the permutations rule and the basic counting rule
D)The permutations rule only

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
16
Write the word or phrase that best completes each statement or answers the question.
An experiment consists of randomly selecting a card from a deck of 52. The event A is
defined as follows.
A = event the card selected is a diamond
Give an example of an event B for this experiment such that the events A and B are
mutually exclusive.
An experiment consists of randomly selecting a card from a deck of 52. The event A is
defined as follows.
A = event the card selected is a diamond
Give an example of an event B for this experiment such that the events A and B are
mutually exclusive.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
17
Write the word or phrase that best completes each statement or answers the question.
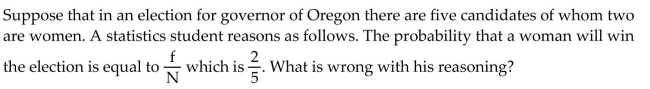
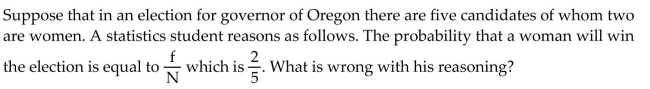

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
18
Write the word or phrase that best completes each statement or answers the question.
Interpret the following probability statement using the frequentist interpretation of
probability. The probability is 0.83 that this particular type of surgery will be successful.
Interpret the following probability statement using the frequentist interpretation of
probability. The probability is 0.83 that this particular type of surgery will be successful.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
19
Write the word or phrase that best completes each statement or answers the question.
What important question must you answer before computing an "or" probability? How
does the answer influence your computation?
What important question must you answer before computing an "or" probability? How
does the answer influence your computation?

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
20
Write the word or phrase that best completes each statement or answers the question.
The following contingency table provides a joint frequency distribution for the popular
votes cast in the presidential election by region and political party. Data are in thousands,
rounded to the nearest thousand.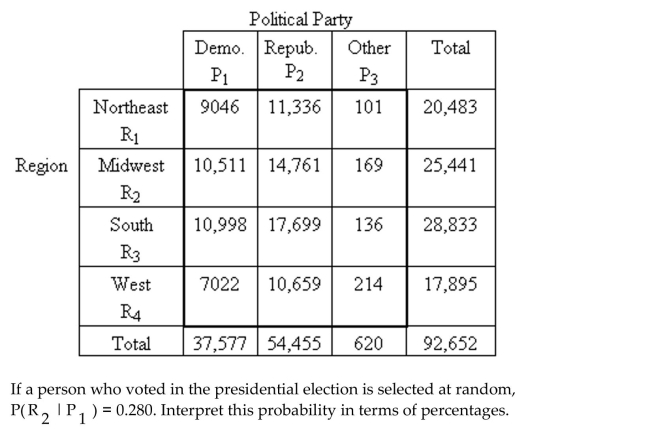
The following contingency table provides a joint frequency distribution for the popular
votes cast in the presidential election by region and political party. Data are in thousands,
rounded to the nearest thousand.


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
21
Write the word or phrase that best completes each statement or answers the question.
Describe an event whose probability of occurring is 1 and explain what that probability
means. Describe an event whose probability of occurring is 0 and explain what that
probability means.
Describe an event whose probability of occurring is 1 and explain what that probability
means. Describe an event whose probability of occurring is 0 and explain what that
probability means.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
22
Find the indicated probability by using the complementation rule.
The distribution of B.A. degrees conferred by a local college is listed below, by major.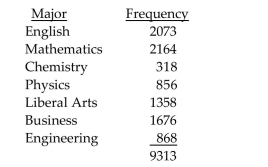 What is the probability that a randomly selected degree is not in Mathematics?
What is the probability that a randomly selected degree is not in Mathematics?
A)0.303
B)0.682
C)0.768
D)0.232
The distribution of B.A. degrees conferred by a local college is listed below, by major.
 What is the probability that a randomly selected degree is not in Mathematics?
What is the probability that a randomly selected degree is not in Mathematics?A)0.303
B)0.682
C)0.768
D)0.232

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
23
Write the word or phrase that best completes each statement or answers the question.
Suppose a student is taking a 5-response multiple choice exam; that is, the choices are A, B,
C, D, and E, with only one of the responses correct. Describe the complement method for
determining the probability of getting at least one of the questions correct on the
15-question exam. Why would the complement method be the method of choice for this
problem?
Suppose a student is taking a 5-response multiple choice exam; that is, the choices are A, B,
C, D, and E, with only one of the responses correct. Describe the complement method for
determining the probability of getting at least one of the questions correct on the
15-question exam. Why would the complement method be the method of choice for this
problem?

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
24
Write the word or phrase that best completes each statement or answers the question.
Construct a Venn diagram representing the event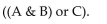
Construct a Venn diagram representing the event
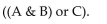

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
25
Write the word or phrase that best completes each statement or answers the question.
Discuss the differences, both in applications and in the formulas, for combinations and
permutations. Give an example of each.
Discuss the differences, both in applications and in the formulas, for combinations and
permutations. Give an example of each.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
26
Write the word or phrase that best completes each statement or answers the question.
The following contingency table provides a joint frequency distribution for the popular
votes cast in the presidential election by region and political party. Data are in thousands,
rounded to the nearest thousand.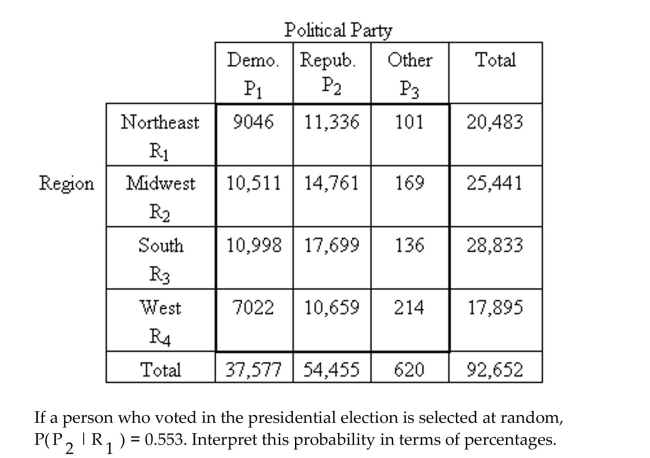
The following contingency table provides a joint frequency distribution for the popular
votes cast in the presidential election by region and political party. Data are in thousands,
rounded to the nearest thousand.


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the problem.
A poker hand consists of 5 cards dealt from an ordinary deck of 52 playing cards. How many different hands are there consisting of four cards of one suit and one card of another suit?
A)37,180
B)9295
C)111,540
D)715
A poker hand consists of 5 cards dealt from an ordinary deck of 52 playing cards. How many different hands are there consisting of four cards of one suit and one card of another suit?
A)37,180
B)9295
C)111,540
D)715

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
28
Use the rule of total probability to find the indicated probability.
A company is conducting a sweepstakes, and ships two boxes of game pieces to a particular store. Box A has 4% of its contents being winners, while 6% of the contents of box B are winners. Box A
Contains 34% of the total tickets. If the contents of both boxes are mixed in a drawer and a ticket is
Chosen at random, what is the probability it is a winner?
A)0.1
B)0.053
C)0.05
D)0.014
A company is conducting a sweepstakes, and ships two boxes of game pieces to a particular store. Box A has 4% of its contents being winners, while 6% of the contents of box B are winners. Box A
Contains 34% of the total tickets. If the contents of both boxes are mixed in a drawer and a ticket is
Chosen at random, what is the probability it is a winner?
A)0.1
B)0.053
C)0.05
D)0.014

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
29
The age distribution of students at a community college is given below.
A student from the community college is selected at random. Find the probability that the student is under 37 years old. Give your answer as a decimal rounded to three decimal places.
A)0.099
B)0.901
C)0.036
D)0.068
A student from the community college is selected at random. Find the probability that the student is under 37 years old. Give your answer as a decimal rounded to three decimal places.
A)0.099
B)0.901
C)0.036
D)0.068

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
30
Determine whether the events are independent.
The following contingency table provides a joint frequency distribution for a random sample of patients at a hospital classified by blood type and sex.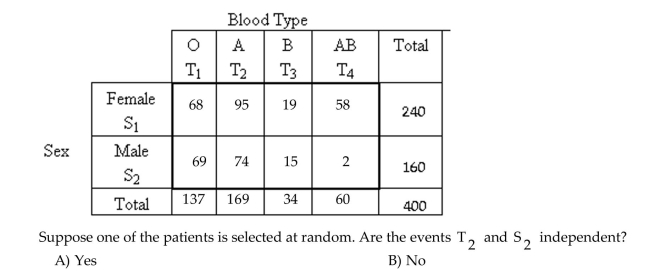
The following contingency table provides a joint frequency distribution for a random sample of patients at a hospital classified by blood type and sex.


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
31
Write the word or phrase that best completes each statement or answers the question.
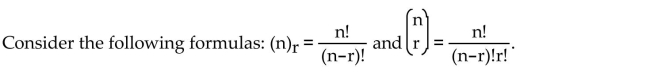 Given the same values for n and r in each formula, which is the smaller value, P or C? How
Given the same values for n and r in each formula, which is the smaller value, P or C? How
does this relate to the concept of counting the number of outcomes based on whether or not
order is a criterion?
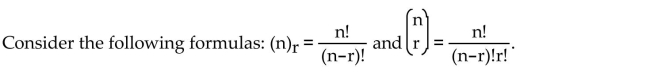 Given the same values for n and r in each formula, which is the smaller value, P or C? How
Given the same values for n and r in each formula, which is the smaller value, P or C? Howdoes this relate to the concept of counting the number of outcomes based on whether or not
order is a criterion?

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
32
Describe the specified event in words.
The number of hours needed by sixth grade students to complete a research project was recorded with the following results.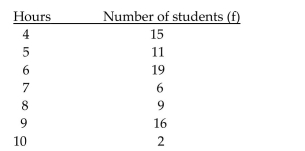 A student is selected at random. The event A is defined as follows.
A student is selected at random. The event A is defined as follows.
A = the event the student took between 5 and
9 hours inclusive
B = the event the student took at least 6 hours
Describe the event (A &
A)The event the student took between 6 and 9 hours inclusive
B)The event the student took between 5 and 6 hours inclusive
B)in words.
C)The event the student at least 5 hours
D)The event the student took more than 6 hours and less than 9 hours
The number of hours needed by sixth grade students to complete a research project was recorded with the following results.
 A student is selected at random. The event A is defined as follows.
A student is selected at random. The event A is defined as follows.A = the event the student took between 5 and
9 hours inclusive
B = the event the student took at least 6 hours
Describe the event (A &
A)The event the student took between 6 and 9 hours inclusive
B)The event the student took between 5 and 6 hours inclusive
B)in words.
C)The event the student at least 5 hours
D)The event the student took more than 6 hours and less than 9 hours

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
33
Find the indicated probability.
The following contingency table provides a joint frequency distribution for the popular votes cast in the presidential election by region and political party. Data are in thousands, rounded to the
Nearest thousand.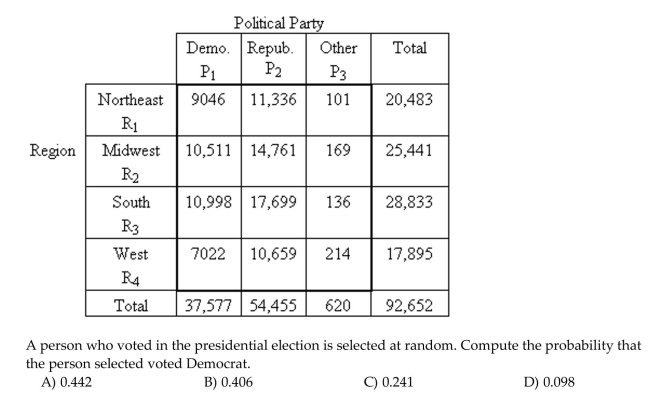
The following contingency table provides a joint frequency distribution for the popular votes cast in the presidential election by region and political party. Data are in thousands, rounded to the
Nearest thousand.


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
34
Find the indicated probability by using the special addition rule.
The distribution of B.A. degrees conferred by a local college is listed below, by major. What is the probability that a randomly selected degree is in English or Mathematics?
What is the probability that a randomly selected degree is in English or Mathematics?
A)0.455
B)0.424
C)0.010
D)0.517
The distribution of B.A. degrees conferred by a local college is listed below, by major.
 What is the probability that a randomly selected degree is in English or Mathematics?
What is the probability that a randomly selected degree is in English or Mathematics?A)0.455
B)0.424
C)0.010
D)0.517

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
35
Write the word or phrase that best completes each statement or answers the question.
Suppose that you roll a die and record the number that comes up and then flip a coin and
record whether it comes up heads or tails. One possible outcome can be represented as 2H
(a two on the die followed by heads). Make a list of all the possible outcomes. What is the
probability that you get tails and an even number? What assumption are you making
when you find this probability?
Suppose that you roll a die and record the number that comes up and then flip a coin and
record whether it comes up heads or tails. One possible outcome can be represented as 2H
(a two on the die followed by heads). Make a list of all the possible outcomes. What is the
probability that you get tails and an even number? What assumption are you making
when you find this probability?

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
36
Write the word or phrase that best completes each statement or answers the question.
An experiment consists of randomly selecting a card from a deck of 52. The event A is
defined as follows.
A = event the card selected is a diamond
Give an example of a pair of events B and C for this experiment such that the events A and
B are mutually exclusive but the collection of events A, B, and C is not mutually exclusive.
An experiment consists of randomly selecting a card from a deck of 52. The event A is
defined as follows.
A = event the card selected is a diamond
Give an example of a pair of events B and C for this experiment such that the events A and
B are mutually exclusive but the collection of events A, B, and C is not mutually exclusive.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
37
Determine whether the events are independent.
In a local election, 53.4% of those aged under 40 and 47.3% of those aged over 40 vote in favor of a certain ballot measure. Are age and position on the ballot measure independent?
A)Yes
B)No
In a local election, 53.4% of those aged under 40 and 47.3% of those aged over 40 vote in favor of a certain ballot measure. Are age and position on the ballot measure independent?
A)Yes
B)No

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
38
Write the word or phrase that best completes each statement or answers the question.
A relative frequency distribution is given below for the size of families in one U.S. city. A family is selected at random. Find the probability that the size of the family is at most 6. Round approximations to three decimal places.
A family is selected at random. Find the probability that the size of the family is at most 6. Round approximations to three decimal places.
A)0.034
B)0.948
C)0.052
D)0.982
A relative frequency distribution is given below for the size of families in one U.S. city.
 A family is selected at random. Find the probability that the size of the family is at most 6. Round approximations to three decimal places.
A family is selected at random. Find the probability that the size of the family is at most 6. Round approximations to three decimal places.A)0.034
B)0.948
C)0.052
D)0.982

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
39
Write the word or phrase that best completes each statement or answers the question.
Construct a Venn diagram portraying three events A, B, and C such that A and B are
mutually exclusive, B and C are mutually exclusive, but the collection of events A, B, and C
is not mutually exclusive.
Construct a Venn diagram portraying three events A, B, and C such that A and B are
mutually exclusive, B and C are mutually exclusive, but the collection of events A, B, and C
is not mutually exclusive.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
40
Find the indicated probability by using the special addition rule.
A relative frequency distribution is given below for the size of families in one U.S. city.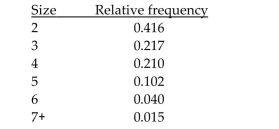 A family is selected at random. Find the probability that the size of the family is between 2 and 5 inclusive. Round approximations to three decimal places.
A family is selected at random. Find the probability that the size of the family is between 2 and 5 inclusive. Round approximations to three decimal places.
A)0.843
B)0.945
C)0.518
D)0.427
A relative frequency distribution is given below for the size of families in one U.S. city.
 A family is selected at random. Find the probability that the size of the family is between 2 and 5 inclusive. Round approximations to three decimal places.
A family is selected at random. Find the probability that the size of the family is between 2 and 5 inclusive. Round approximations to three decimal places.A)0.843
B)0.945
C)0.518
D)0.427

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
41
List the outcomes comprising the specified event.
When a quarter is tossed four times, 16 outcomes are possible.
When a quarter is tossed four times, 16 outcomes are possible.


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
42
Use the basic counting rule to solve the problem.
License plates are made using 2 letters followed by 2 digits. How many plates can be made if repetition of letters and digits is allowed?
A)10,000
B)67,600
C)456,976
D)6760
License plates are made using 2 letters followed by 2 digits. How many plates can be made if repetition of letters and digits is allowed?
A)10,000
B)67,600
C)456,976
D)6760

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
43
Use Bayes's rule to find the indicated probability.
Two shipments of components were received by a factory and stored in two separate bins. Shipment I has 2% of its contents defective, while shipment II has 5% of its contents defective. If it is
Equally likely an employee will go to either bin and select a component randomly, what is the
Probability that a defective component came from shipment II?
A)0.333
B)0.25
C)0.5
D)0.714
Two shipments of components were received by a factory and stored in two separate bins. Shipment I has 2% of its contents defective, while shipment II has 5% of its contents defective. If it is
Equally likely an employee will go to either bin and select a component randomly, what is the
Probability that a defective component came from shipment II?
A)0.333
B)0.25
C)0.5
D)0.714

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
44
Use the basic counting rule to solve the problem.
Mark can remember only the first 3 digits of his friend's phone number. He also knows that the number has 7 digits and that the last digit is not a 0. If Mark were to dial all of the possible numbers
And if it takes him 24 seconds to try each one, how long would it take to try every possibility?
A)400.1 minutes
B)3600 minutes
C)16 minutes
D)4000.8 minutes
Mark can remember only the first 3 digits of his friend's phone number. He also knows that the number has 7 digits and that the last digit is not a 0. If Mark were to dial all of the possible numbers
And if it takes him 24 seconds to try each one, how long would it take to try every possibility?
A)400.1 minutes
B)3600 minutes
C)16 minutes
D)4000.8 minutes

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
45
Use the special multiplication rule to find the indicated probability.
A family has five children. The probability of having a girl is 1/2. What is the probability of having at least 4 girls?
A)0.3125
B)0.0313
C)0.1875
D)0.1563
A family has five children. The probability of having a girl is 1/2. What is the probability of having at least 4 girls?
A)0.3125
B)0.0313
C)0.1875
D)0.1563

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
46
Find the indicated probability by using the general addition rule.
When two balanced dice are rolled, there are 36 possible outcomes. Find the probability that either doubles are rolled or the sum of the dice is 4.
When two balanced dice are rolled, there are 36 possible outcomes. Find the probability that either doubles are rolled or the sum of the dice is 4.


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
47
Use Bayes's rule to find the indicated probability.
A person must select one of three boxes, each filled with clocks. The probability of box A being selected is 0.33, of box B being selected is 0.17, and of box C being selected is 0.5. The probability of
Finding a red clock in box A is 0.2, in box B is 0.4, and in box C is 0.9. A box is selected. Given that
The box contains a red clock, what is the probability that box A was chosen?
A)0.066
B)0.33
C)0.133
D)0.113
A person must select one of three boxes, each filled with clocks. The probability of box A being selected is 0.33, of box B being selected is 0.17, and of box C being selected is 0.5. The probability of
Finding a red clock in box A is 0.2, in box B is 0.4, and in box C is 0.9. A box is selected. Given that
The box contains a red clock, what is the probability that box A was chosen?
A)0.066
B)0.33
C)0.133
D)0.113

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
48
Use Bayes's rule to find the indicated probability.
Two stores sell a certain product. Store A has 40% of the sales, 3% of which are of defective items, and store B has 60% of the sales, 5% of which are of defective items. The difference in defective
Rates is due to different levels of pre-sale checking of the product. A person receives a defective
Item of this product as a gift. What is the probability it came from store B?
A)0.75
B)0.3
C)0.2857
D)0.7143
Two stores sell a certain product. Store A has 40% of the sales, 3% of which are of defective items, and store B has 60% of the sales, 5% of which are of defective items. The difference in defective
Rates is due to different levels of pre-sale checking of the product. A person receives a defective
Item of this product as a gift. What is the probability it came from store B?
A)0.75
B)0.3
C)0.2857
D)0.7143

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
49
Use Bayes's rule to find the indicated probability.
A survey conducted in one U.S. city together with information from the census bureau yielded the following table. The first two columns give a percentage distribution of adults in the city by ethnic
Group. The third column gives the percentage of people in each ethnic group who have health
Insurance.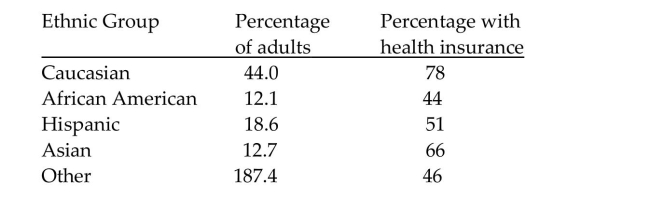 An adult is selected at random from the city. Determine the probability that the adult obtained is
An adult is selected at random from the city. Determine the probability that the adult obtained is
Asian given that he or she has health insurance.
A)0.001
B)0.084
C)0.66
D)0.127
A survey conducted in one U.S. city together with information from the census bureau yielded the following table. The first two columns give a percentage distribution of adults in the city by ethnic
Group. The third column gives the percentage of people in each ethnic group who have health
Insurance.
 An adult is selected at random from the city. Determine the probability that the adult obtained is
An adult is selected at random from the city. Determine the probability that the adult obtained isAsian given that he or she has health insurance.
A)0.001
B)0.084
C)0.66
D)0.127

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
50
Find the indicated probability.
In a batch of 8000 clock radios 7% are defective. A sample of 9 clock radios is randomly selected without replacement from the 8,000 and tested. The entire batch will be rejected if at least one of
Those tested is defective. What is the probability that the entire batch will be rejected?
A)0.111
B)0.520
C)0.480
D)0.0700
In a batch of 8000 clock radios 7% are defective. A sample of 9 clock radios is randomly selected without replacement from the 8,000 and tested. The entire batch will be rejected if at least one of
Those tested is defective. What is the probability that the entire batch will be rejected?
A)0.111
B)0.520
C)0.480
D)0.0700

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
51
Determine whether the events are mutually exclusive.
The number of hours needed by sixth grade students to complete a research project was recorded with the following results. A student is selected at random. The events A, B, and C are defined as follows.
A student is selected at random. The events A, B, and C are defined as follows.
A = event the student took more than 9 hours
B = event the student took less than 6 hours
C = event the student took between 7 and
9 hours inclusive
Is the collection of events A, B, and C mutually exclusive?
A)Yes
B)No
The number of hours needed by sixth grade students to complete a research project was recorded with the following results.
 A student is selected at random. The events A, B, and C are defined as follows.
A student is selected at random. The events A, B, and C are defined as follows.A = event the student took more than 9 hours
B = event the student took less than 6 hours
C = event the student took between 7 and
9 hours inclusive
Is the collection of events A, B, and C mutually exclusive?
A)Yes
B)No

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
52
Provide an appropriate response.
A person is selected at random from a certain population. Let A = event the person is left-handed
B = event the person is male.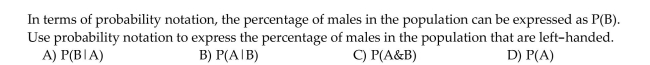
A person is selected at random from a certain population. Let A = event the person is left-handed
B = event the person is male.
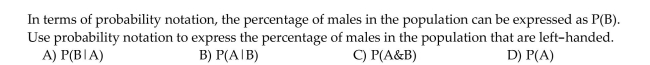

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
53
Describe the specified event in words.
The number of hours needed by sixth grade students to complete a research project was recorded with the following results. A student is selected at random. The event A is defined as follows.
A student is selected at random. The event A is defined as follows.
A = the event the student took at least 6 hours
Describe the event (not
A)The event the student took at most 6 hours
A)in words.
B)The event the student did not take 6 hours
C)The event the student took more than 6 hours
D)The event the student took less than 6 hours
The number of hours needed by sixth grade students to complete a research project was recorded with the following results.
 A student is selected at random. The event A is defined as follows.
A student is selected at random. The event A is defined as follows.A = the event the student took at least 6 hours
Describe the event (not
A)The event the student took at most 6 hours
A)in words.
B)The event the student did not take 6 hours
C)The event the student took more than 6 hours
D)The event the student took less than 6 hours

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
54
Find the conditional probability.
If two fair dice are rolled, find the probability of a sum of 6 given that the roll is a "double".
A)0.333
B)0.167
C)0.25
D)0.5
If two fair dice are rolled, find the probability of a sum of 6 given that the roll is a "double".
A)0.333
B)0.167
C)0.25
D)0.5

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
55
Use the rule of total probability to find the indicated probability.
A teacher designs a test so a student who studies will pass 82% of the time, but a student who does not study will pass 13% of the time. A certain student studies for 81% of the tests taken. On a given
Test, what is the probability that student passes?
A)0.664
B)0.247
C)0.689
D)0.475
A teacher designs a test so a student who studies will pass 82% of the time, but a student who does not study will pass 13% of the time. A certain student studies for 81% of the tests taken. On a given
Test, what is the probability that student passes?
A)0.664
B)0.247
C)0.689
D)0.475

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
56
Determine whether the events are independent.
The following contingency table provides a joint probability distribution for a random sample of patients at a hospital classified by blood type and
Sex.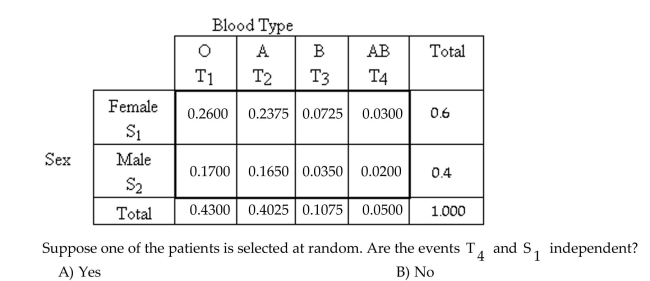
The following contingency table provides a joint probability distribution for a random sample of patients at a hospital classified by blood type and
Sex.


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
57
Use counting rules to determine the probability.
In a card game, each player is dealt 4 cards from an ordinary deck of 52 playing cards. Determine the probability of being dealt a hand containing three cards of one denomination and one of
Another.
A)0.0137
B)0.165
C)0.00922
D)0.0000591
In a card game, each player is dealt 4 cards from an ordinary deck of 52 playing cards. Determine the probability of being dealt a hand containing three cards of one denomination and one of
Another.
A)0.0137
B)0.165
C)0.00922
D)0.0000591

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
58
Use words or symbols, as indicated, to describe the event.
The following contingency table provides a joint frequency distribution for the popular votes cast in the presidential election by region and political party. Data are in thousands, rounded to the
Nearest thousand.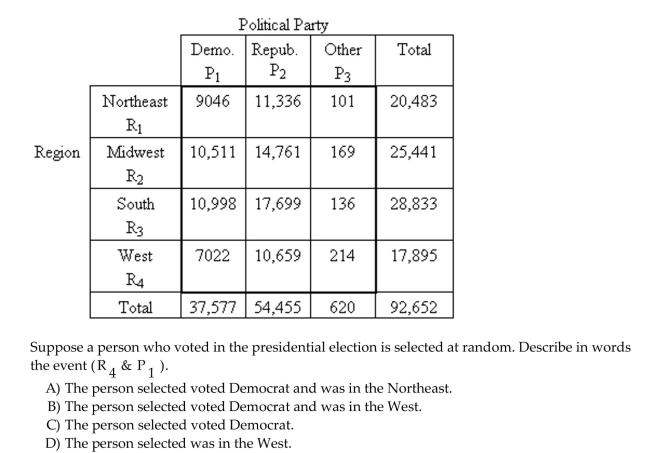
The following contingency table provides a joint frequency distribution for the popular votes cast in the presidential election by region and political party. Data are in thousands, rounded to the
Nearest thousand.


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
59
Determine the number of outcomes that comprise the specified event.
The number of hours needed by sixth grade students to complete a research project was recorded with the following results.
The number of hours needed by sixth grade students to complete a research project was recorded with the following results.


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
60
Use counting rules to determine the probability.
A tourist in France wants to visit 5 different cities. If the route is randomly selected, what is the probability that she will visit the cities in alphabetical order?
A)0.04
B)0.008
C)0.00833
D)0.2
A tourist in France wants to visit 5 different cities. If the route is randomly selected, what is the probability that she will visit the cities in alphabetical order?
A)0.04
B)0.008
C)0.00833
D)0.2

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
61
Find the indicated probability.
The following contingency table provides a joint frequency distribution for the popular votes cast in the presidential election by region and political party. Data are in thousands, rounded to the
Nearest thousand.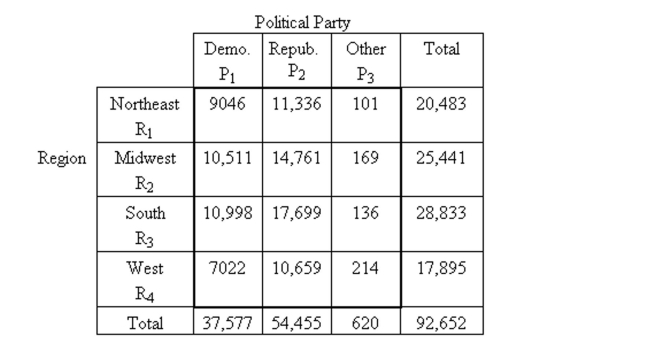 A person who voted in the presidential election is selected at random. Compute the probability that
A person who voted in the presidential election is selected at random. Compute the probability that
The person selected was in the West and voted Republican.
A)0.196
B)0.781
C)0.115
D)0.588
The following contingency table provides a joint frequency distribution for the popular votes cast in the presidential election by region and political party. Data are in thousands, rounded to the
Nearest thousand.
 A person who voted in the presidential election is selected at random. Compute the probability that
A person who voted in the presidential election is selected at random. Compute the probability thatThe person selected was in the West and voted Republican.
A)0.196
B)0.781
C)0.115
D)0.588

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
62
List the outcomes comprising the specified event.
When a quarter is tossed four times, 16 outcomes are possible.
When a quarter is tossed four times, 16 outcomes are possible.


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
63
Determine whether the events are independent.
When a coin is tossed three times, eight equally likely outcomes are possible. Are A and B independent events?
Are A and B independent events?
A)Yes
B)No
When a coin is tossed three times, eight equally likely outcomes are possible.
 Are A and B independent events?
Are A and B independent events?A)Yes
B)No

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
64
Draw a Venn diagram and shade the described events.
From a finite sample, events A and B are mutually exclusive. Shade the collection A or B.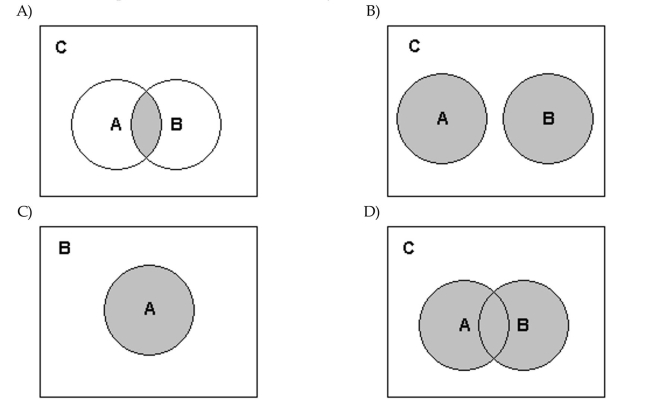
From a finite sample, events A and B are mutually exclusive. Shade the collection A or B.


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
65
Find the conditional probability.
The following contingency table provides a joint frequency distribution for a group of retired people by career and age at retirement.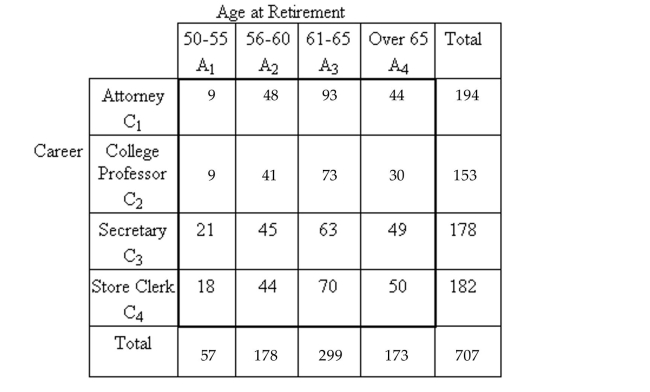 Suppose one of these people is selected at random. Compute the probability that the person's age of
Suppose one of these people is selected at random. Compute the probability that the person's age of
Retirement was between 50 and 55 given that he or she was an attorney.
A)0.081
B)0.013
C)0.158
D)0.046
The following contingency table provides a joint frequency distribution for a group of retired people by career and age at retirement.
 Suppose one of these people is selected at random. Compute the probability that the person's age of
Suppose one of these people is selected at random. Compute the probability that the person's age ofRetirement was between 50 and 55 given that he or she was an attorney.
A)0.081
B)0.013
C)0.158
D)0.046

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
66
Use counting rules to determine the probability.
A committee of 11 members is voting on a proposal. Each member casts a yea or nay vote. On a random voting basis, what is the probability that the proposal wins by a vote of 8 to 3?
A)0.16113
B)0.08057
C)0.03833
D)0.04028
A committee of 11 members is voting on a proposal. Each member casts a yea or nay vote. On a random voting basis, what is the probability that the proposal wins by a vote of 8 to 3?
A)0.16113
B)0.08057
C)0.03833
D)0.04028

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
67
Provide an appropriate response.
A contingency table provides a joint frequency distribution for the popular votes cast in a
presidential election by sex and political party. A joint probability distribution corresponding to the
contingency table is obtained and can be represented as follows.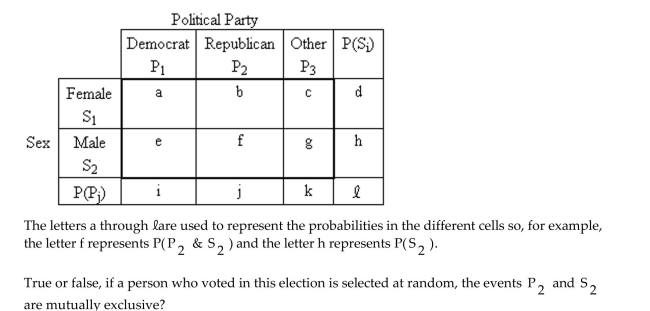
A contingency table provides a joint frequency distribution for the popular votes cast in a
presidential election by sex and political party. A joint probability distribution corresponding to the
contingency table is obtained and can be represented as follows.


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
68
List the outcomes comprising the specified event.
When a quarter is tossed four times, 16 outcomes are possible.
When a quarter is tossed four times, 16 outcomes are possible.


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
69
Use counting rules to determine the probability.
Dave puts a collection of 15 books on a bookshelf in a random order. Among the books are 2 fiction and 13 nonfiction books. What is the probability that the 2 fiction books will be all together on the
Left side of the shelf and the 13 nonfiction all together on the right side of the shelf?
A)0.00952
B)0.01809
C)0.01333
D)0.01619
Dave puts a collection of 15 books on a bookshelf in a random order. Among the books are 2 fiction and 13 nonfiction books. What is the probability that the 2 fiction books will be all together on the
Left side of the shelf and the 13 nonfiction all together on the right side of the shelf?
A)0.00952
B)0.01809
C)0.01333
D)0.01619

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the problem.
A poker hand consists of 5 cards dealt from an ordinary deck of 52 playing cards. How many different hands are there consisting of four hearts and one spade?
A)13
B)728
C)715
D)9295
A poker hand consists of 5 cards dealt from an ordinary deck of 52 playing cards. How many different hands are there consisting of four hearts and one spade?
A)13
B)728
C)715
D)9295

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
71
Use the special multiplication rule to find the indicated probability.
A family has five children. The probability of having a girl is 1/2. What is the probability of having 3 girls followed by 2 boys?
A)0.0313
B)0.0625
C)0.3125
D)0.6252
A family has five children. The probability of having a girl is 1/2. What is the probability of having 3 girls followed by 2 boys?
A)0.0313
B)0.0625
C)0.3125
D)0.6252

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
72
Determine whether the events are independent.
An auto insurance company was interested in investigating accident rates for drivers in different age groups. The following contingency table was based on a random sample of drivers and
Classifies drivers by age group and number of accidents in the past three years.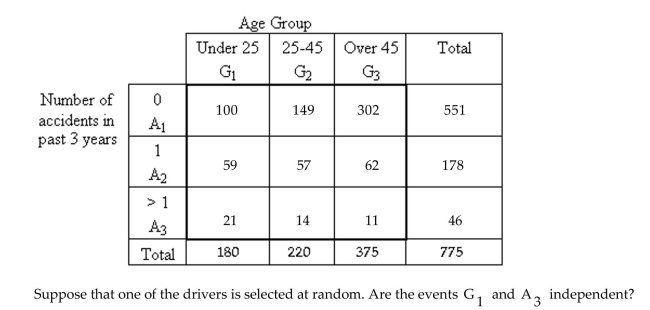
A)Yes
B)No
An auto insurance company was interested in investigating accident rates for drivers in different age groups. The following contingency table was based on a random sample of drivers and
Classifies drivers by age group and number of accidents in the past three years.

A)Yes
B)No

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
73
Find the indicated probability by using the general addition rule.



Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
74
Use the rule of total probability to find the indicated probability.
Among students at one college are 3874 women and 3058 men. The following table provides relative-frequency distributions for subject major for males and females at the college.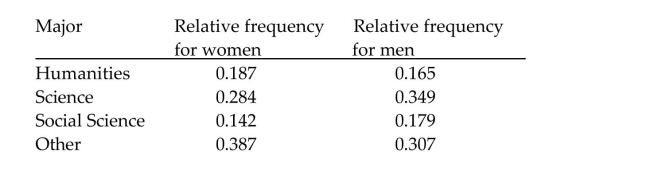 A student is selected at random from the college. Determine the probability that the student is a
A student is selected at random from the college. Determine the probability that the student is a
Science major.
A)0.317
B)0.159
C)0.313
D)0.320
Among students at one college are 3874 women and 3058 men. The following table provides relative-frequency distributions for subject major for males and females at the college.
 A student is selected at random from the college. Determine the probability that the student is a
A student is selected at random from the college. Determine the probability that the student is aScience major.
A)0.317
B)0.159
C)0.313
D)0.320

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
75
Provide an appropriate response.
A contingency table provides a joint frequency distribution for the popular votes cast in a
presidential election by sex and political party. A joint probability distribution corresponding to the
contingency table is obtained and can be represented as follows.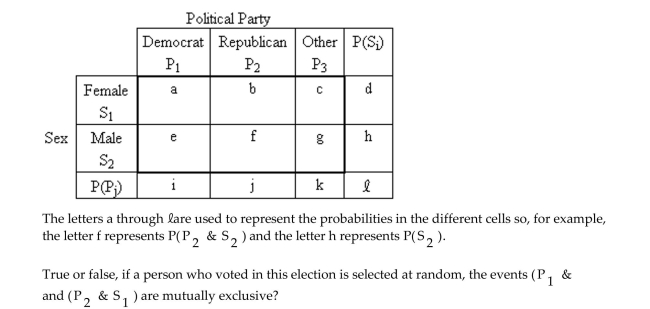
A contingency table provides a joint frequency distribution for the popular votes cast in a
presidential election by sex and political party. A joint probability distribution corresponding to the
contingency table is obtained and can be represented as follows.


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
76
Find the indicated probability.
The Book Industry Study Group, Inc., performs sample surveys to obtain information on characteristics of book readers. A book reader is defined to be one who read one or more books
In the six months prior to the survey; a non-book reader is defined to be one who read
Newspapers or magazines but no books in the six months prior to the survey; a nonreader is
Defined to be one who did not read a book, newspaper, or magazine in the six months prior to
The survey.
The following data were obtained from a random sample of people 16 years old and over.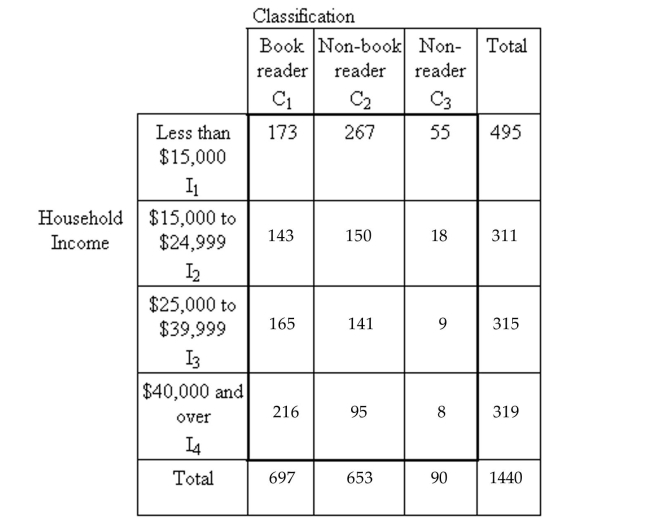 Suppose one of these people is selected at random. Compute the probability that the person is a
Suppose one of these people is selected at random. Compute the probability that the person is a
Nonreader.
A)0.062
B)0.611
C)0.111
D)0.038
The Book Industry Study Group, Inc., performs sample surveys to obtain information on characteristics of book readers. A book reader is defined to be one who read one or more books
In the six months prior to the survey; a non-book reader is defined to be one who read
Newspapers or magazines but no books in the six months prior to the survey; a nonreader is
Defined to be one who did not read a book, newspaper, or magazine in the six months prior to
The survey.
The following data were obtained from a random sample of people 16 years old and over.
 Suppose one of these people is selected at random. Compute the probability that the person is a
Suppose one of these people is selected at random. Compute the probability that the person is aNonreader.
A)0.062
B)0.611
C)0.111
D)0.038

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
77
Use the special multiplication rule to find the indicated probability.
In one large city, 42% of all voters are Democrats. If two voters are randomly selected for a survey, find the probability that they are both Democrats.
A)0.176
B)0.420
C)0.172
D)0.840
In one large city, 42% of all voters are Democrats. If two voters are randomly selected for a survey, find the probability that they are both Democrats.
A)0.176
B)0.420
C)0.172
D)0.840

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
78
Use counting rules to determine the probability.
A student takes a true-false test consisting of 12 questions. Assuming that the student guesses at each question, find the probability that the student answers exactly 10 questions correctly.
A)0.0129
B)0.0161
C)0.0097
D)0.0064
A student takes a true-false test consisting of 12 questions. Assuming that the student guesses at each question, find the probability that the student answers exactly 10 questions correctly.
A)0.0129
B)0.0161
C)0.0097
D)0.0064

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
79
Use the special multiplication rule to find the indicated probability.
In one large city, 63% of adults have health insurance. What is the probability that 4 adults selected at random from the town all have health insurance?
A)0.158
B)2.52
C)0.63
D)0.063
In one large city, 63% of adults have health insurance. What is the probability that 4 adults selected at random from the town all have health insurance?
A)0.158
B)2.52
C)0.63
D)0.063

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
80
Determine whether the events are independent.
When a balanced die is rolled twice, 36 equally likely outcomes are possible. Let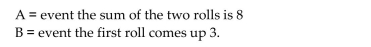 Are A and B independent events?
Are A and B independent events?
A)Yes
B)No
When a balanced die is rolled twice, 36 equally likely outcomes are possible. Let
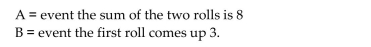 Are A and B independent events?
Are A and B independent events?A)Yes
B)No

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck


