Exam 4: Probability Concepts

Find the indicated probability by using the general addition rule. -Let $\mathrm { A }$ and $\mathrm { B }$ be events such that $\mathrm { P } ( \mathrm { A } ) = \frac { 1 } { 7 } , \mathrm { P } ( \mathrm { A }$ or $\mathrm { B } ) = \frac { 1 } { 6 }$ , and $\mathrm { P } ( \mathrm { A }$ and $\mathrm { B } ) = \frac { 1 } { 12 }$ . Determine $\mathrm { P } ( \mathrm { B } )$ .

Use the basic counting rule to solve the problem. -A singer-songwriter wishes to compose a melody. Each note in the melody must be one of the 12 notes in her vocal range. How many different sequences of 4 notes are possible?

Use the special multiplication rule to find the indicated probability. -In one large city, 42% of all voters are Democrats. If two voters are randomly selected for a survey, find the probability that they are both Democrats.

List the outcomes comprising the specified event. -Three board members for a nonprofit organization will be selected from a group of five people. The board members will be selected by drawing names from a hat. The names of the five possible board Members are Allison, Bob, Charlie, Dave, and Emily. The possible outcomes can be represented as Follows. Here, for example, $\mathrm { ABC }$ represents the outcome that Allison, Bob, and Charlie are selected to be on the board. The event $\mathrm { A }$ is defined as follows. $A =$ event that Bob and Dave are both selected List the outcomes that comprise the event (not A).

Use the rule of total probability to find the indicated probability. -A company is conducting a sweepstakes, and ships two boxes of game pieces to a particular store. Box A has 4% of its contents being winners, while 6% of the contents of box B are winners. Box A Contains 34% of the total tickets. If the contents of both boxes are mixed in a drawer and a ticket is Chosen at random, what is the probability it is a winner?

Determine the number of outcomes that comprise the specified event. -The number of hours needed by sixth grade students to complete a research project was recorded with the following results. Hours Number of students (f) 4 24 5 16 6 27 7 13 8 11 9 4 10+ 8 A student is selected at random. The events A and B are defined as follows. $\mathrm { A } =$ the event the student took at most 8 hours $B =$ the event the student took at least 8 hours Determine the number of outcomes that comprise the event (A or B).

Find the indicated probability. -If two balanced die are rolled, the possible outcomes can be represented as follows. $( 1,1 ) ( 2,1 ) ( 3,1 ) ( 4,1 ) ( 5,1 ) ( 6,1 )$ $( 1,2 ) ( 2,2 ) ( 3,2 ) ( 4,2 ) ( 5,2 ) ( 6,2 )$ $( 1,3 ) ( 2,3 ) ( 3,3 ) ( 4,3 ) ( 5,3 ) ( 6,3 )$ $( 1,4 ) ( 2,4 ) ( 3,4 ) ( 4,4 ) ( 5,4 ) ( 6,4 )$ $( 1,5 ) ( 2,5 ) ( 3,5 ) ( 4,5 ) ( 5,5 ) ( 6,5 )$ $( 1,6 ) ( 2,6 ) ( 3,6 ) ( 4,6 ) ( 5,6 ) ( 6,6 )$ Determine the probability that the sum of the dice is 3 or 9 .

Use words or symbols, as indicated, to describe the event. -The Book Industry Study Group, Inc., performs sample surveys to obtain information on characteristics of book readers. A book reader is defined to be one who read one or more books in The six months prior to the survey; a non-book reader is defined to be one who read newspapers or Magazines but no books in the six months prior to the survey; a nonreader is defined to be one who Did not read a book, newspaper, or magazine in the six months prior to the survey. The following Data were obtained from a random sample of 1429 persons 16 years old and over. 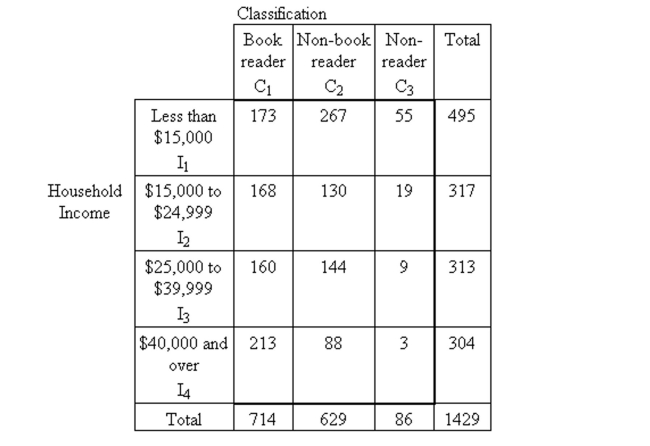How may people made less than $40,000?

Determine the number of outcomes that comprise the specified event. -The number of hours needed by sixth grade students to complete a research project was recorded with the following results. Hours Number of students (f) 4 25 5 25 6 24 7 10 8 14 9 6 10+ 5 A student is selected at random. The event $\mathrm { A }$ is defined as follows. $\mathrm { A } =$ the event the student took more than 7 hours Determine the number of outcomes that comprise the event (not A).

Find the indicated probability. -In a batch of 8000 clock radios 7% are defective. A sample of 9 clock radios is randomly selected without replacement from the 8,000 and tested. The entire batch will be rejected if at least one of Those tested is defective. What is the probability that the entire batch will be rejected?

Use the basic counting rule to solve the problem. -Mark can remember only the first 3 digits of his friend's phone number. He also knows that the number has 7 digits and that the last digit is not a 0. If Mark were to dial all of the possible numbers And if it takes him 24 seconds to try each one, how long would it take to try every possibility?

Find the conditional probability. -The age distribution of students at a community college is given below. Age (years) Number of students (f) Under 21 416 21-25 420 26-30 219 31-35 51 Over 35 24 1130 A student from the community college is selected at random. Find the conditional probability that the student is between 26 and 30 given that he or she is at least

Determine whether the events are independent. -In a local election, 53.4% of those aged under 40 and 47.3% of those aged over 40 vote in favor of a certain ballot measure. Are age and position on the ballot measure independent?

Use the special multiplication rule to find the indicated probability. -A family has five children. The probability of having a girl is 1/2. What is the probability of having 3 girls followed by 2 boys?

The following contingency table provides a joint frequency distribution for the popular votes cast in the presidential election by region and political party. Data are in thousands, rounded to the nearest thousand. 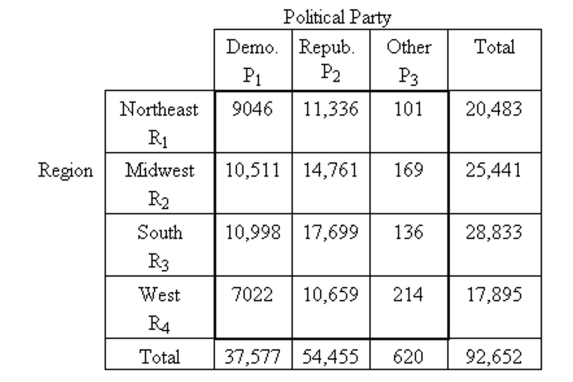If a person who voted in the presidential election is selected at random, $\mathrm { P } \left( \mathrm { P } _ { 2 } \mid \mathrm { R } _ { 1 } \right) = 0.553$ . Interpret this probability in terms of percentages.

Find the indicated probability by using the general addition rule. -Of the 94 people who answered "yes" to a question, 6 were male. Of the 54 people who answered "no" to the question, 12 were male. If one person is selected at random from the group, what is the Probability that the person answered "yes" or was male?

Determine whether the events are independent. -When a coin is tossed three times, eight equally likely outcomes are possible. HHH HHT HTH HTT THH THT TTH TTT Let $\mathrm { A } =$ event the first two tosses are the same $B =$ event the last two tosses are the same. Are A and B independent events?

Consider the following counting problem. How many different sequences of 3 letters can be formed using the letters a, b, c, d, e if repetition is allowed? To solve this problem which of the following rules would you use?

List the outcomes comprising the specified event. -When a quarter is tossed four times, 16 outcomes are possible. HHHH HHHT HHTH HHTT HTHH HTHT HTTH HTTT THHH THHT THTH THTT TTHH TTHT TTTH TTTT Here, for example, HTTH represents the outcome that the first toss is heads, the next two tosses are tails, and the fourth toss is heads. The events $A$ and $B$ are defined as follows. $\mathrm { A } =$ event exactly two tails are tossed $B =$ event the first and last tosses are the same List the outcomes that comprise the event (A & B).

Use the special multiplication rule to find the indicated probability. -In one large city, 63% of adults have health insurance. What is the probability that 4 adults selected at random from the town all have health insurance?