Deck 8: Sequences, Series, and Combinatorics
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/92
Play
Full screen (f)
Deck 8: Sequences, Series, and Combinatorics
1
Find the sum, if it exists.
A) 2460
B) 93
C) 1452
D) Does not exist
A) 2460
B) 93
C) 1452
D) Does not exist
C
2
Use mathematical induction to prove the following.
3
Find fraction notation.
A)
B)
C)
D)
A)
B)
C)
D)
B
4
Use mathematical induction to prove the following.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
5
Find the sum, if it exists.
A)
B)
C)
D) Does not exist
A)
B)
C)
D) Does not exist

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
6
Evaluate.
A) 1722
B)
C) 126
D) 68,880
A) 1722
B)
C) 126
D) 68,880

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
7
Use mathematical induction to prove the following.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
8
Use mathematical induction to prove the following.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
9
Use mathematical induction to prove the following.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
10
Use mathematical induction to prove the following.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
11
Use mathematical induction to prove the following.
If a is a constant and 0 < a < 1, then an < 1.
If a is a constant and 0 < a < 1, then an < 1.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
12
Find the indicated term of the binomial expansion.
6th term;
A)
B)
C)
D)
6th term;
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
13
Use mathematical induction to prove the following.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
14
Use mathematical induction to prove the following.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
15
Use mathematical induction to prove the following.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
16
For the given arithmetic series, what is
, and
A) 8340
B) 2111
C) 4170
D) 2085
, and
A) 8340
B) 2111
C) 4170
D) 2085

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
17
Expand, where i
A) 8
B)
C)
D) 1
A) 8
B)
C)
D) 1

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
18
Write sigma notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
19
Use mathematical induction to prove the following.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
20
Use mathematical induction to prove the following.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
21
Find the first 4 terms of the recursively defined sequence.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
22
Find the nth, or general, term.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
23
Find the sum.
A) 81
B) 26
C) 6
D) 75
A) 81
B) 26
C) 6
D) 75

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
24
Evaluate the sum.
A) 202
B) 364
C) 355
D) 363
A) 202
B) 364
C) 355
D) 363

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
25
Find the nth, or general, term.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
26
Solve.
How many 2-letter codes can be formed with the letters P, Q, R, S, T without repetition?
A)20
B)4
C)10
D)40
How many 2-letter codes can be formed with the letters P, Q, R, S, T without repetition?
A)20
B)4
C)10
D)40

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
27
What term of the arithmetic sequence is the given number?
3.42, 3.57, 3.72, . . . ;5.97
A)17
B)16
C)15
D)18
3.42, 3.57, 3.72, . . . ;5.97
A)17
B)16
C)15
D)18

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
28
Find the indicated term of the sequence.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
29
Find the indicated sum.
Find the sum of the first 13 terms of the geometric sequence:
A)
B) 1369
C)
D)
Find the sum of the first 13 terms of the geometric sequence:
A)
B) 1369
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
30
Evaluate.
A) 0 !
B) 4
C) 1
D) 6
A) 0 !
B) 4
C) 1
D) 6

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
31
Solve.
Find the sum of the first 114 positive multiples of 3.
A)19,323
B)19,665
C)19,494
D)19,838
Find the sum of the first 114 positive multiples of 3.
A)19,323
B)19,665
C)19,494
D)19,838

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the problem.
The population of a town was 25,400 at the beginning of 1970. If the population decreased 350 people per year, how many people lived in the town at the beginning of 1985?
A)19,800 people
B)20,150 people
C)5250 people
D)20,500 people
The population of a town was 25,400 at the beginning of 1970. If the population decreased 350 people per year, how many people lived in the town at the beginning of 1985?
A)19,800 people
B)20,150 people
C)5250 people
D)20,500 people

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
33
Find the sum, if it exists.
A)
B)
C)
D) Does not exist
A)
B)
C)
D) Does not exist

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
34
Expand, where i
A)
B)
C) 1
D)
A)
B)
C) 1
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
35
Determine the number of subsets of the set.
A set of 11 elements
A)2048
B)22
C)1024
D)23
A set of 11 elements
A)2048
B)22
C)1024
D)23

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
36
Write sigma notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
37
Evaluate.
A)
B) 10,080
C) 5040
D) 1
A)
B) 10,080
C) 5040
D) 1

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
38
Find the common ratio.
64, 32, 16, 8, 4, . . .
A)4
B)-0.5
C)2
D)0.5
64, 32, 16, 8, 4, . . .
A)4
B)-0.5
C)2
D)0.5

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
39
Find the indicated term.
; the 9 th term.
A)
B)
C) 64
D) 128
; the 9 th term.
A)
B)
C) 64
D) 128

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
40
Find fraction notation.
A) 0
B)
C)
D)
A) 0
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
41
Solve.
A sequence of yearly payments of $3000 is invested at the end of each of 9 years at an interest rate of 4.6%%, compounded annually. What is the total amount of the annuity after 9 years?
A)$32,539.77
B)$31,539.77
C)$33,539.77
D)$32,039.77
A sequence of yearly payments of $3000 is invested at the end of each of 9 years at an interest rate of 4.6%%, compounded annually. What is the total amount of the annuity after 9 years?
A)$32,539.77
B)$31,539.77
C)$33,539.77
D)$32,039.77

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
42
Find the indicated quantity.
, when and
A)
B) 9
C) 6
D) 12
, when and
A)
B) 9
C) 6
D) 12

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
43
Find the nth, or general, term.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the problem.
During a five-year period, a company doubles its profits each year. If the profits at the end of the fifth year are $224,000, then what are the profits for each of the first four years?
A)$14,000, $28,000, $42,000, $56,000
B)$14,000, $28,000, $56,000, $112,000
C)$15,000, $30,000, $60,000, $118,000
D)$14,000, $28,000, $56,000, $140,000
During a five-year period, a company doubles its profits each year. If the profits at the end of the fifth year are $224,000, then what are the profits for each of the first four years?
A)$14,000, $28,000, $42,000, $56,000
B)$14,000, $28,000, $56,000, $112,000
C)$15,000, $30,000, $60,000, $118,000
D)$14,000, $28,000, $56,000, $140,000

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
45
Evaluate the sum.
A) 1
B) 10
C) 11
D) 0
A) 1
B) 10
C) 11
D) 0

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
46
Evaluate.
A) 330
B) 3960
C) 792
D) 66
A) 330
B) 3960
C) 792
D) 66

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the problem.
An experiment was conducted. The results are listed in the following table. Use the table to determine which event has the greatest probability of occurring and what the probability of its occurrence is.
A)E; 0.296
B)D; 0.27
C)A; 0.228
D)D; 0.17
An experiment was conducted. The results are listed in the following table. Use the table to determine which event has the greatest probability of occurring and what the probability of its occurrence is.
A)E; 0.296
B)D; 0.27
C)A; 0.228
D)D; 0.17

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the problem.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
49
Find the indicated term of the sequence.
A) 5159
B) 3551
C) 4081
D) 4489
A) 5159
B) 3551
C) 4081
D) 4489

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
50
Determine how many of the first 5 statements in the sequence obtainable from the given statement are true.
The measure of each interior angle of a regular polygon with sides is .
A) 4
B) 5
C) 2
D) 3
The measure of each interior angle of a regular polygon with sides is .
A) 4
B) 5
C) 2
D) 3

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
51
Solve.
How many 4-letter codes can be formed with the letters A, B, C, D, E, F, G, H with repetition?
A)4096
B)336
C)240
D)56
How many 4-letter codes can be formed with the letters A, B, C, D, E, F, G, H with repetition?
A)4096
B)336
C)240
D)56

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
52
The nth term of a sequence is given. Find the first 4 terms.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
53
Find the common ratio.
A) 4
B) 20
C)
D)
A) 4
B) 20
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
54
Find the first 4 terms of the recursively defined sequence.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
55
For the given arithmetic series, what is
, and
A)
В)
C)
D)
, and
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
56
Find the indicated term of the binomial expansion.
7 th term;
A)
B)
C)
D)
7 th term;
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
57
Evaluate the sum.
A) 22
B) 14
C) 2
D)
A) 22
B) 14
C) 2
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
58
Solve the problem.
A) 19,380
B) 4845
C) 29,070
D) 116,280
A) 19,380
B) 4845
C) 29,070
D) 116,280

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
59
Solve.
Suppose 6 cards are drawn from a deck of 52 cards. What is the probability of drawing 3 spades and 3 hearts? A)
В)
C)
D)
Suppose 6 cards are drawn from a deck of 52 cards. What is the probability of drawing 3 spades and 3 hearts? A)
В)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
60
Expand.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
61
Expand.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
62
Find the sum, if it exists.
A)
B)
C)
D) Does not exist
A)
B)
C)
D) Does not exist

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
63
Evaluate.
A)
B) 5
C) 2 !
D) 20
A)
B) 5
C) 2 !
D) 20

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
64
Evaluate.
A) 210
B) 30
C)
D) 15
A) 210
B) 30
C)
D) 15

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
65
Find the first term and the common difference.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
66
Find the first term and the common difference.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
67
Solve.
A pendulum bob swings on its first oscillation. On each subsequent oscillation the bob travels of the previous distance. Find the total distance the bob travels before coming to rest.
A)
B)
C)
D)
A pendulum bob swings on its first oscillation. On each subsequent oscillation the bob travels of the previous distance. Find the total distance the bob travels before coming to rest.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
68
Expand.
A)
B) 370
C) 208
D) 416
A)
B) 370
C) 208
D) 416

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
69
Evaluate.
A) 6840
B)
C) 116,280
D)
A) 6840
B)
C) 116,280
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
70
What term of the arithmetic sequence is the given number?
A) 22
B) 21
C) 19
D) 20
A) 22
B) 21
C) 19
D) 20

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
71
Find the indicated term of the sequence.
A)
B)
C) 38,520
D) 37,440
A)
B)
C) 38,520
D) 37,440

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
72
Find the nth, or general, term.
1, 7, 49, . . . A)
В)
C)
D)
1, 7, 49, . . . A)
В)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
73
Solve the problem.
An experiment was conducted. The results are listed in the following table.
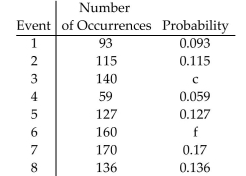
What are the values of c and f?
A)0.144, 0.16
B)0.16, 0.21
C)0.14, 0.16
D)0.14, 0.26
An experiment was conducted. The results are listed in the following table.

What are the values of c and f?
A)0.144, 0.16
B)0.16, 0.21
C)0.14, 0.16
D)0.14, 0.26

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
74
Find the indicated term of the binomial expansion.
5 th term;
A)
B)
C) 15,625
D)
5 th term;
A)
B)
C) 15,625
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
75
Find the indicated quantity.
, when and
A)
B) 36
C)
D)
, when and
A)
B) 36
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
76
Determine how many of the first 5 statements in the sequence obtainable from the given statement are true.
is a perfect square.
A) 4
B) 2
C) 3
D) 5
is a perfect square.
A) 4
B) 2
C) 3
D) 5

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
77
Find fraction notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
78
Determine how many of the first 5 statements in the sequence obtainable from the given statement are true.
The measure of each exterior angle of a regular polygon with sides is . (
A) 5
B) 3
C) 2
D) 4
The measure of each exterior angle of a regular polygon with sides is . (
A) 5
B) 3
C) 2
D) 4

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
79
Expand.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
80
Solve.
In how many distinguishable ways can the letters of the word WINDOW be arranged?
A)120
B)720
C)360
D)36
In how many distinguishable ways can the letters of the word WINDOW be arranged?
A)120
B)720
C)360
D)36

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck


