Exam 8: Sequences, Series, and Combinatorics
Exam 1: Graphs, Functions, and Models189 Questions
Exam 2: More on Functions157 Questions
Exam 3: Quadratic Functions and Equations; Inequalities209 Questions
Exam 4: Polynomial and Rational Functions94 Questions
Exam 5: Exponential and Logarithmic Functions106 Questions
Exam 6: Systems of Equations and Matrices70 Questions
Exam 7: Conic Sections59 Questions
Exam 8: Sequences, Series, and Combinatorics92 Questions
Select questions type
Solve.
-A pendulum bob swings on its first oscillation. On each subsequent oscillation the bob travels of the previous distance. Find the total distance the bob travels before coming to rest.
(Multiple Choice)
4.9/5  (38)
(38)
Find the first 4 terms of the recursively defined sequence.
-
(Multiple Choice)
4.8/5  (35)
(35)
Determine how many of the first 5 statements in the sequence obtainable from the given statement are true.
- is a perfect square.
(Multiple Choice)
4.9/5  (30)
(30)
Solve.
-Suppose 6 cards are drawn from a deck of 52 cards. What is the probability of drawing 3 spades and 3 hearts?
(Multiple Choice)
4.8/5  (36)
(36)
Find the indicated sum.
-Find the sum of the first 13 terms of the geometric sequence:
(Multiple Choice)
4.8/5  (31)
(31)
Solve the problem.
-An experiment was conducted. The results are listed in the following table.
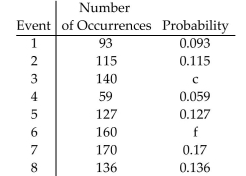 What are the values of c and f?
What are the values of c and f?
(Multiple Choice)
4.9/5  (41)
(41)
Showing 1 - 20 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)