Deck 5: Sequences, Mathematical Induction, and Recursion
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/37
Play
Full screen (f)
Deck 5: Sequences, Mathematical Induction, and Recursion
1
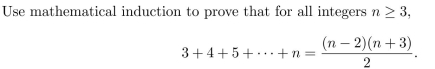


2
Transform the following summation by making the change of variable i = k + 1: 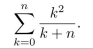
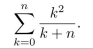
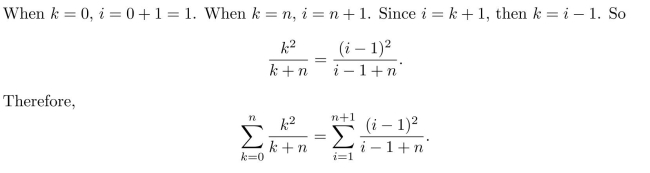
3



4
Use mathematical induction to prove that for all integers 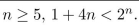
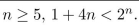

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
5
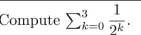

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
6
Use mathematical induction to prove that for all integers 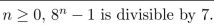
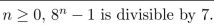

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
7
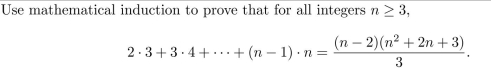

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
8
Use the formula 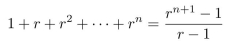
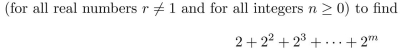
where m is an integer that is at least 1.
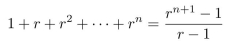
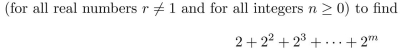
where m is an integer that is at least 1.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
9



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
10
Use strong mathematical induction to prove that for all integers 
either n is prime or n
is a product of prime numbers.

either n is prime or n
is a product of prime numbers.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
11
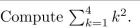

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
12

(a) Is P(0) true? Justify your answer.

(c) Finish the proof started in (b) above.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
13
Use summation notation to rewrite the following: 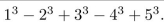
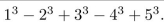

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
14
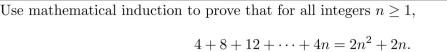

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
15
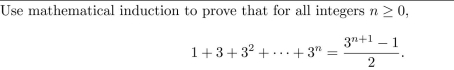

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
16
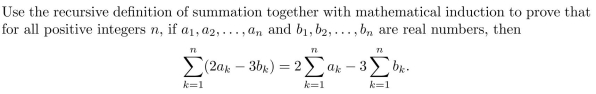

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
17
Use a summation symbol to rewrite the following: 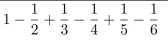
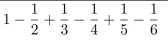

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
18
Use repeated division by 2 to find the binary representation of the number 1032. Show your
work.
work.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
19
Transform the following summation by making the change of variable j = k + 1 : 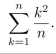
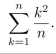

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
20
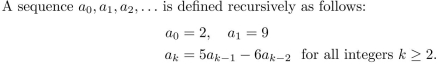
Use strong mathematical induction to prove that for all integers
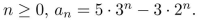

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
21
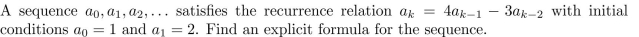

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
22
In a Triple Tower of Hanoi, there are three poles in a row and 3n disks, three of each of n
different sizes, where n is any positive integer. Initially, one of the poles contains all the disks
placed on top of each other in triples of decreasing size. Disks are transferred one by one from
one pole to another, but at no time may a larger disk be placed on top of a smaller disk.
However, a disk may be placed on top of one of the same size. Let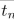
be the minimum number
of moves needed to transfer a tower of 3n disks from one pole to another. Find a recurrence
relation for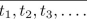
Justify your answer carefully.
different sizes, where n is any positive integer. Initially, one of the poles contains all the disks
placed on top of each other in triples of decreasing size. Disks are transferred one by one from
one pole to another, but at no time may a larger disk be placed on top of a smaller disk.
However, a disk may be placed on top of one of the same size. Let
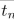
be the minimum number
of moves needed to transfer a tower of 3n disks from one pole to another. Find a recurrence
relation for
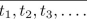
Justify your answer carefully.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
23


Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
24


Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
25
A sequence is defined recursively as follows: 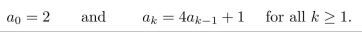
It is proposed that an explicit formula for this sequence is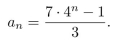
Use mathematical induction to check whether this proposed formula is correct.
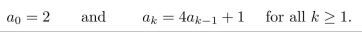
It is proposed that an explicit formula for this sequence is
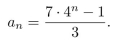
Use mathematical induction to check whether this proposed formula is correct.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
26


Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
27
A sequence 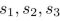
... is defined recursively as follows: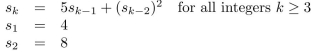
Use (strong) mathematical induction to prove that sn is divisible by 4 for all integers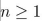
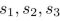
... is defined recursively as follows:
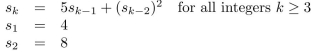
Use (strong) mathematical induction to prove that sn is divisible by 4 for all integers
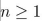

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
28

If appropriate, simplify your answer using one of the following reference formulas:


Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
29
The following while loop is annotated with a pre- and post-condition and also a loop invariant.
Use the loop invariant theorem to prove the correctness of the loop with respect to the pre-
and post-conditions.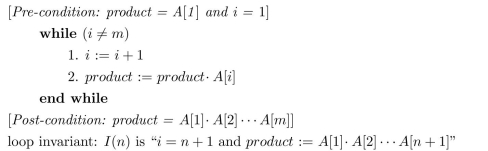
Use the loop invariant theorem to prove the correctness of the loop with respect to the pre-
and post-conditions.
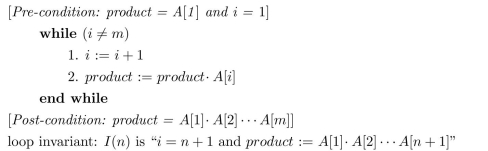

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
30


Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
31


Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
32


Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
33
In a Double Tower of Hanoi with Adjacency Requirement there are three poles in a row and
2n disks, two of each of n different sizes, where n is any positive integer. Initially pole A (at
one end of the row) contains all the disks, placed on top of each other in pairs of decreasing
size. Disks may only be transferred one-by-one from one pole to an adjacent pole and at no
time may a larger disk be placed on top of a smaller one. However a disk may be placed on
top of another one of the same size. Let C be the pole at the other end of the row and let

2n disks, two of each of n different sizes, where n is any positive integer. Initially pole A (at
one end of the row) contains all the disks, placed on top of each other in pairs of decreasing
size. Disks may only be transferred one-by-one from one pole to an adjacent pole and at no
time may a larger disk be placed on top of a smaller one. However a disk may be placed on
top of another one of the same size. Let C be the pole at the other end of the row and let



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
34
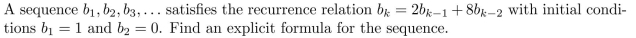

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
35


Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
36
A sequence is defined recursively as follows: 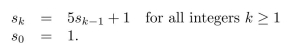
Use mathematical induction to verify that this sequence satisfies the explicit formula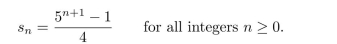
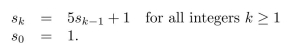
Use mathematical induction to verify that this sequence satisfies the explicit formula
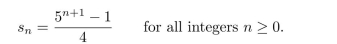

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
37

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck


