Exam 5: Sequences, Mathematical Induction, and Recursion
A sequence satisfies the recurrence relation with initial conditions and . Find an explicit formula for the sequence.
The characteristic equation is . Since , there are two roots: and By the distinct roots theorem, there exist constants and such that
for all integers
Since and , then
Thus for all integers .
Use mathematical induction to prove that for all integers ,
: Let the property be the equation
Note that Show that is true: is true because the left-hand side is and the right-hand side is also.
Show that for all integers , if is true then is true: Let be any integer with , and suppose that
We must show that
Now the left-hand side of is
And the right-hand side of is
Thus the left-hand and right-hand sides of are equal (as was to be shown).
For each integer , let be the equation
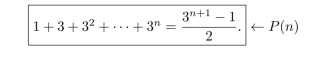 (Recall that by definition )
(a) Is P(0) true? Justify your answer.
(b) In the inductive step of a proof that is true for all integers , we suppose is true (this is the inductive hypothesis), and then we show that is true. Fill in the blanks below to write what we suppose and what we must show for this particular equation.
Proof that for all integers , if is true then is true:
Let be any integer that is greater than or equal to 3 , and suppose that
(Recall that by definition )
(a) Is P(0) true? Justify your answer.
(b) In the inductive step of a proof that is true for all integers , we suppose is true (this is the inductive hypothesis), and then we show that is true. Fill in the blanks below to write what we suppose and what we must show for this particular equation.
Proof that for all integers , if is true then is true:
Let be any integer that is greater than or equal to 3 , and suppose that
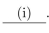 We must showthat
We must showthat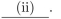 (c) Finish the proof started in (b) above.
(c) Finish the proof started in (b) above.
For each integer , let be the equation![For each integer n \geq 0 , let P ( n ) be the equation (Recall that by definition 1 + 3 + 3 ^ { 2 } + \cdots + 3 ^ { n } = \sum _ { i = 0 } ^ { n } 3 ^ { i } ) (a) P ( 0 ) : \sum _ { i = 0 } ^ { 0 } 3 ^ { i } = \frac { 3 ^ { 0 + 1 } - 1 } { 2 } P ( 0 ) is true because the left-hand side equals \sum _ { i = 0 } ^ { 0 } 3 ^ { i } = 3 ^ { 0 } = 1 , and the right-hand side equals \frac { 3 ^ { 0 + 1 } - 1 } { 2 } = \frac { 3 - 1 } { 2 } = 1 also. (b) P ( k ) : 1 + 3 + 3 ^ { 2 } + \cdots + 3 ^ { k } = \frac { 3 ^ { k + 1 } - 1 } { 2 } P ( k + 1 ) : 1 + 3 + 3 ^ { 2 } + \cdots + 3 ^ { k + 1 } = \frac { 3 ^ { ( k + 1 ) + 1 } - 1 } { 2 } , Or, equivalently, P ( k + 1 ) is 1 + 3 + 3 ^ { 2 } + \cdots + 3 ^ { k + 1 } = \frac { 3 ^ { k + 2 } - 1 } { 2 } . (c) Proof that for all integers k \geq 0 , if P ( k ) is true then P ( k + 1 ) is true: Let k be any integer that is greater than or equal to 0 , and suppose that 1 + 3 + 3 ^ { 2 } + \cdots + 3 ^ { k } = \frac { 3 ^ { k + 1 } - 1 } { 2 } . \quad \leftarrow \quad \begin{array} { l } P ( k ) \\ \text { inductive hypothesis } \end{array} We must show that 1 + 3 + 3 ^ { 2 } + \cdots + 3 ^ { k + 1 } = \frac { 3 ^ { k + 2 } - 1 } { 2 } . \quad \leftarrow P ( k + 1 ) Now the left-hand side of P ( k + 1 ) is 1 + 3 + 3 ^ { 2 } + \cdots + 3 ^ { k + 1 } = 1 + 3 + 3 ^ { 2 } + \cdots + 3 ^ { k } + 3 ^ { k + 1 } by making the next-to-last term explicit = \frac { 3 ^ { k + 1 } - 1 } { 2 } + 3 ^ { k + 1 } = \frac { 3 ^ { k + 1 } - 1 } { 2 } + \frac { 2 \cdot 3 ^ { k + 1 } } { 2 } = \frac { 3 \cdot 3 ^ { k + 1 } - 1 } { 2 } = \frac { 3 ^ { k + 2 } - 1 } { 2 \mathrm { by } \text { adding the fractions and combining like terms } } by a law of exponents, = \frac { 3 ^ { k + 2 } - 1 } { 2 } which equals the right-hand side of P ( k + 1 ) . Thus the left-hand and right-hand sides of P ( k + 1 ) are equal [as was to be shown].](https://storage.examlex.com/TB7212/11eccf7b_84c8_7762_8949_2b738b83e659_TB7212_11.jpg)
(Recall that by definition )
(a)
is true because the left-hand side equals , and the right-hand side equals also.
(b)
Or, equivalently, is .
(c) Proof that for all integers , if is true then is true:
Let be any integer that is greater than or equal to 0 , and suppose that
We must show that
Now the left-hand side of is
by making the next-to-last term explicit
by a law of exponents,
which equals the right-hand side of .
Thus the left-hand and right-hand sides of are equal [as was to be shown].
A sequence ... is defined recursively as follows: =5+ for all integers k\geq3 =4 =8 Use (strong) mathematical induction to prove that sn is divisible by 4 for all integers
A sequence is defined recursively as follows: for all integers
Use mathematical induction to verify that this sequence satisfies the explicit formula
For each integer , let be the equation
(Recall that by definition )
(a) Is true? Justify your answer.
(b) In the inductive step of a proof that is true for all integers , we suppose is true (this is the inductive hypothesis), and then we show that is true. Fill in the blanks below to write what we suppose and what we must show for this particular equation.
Proof that for all integers , if is true then is true:
Let be any integer that is greater than or equal to 3 , and suppose that___ We must show that________
(c) Finish the proof started in (b) above.
A sequence satisfies the recurrence relation with initial conditions and . Find an explicit formula for the sequence.
A sequence satisfies the recurrence relation with initial conditions and . Find an explicit formula for the sequence.
A sequence is defined recursively as follows:
=2,=9 =5-6 for all integers k\geq2
Use strong mathematical induction to prove that for all integers
For each integer , let be the equation
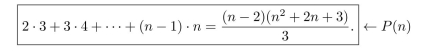 (Recall that by definition
(a) Is true? Justify your answer.
(b) In the inductive step of a proof that is true for all integers , we suppose is true (this is the inductive hypothesis), and then we show that is true. Fill in the blanks below to write what we suppose and what we must show for this particular equation.
Proof that for all integers , if is true then is true:
Let be any integer that is greater than or equal to 3 , and suppose that____ We must show that_____
(c) Finish the proof started in (b) above.
(Recall that by definition
(a) Is true? Justify your answer.
(b) In the inductive step of a proof that is true for all integers , we suppose is true (this is the inductive hypothesis), and then we show that is true. Fill in the blanks below to write what we suppose and what we must show for this particular equation.
Proof that for all integers , if is true then is true:
Let be any integer that is greater than or equal to 3 , and suppose that____ We must show that_____
(c) Finish the proof started in (b) above.
A sequence is defined as follows:
(a) Find and .
(b) Simplify the expression
using one of the following reference formulas:
for all integers .
for all integers and all real numbers .
(c) Use iteration to guess an explicit formula for the sequence
Transform the following summation by making the change of variable j = k + 1 :
A sequence is defined as follows:
(a) Find , and .
(b) Supposing that , find a similar numerical expression for by substituting the right-hand side of this equation in place of in the equation
(c) Guess an explicit formula for . Simplify your answer using one of the following reference formulas:
for all integers .
for all integers and all real numbers .
Define a set recursively as follows:
I. BASIS:
II. RECURSION: If and are in , then
a. 0s\inS b. s0\inS c. 1s1t\inS d. s1t1\inS
III. RESTRICTION: No strings other than those derived from I and II are in . Use structural induction to prove that every string in contains an even number of l's.
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)