Deck 10: Graphs and Trees
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/14
Play
Full screen (f)
Deck 10: Graphs and Trees
1
Draw a directed graph with the following adjacency matrix: 

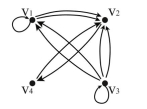
2
A certain graph has 19 vertices, 16 edges, and no circuits. Is it connected? Explain.
No. The graph is not connected because if it were connected, then, since it is circuit-free, it
would be a tree and would have 18 edges instead of 19 edges.
would be a tree and would have 18 edges instead of 19 edges.
3
a. Prove that having n vertices, where n is a positive integer, is an invariant for graph
isomorphism.b. Prove that having a vertex of degree 3 is an invariant for graph isomorphism.
isomorphism.b. Prove that having a vertex of degree 3 is an invariant for graph isomorphism.
 Note: An alternative proof for this problem could consider two cases separately. In one case
Note: An alternative proof for this problem could consider two cases separately. In one casethe vertex v0 in G of degree 3 would have three distinct edges incident on it, and in the other
case there would be one edge and one loop incident on it.
4
Determine whether each of the following graphs has an Euler circuit. If it does have an Euler
circuit, find such a circuit. If it does not have an Euler circuit, explain why you can be 100%
sure that it does not.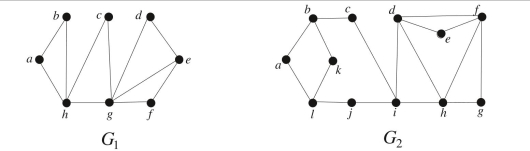
circuit, find such a circuit. If it does not have an Euler circuit, explain why you can be 100%
sure that it does not.


Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
5
Find the following matrix product: 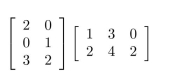
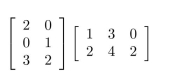

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
6
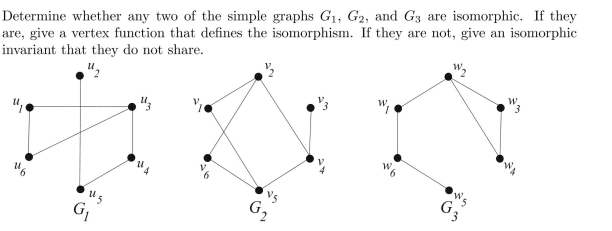

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
7
For each of (a)-(c) below, either draw a graph with the specified properties or else explain why
no such graph exists.
(a) Graph with six vertices of degrees 1, 1, 2, 2, 2, and 3.
(b) Graph with four vertices of degrees 1, 2, 2, and 5.
(c) Simple graph with four vertices of degrees 1, 1, 1, and 5.
no such graph exists.
(a) Graph with six vertices of degrees 1, 1, 2, 2, 2, and 3.
(b) Graph with four vertices of degrees 1, 2, 2, and 5.
(c) Simple graph with four vertices of degrees 1, 1, 1, and 5.

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
8
Either draw a graph with the given specification or explain why no such graph exists.
(a) full binary tree with 16 vertices of which 6 are internal vertices
(b) binary tree, height 3, 9 vertices
(c) binary tree, height 4, 18 terminal vertices
(a) full binary tree with 16 vertices of which 6 are internal vertices
(b) binary tree, height 3, 9 vertices
(c) binary tree, height 4, 18 terminal vertices

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
9
Consider the adjacency matrix for a graph that is shown below. Answer the following questions
by examining the matrix and its powers only, not by drawing the graph. Show your work in a
way that makes your reasoning clear.

by examining the matrix and its powers only, not by drawing the graph. Show your work in a
way that makes your reasoning clear.



Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
10
Determine whether each of the following graphs has a Hamiltonian circuit. If it does have an
Hamiltonian circuit, find such a circuit. If it does not have an Hamiltonian circuit, explain
why you can be 100% sure that it does not.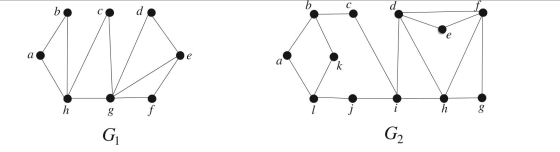
Hamiltonian circuit, find such a circuit. If it does not have an Hamiltonian circuit, explain
why you can be 100% sure that it does not.


Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
11
A certain connected graph has 68 vertices and 72 edges. Does it have a circuit? Explain.

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
12
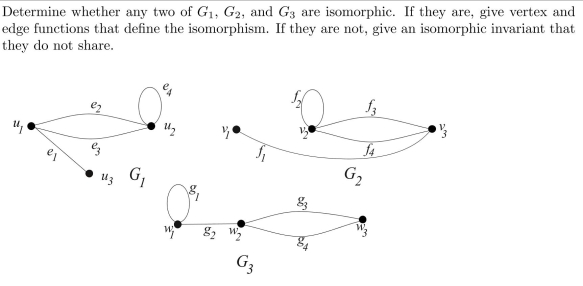

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
13
If a graph has vertices of degrees 1, 1, 2, 3, and 3, how many edges does it have? Why?

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
14
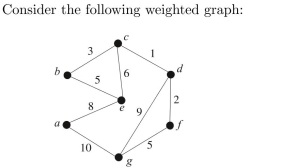
(a) Use Kruskal's algorithm to find a minimum spanning tree for the graph, and indicate the
order in which edges are added to form the tree.
(b) Use Prim's algorithm starting with vertex a to find a minimum spanning tree for the
graph, and indicate the order in which edges are added to form the tree.
(c) Use Dijkstra's algorithm to find the shortest path from a to

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck


