Exam 10: Graphs and Trees
Exam 1: Speaking Mathematically13 Questions
Exam 2: The Logic of Compound Statements27 Questions
Exam 3: The Logic of Quantified Statements16 Questions
Exam 4: Elementary Number Theory and Methods of Proof28 Questions
Exam 5: Sequences, Mathematical Induction, and Recursion37 Questions
Exam 6: Set Theory19 Questions
Exam 7: Functions21 Questions
Exam 8: Relations19 Questions
Exam 9: Counting and Probability25 Questions
Exam 10: Graphs and Trees14 Questions
Exam 11: Analyzing Algorithm Efficiency22 Questions
Exam 12: Regular Expressions and Finite State Automata14 Questions
Select questions type
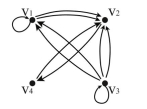
Draw a directed graph with the following adjacency matrix: 
Free
(Essay)
4.7/5  (39)
(39)
Correct Answer:
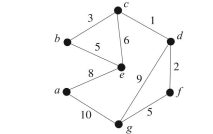 (a) Use Kruskal's algorithm to find a minimum spanning tree for the graph, and indicate the
order in which edges are added to form the tree.
(b) Use Prim's algorithm starting with vertex a to find a minimum spanning tree for the
graph, and indicate the order in which edges are added to form the tree.
(c) Use Dijkstra's algorithm to find the shortest path from a to
(a) Use Kruskal's algorithm to find a minimum spanning tree for the graph, and indicate the
order in which edges are added to form the tree.
(b) Use Prim's algorithm starting with vertex a to find a minimum spanning tree for the
graph, and indicate the order in which edges are added to form the tree.
(c) Use Dijkstra's algorithm to find the shortest path from a to
Free
(Essay)
4.8/5  (32)
(32)
Correct Answer:
a. Order of adding the edges: or
b. Order of adding the edges:
c. Dijkstra's algorithm shows that the shortest path from to has length 15 . Because , and , we can work backward to find that the path is . 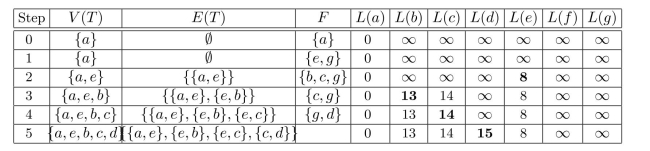
Determine whether each of the following graphs has an Euler circuit. If it does have an Euler circuit, find such a circuit. If it does not have an Euler circuit, explain why you can be 100% sure that it does not. 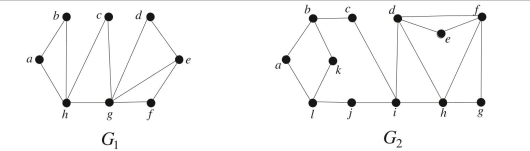
Free
(Essay)
4.8/5  (44)
(44)
Correct Answer:
(the left-hand graph) does not have an Euler circuit because it has a vertex of odd degree. In fact both vertices and have odd degree.
(the right-hand graph) does not have an Euler circuit because it has a vertex of odd degree. In fact both vertices and have odd degree.
Determine whether each of the following graphs has a Hamiltonian circuit. If it does have an Hamiltonian circuit, find such a circuit. If it does not have an Hamiltonian circuit, explain why you can be 100% sure that it does not. 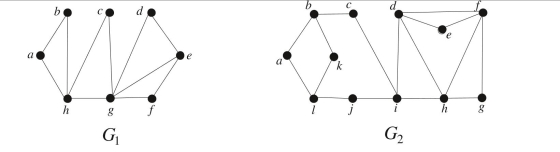
(Essay)
4.7/5  (36)
(36)
a. Prove that having n vertices, where n is a positive integer, is an invariant for graph
isomorphism.
b. Prove that having a vertex of degree 3 is an invariant for graph isomorphism.
(Essay)
4.9/5  (28)
(28)
A certain connected graph has 68 vertices and 72 edges. Does it have a circuit? Explain.
(Essay)
4.8/5  (34)
(34)
Consider the adjacency matrix for a graph that is shown below. Answer the following questions by examining the matrix and its powers only, not by drawing the graph. Show your work in a way that makes your reasoning clear.  (a) How many walks of length 2 are there from to ?
(b) How many walks of length 2 are there from to ?
(c) How many walks of length 2 are there from to ?
(a) How many walks of length 2 are there from to ?
(b) How many walks of length 2 are there from to ?
(c) How many walks of length 2 are there from to ?
(Essay)
4.7/5  (31)
(31)
Either draw a graph with the given specification or explain why no such graph exists.
(a) full binary tree with 16 vertices of which 6 are internal vertices
(b) binary tree, height 3, 9 vertices
(c) binary tree, height 4, 18 terminal vertices
(Essay)
4.8/5  (38)
(38)
A certain graph has 19 vertices, 16 edges, and no circuits. Is it connected? Explain.
(Essay)
4.8/5  (28)
(28)
For each of (a)-(c) below, either draw a graph with the specified properties or else explain why no such graph exists.
(a) Graph with six vertices of degrees 1, 1, 2, 2, 2, and 3.
(b) Graph with four vertices of degrees 1, 2, 2, and 5.
(c) Simple graph with four vertices of degrees 1, 1, 1, and 5.
(Essay)
4.8/5  (35)
(35)
Determine whether any two of , and are isomorphic. If they are, give vertex and edge functions that define the isomorphism. If they are not, give an isomorphic invariant that they do not share.
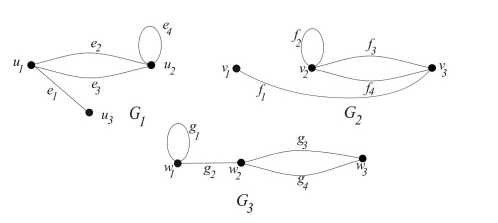
(Essay)
4.7/5  (38)
(38)
If a graph has vertices of degrees 1, 1, 2, 3, and 3, how many edges does it have? Why?
(Essay)
4.7/5  (33)
(33)
Determine whether any two of the simple graphs , and are isomorphic. If they are, give a vertex function that defines the isomorphism. If they are not, give an isomorphic invariant that they do not share.
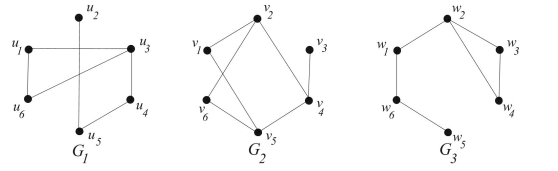
(Essay)
5.0/5  (23)
(23)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)