Deck 7: Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/21
Play
Full screen (f)
Deck 7: Functions
1
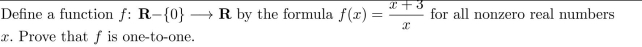
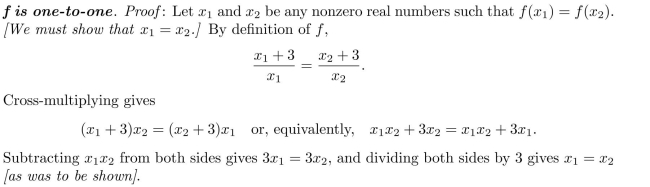
2


3

a. Proof that g is one-to-one: Suppose x1 and x2 are any nonzero real numbers and
g(x1) = g(x2). [We must show that x1 = x2.]
By definition of g,
![a. Proof that g is one-to-one: Suppose x1 and x2 are any nonzero real numbers and g(x1) = g(x2). [We must show that x1 = x2.] By definition of g, Proof that g is onto: Let y be any nonzero real number. [We must show that there is a nonzero real number whose image under g is y.]](https://storage.examlex.com/TB7212/11eb4916_5842_4c72_b114_c99bb3753757_TB7212_00.jpg) Proof that g is onto: Let y be any nonzero real number. [We must show that there is a
Proof that g is onto: Let y be any nonzero real number. [We must show that there is a
nonzero real number whose image under g is y.]
g(x1) = g(x2). [We must show that x1 = x2.]
By definition of g,
![a. Proof that g is one-to-one: Suppose x1 and x2 are any nonzero real numbers and g(x1) = g(x2). [We must show that x1 = x2.] By definition of g, Proof that g is onto: Let y be any nonzero real number. [We must show that there is a nonzero real number whose image under g is y.]](https://storage.examlex.com/TB7212/11eb4916_5842_4c72_b114_c99bb3753757_TB7212_00.jpg) Proof that g is onto: Let y be any nonzero real number. [We must show that there is a
Proof that g is onto: Let y be any nonzero real number. [We must show that there is anonzero real number whose image under g is y.]
4
Let f be a function from a set X to a set Y. Define precisely (but concisely) what it means for
f to be onto.
f to be onto.

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
5
Fill in the blanks: 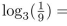
because .
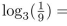
because .

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
6
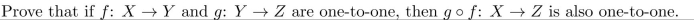

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
7


Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
8
Is 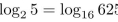
Why or why not?
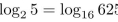
Why or why not?

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
9


Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
10


Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
11
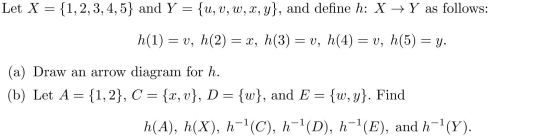

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
12


Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
13
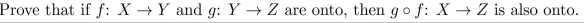

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
14
(a) Draw an arrow diagram for a function that is onto but not one-to-one.
(b) Draw an arrow diagram for a function that is one-to-one but not onto.
(b) Draw an arrow diagram for a function that is one-to-one but not onto.

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
15
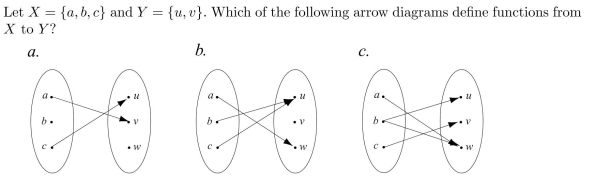
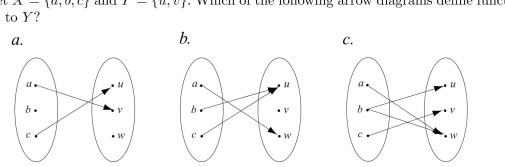

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
16


Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
17
Let f be a function from a set X to a set Y. Define precisely (but concisely) what it means for
f to be one-to-one.
f to be one-to-one.

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
18


Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
19
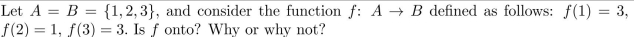

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
20
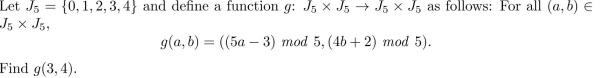

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck
21
Prove that the set of all integers and the set of all odd integers have the same cardinality.

Unlock Deck
Unlock for access to all 21 flashcards in this deck.
Unlock Deck
k this deck


