Exam 7: Functions
Is Why or why not?
The two quantities are equal. Let . Then, by definition of logarithm, . Now
So
Raising both sides to the power gives that
Hence, by definition of logarithm,
Since both quantities equal ,
Let f be a function from a set X to a set Y. Define precisely (but concisely) what it means for f to be one-to-one.
Sample correct answers: A function from a set to a set is one-to-one if, and only if, given any elements and in , if then .
A function from a set to a set is one-to-one if, and only if, given any elements and in , if then .
A function from a set to a set is one-to-one if, and only if, given any element in , there is at most one element in such that .
A function from a set to a set is one-to-one if, and only if, each element in , is the image of at most one element in .
Let be the set of all even integers, and define a function as follows:
(a) Prove that is one-to-one and onto
(b) Find a formula for the inverse function .
(c) Does the set of all even integers have the same cardinality as the set of all integers? Why or why not?
a. Proof that is one-to-one: Suppose and are in and WWe must show that By definition of . Dividing both sides by 2 gives [as was to be shown].
Proof that is onto: Let be any even integer. [We must show that there is an integer whose image under is m.]
Let . Then is an integer because is even, and
[as was to be shown].
Conclusion: Since is both one-to-one and onto, is a one-to-one correspondence.
b. Given any even integer .
c. The set of all even integers has the same cardinality as the set of all integers because there is a one-to-one correspondence from the set of all integers to the set of all even integers.
Define a function as follows: for all real numbers ,
Then is both one-to-one and onto. Find the inverse function .
Define as follows: for all in .
(a) ?
(b) Is one-to-one? Prove or give a counterexample.
(c) Is onto? Prove or give a counterexample.
(d) Is a one-to-one correspondence? If not, explain why not.
If yes, find .
Let be the set of all nonzero real numbers. Define a function from to by the formula , for all nonzero real numbers .
(a) Show that is a one-to-one correspondence from to .
(b) Find .
Let be the set of all strings in 0's and 1's, and define a function as follows: for all strings in ,
(a) What is ? ? ?
(b) Is one-to-one? Prove or give a counterexample.
(c) Is onto? Prove or give a counterexample.
(d) Is a one-to-one correspondence? If so, find .
(a) Draw an arrow diagram for a function that is onto but not one-to-one.
(b) Draw an arrow diagram for a function that is one-to-one but not onto.
Let , and consider the function defined as follows: , . Is onto? Why or why not?
Let and , and define as follows:
(a) Draw an arrow diagram for .
(b) Let , and . Find
Prove that the set of all integers and the set of all odd integers have the same cardinality.
Is the set of all squares of positive integers countable? That is, is the set for some positive integer a countable set. Justify your answer.
Let be the set of all strings in 0's and 1's, and define a function : as follows: for each string in ,
the number of 1's in minus the number of 0 's in
(a) What is ?
(b) Is one-to-one? Prove or give a counterexample.
(c) Is onto? Prove or give a counterexample.
Let be the set of all strings in 0 's and 1's, and define a function as follows: for each string in ,
(a) What is ? ?
(b) Is one-to-one? Prove or give a counterexample.
(c) Is onto? Prove or give a counterexample.
Let f be a function from a set X to a set Y. Define precisely (but concisely) what it means for f to be onto.
Let and . Which of the following arrow diagrams define functions from to ?
a.
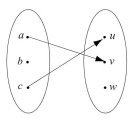 b.
b.
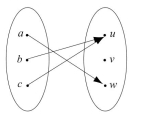 c.
c.
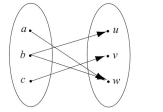
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)