Deck 8: Relations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/19
Play
Full screen (f)
Deck 8: Relations
1
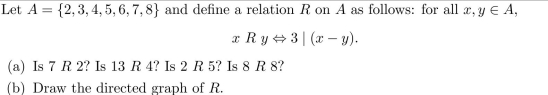
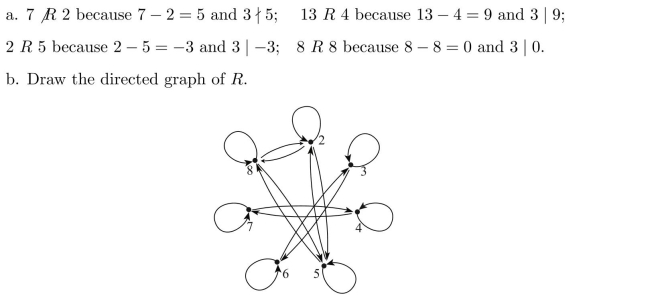
2
An RSA cipher has public key pq = 65 and e = 7.
(a) Translate the message YES into its numeric equivalent, and use the formula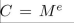
(mod pq) to encrypt the message.
(b) Decrypt the ciphertext 50 16 and translate the result into letters of the alphabet to
discover the message.
(a) Translate the message YES into its numeric equivalent, and use the formula
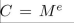
(mod pq) to encrypt the message.
(b) Decrypt the ciphertext 50 16 and translate the result into letters of the alphabet to
discover the message.

3
Find a positive inverse for 7 modulo 48. (That is, find a positive integer n such that 7n ≡ 1
(mod 48).)
(mod 48).)
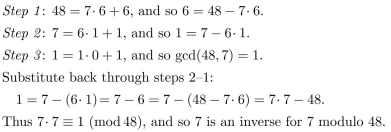
4


Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
5
Let S be the set of all strings of 0's and 1's of length 3. Define a relation R on S as follows:
for all strings s and t in S,
(a) Prove that R is an equivalence relation on S.
(b) Find the distinct equivalence classes of R.
for all strings s and t in S,

(a) Prove that R is an equivalence relation on S.
(b) Find the distinct equivalence classes of R.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
6
Let R be the relation defined on the set of all integers Z as follows: for all integers m and n, 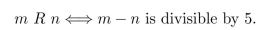
(a) Is R reflexive? Prove or give a counterexample.
(b) Is R symmetric? Prove or give a counterexample.
(c) Is R transitive? Prove or give a counterexample.
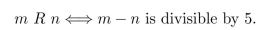
(a) Is R reflexive? Prove or give a counterexample.
(b) Is R symmetric? Prove or give a counterexample.
(c) Is R transitive? Prove or give a counterexample.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
7
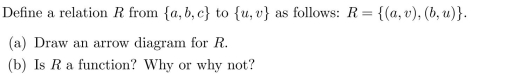

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
8
Define a relation S on the set of positive integers as follows: for all positive integers m and n, 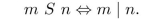
(a) Is S reflexive? Justify your answer.
(b) Is S symmetric? Justify your answer.
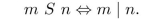
(a) Is S reflexive? Justify your answer.
(b) Is S symmetric? Justify your answer.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
9
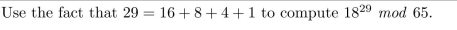

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
10


Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
11
Let A = {1, 2, 3, 4}. The following relation R is an equivalence relation on A:
R = {(1, 1), (1, 3), (1, 4), (2, 2), (3, 1), (3, 3), (3, 4), (4, 1), (4, 3), (4, 4)}.
(a) Draw the directed graph of R.
(b) Find the distinct equivalence classes of R.
R = {(1, 1), (1, 3), (1, 4), (2, 2), (3, 1), (3, 3), (3, 4), (4, 1), (4, 3), (4, 4)}.
(a) Draw the directed graph of R.
(b) Find the distinct equivalence classes of R.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
12
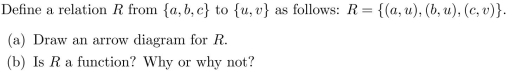

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
13
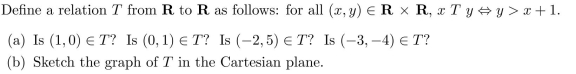

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
14
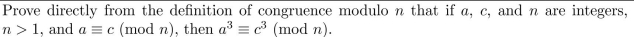

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
15
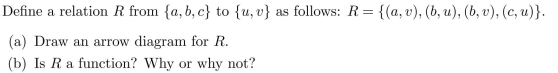

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
16


Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
17
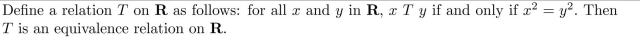
(a) Prove that T is an equivalence relation on R.
(b) Find the distinct equivalence classes of T.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
18
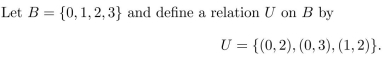
Is U transitive? Justify your answer.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
19
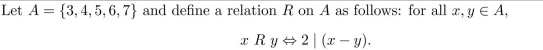
(a) Is 6 R 3? Is 4 R 6?
(b) Draw the directed graph of R.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck


