Exam 8: Relations
Exam 1: Speaking Mathematically13 Questions
Exam 2: The Logic of Compound Statements27 Questions
Exam 3: The Logic of Quantified Statements16 Questions
Exam 4: Elementary Number Theory and Methods of Proof28 Questions
Exam 5: Sequences, Mathematical Induction, and Recursion37 Questions
Exam 6: Set Theory19 Questions
Exam 7: Functions21 Questions
Exam 8: Relations19 Questions
Exam 9: Counting and Probability25 Questions
Exam 10: Graphs and Trees14 Questions
Exam 11: Analyzing Algorithm Efficiency22 Questions
Exam 12: Regular Expressions and Finite State Automata14 Questions
Select questions type
Let and define a relation on as follows: for all ,
(a) Is ? Is ? Is ? Is ?
(b) Draw the directed graph of .
Free
(Essay)
5.0/5  (39)
(39)
Correct Answer:
a. because and because and ;
because and because and .
b. Draw the directed graph of .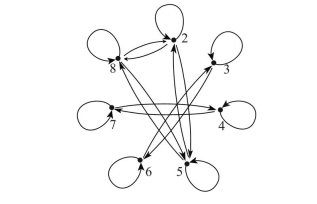
Let and define a relation on as follows: .
(a) Draw the directed graph of .
(b) Is reflexive? Explain.
(c) Is symmetric? Explain.
(d) Is transitive? Explain.
Free
(Essay)
4.7/5  (34)
(34)
Correct Answer:
a. 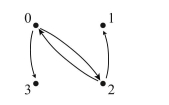 b. is not reflexive because, for example, .
b. is not reflexive because, for example, .
c. is not symmetric because, for example, but .
d. is not transitive because, for example, and but .
Define a relation from to as follows: .
(a) Draw an arrow diagram for .
(b) Is a function? Why or why not?
(Essay)
4.8/5  (31)
(31)
An RSA cipher has public key pq = 65 and e = 7.
(a) Translate the message YES into its numeric equivalent, and use the formula (mod pq) to encrypt the message.
(b) Decrypt the ciphertext 50 16 and translate the result into letters of the alphabet to discover the message.
(Essay)
4.9/5  (32)
(32)
Define a relation from to as follows: .
(a) Draw an arrow diagram for .
(b) Is a function? Why or why not?
(Essay)
4.8/5  (33)
(33)
Define a relation S on the set of positive integers as follows: for all positive integers m and n,
(a) Is S reflexive? Justify your answer.
(b) Is S symmetric? Justify your answer.
(Essay)
4.8/5  (29)
(29)
Let and define a relation on as follows: for all ,
(a) Is 6 R 3? Is 4 R 6?
(b) Draw the directed graph of R.
(Essay)
4.8/5  (41)
(41)
Let R be the relation defined on the set of all integers Z as follows: for all integers m and n,
(a) Is R reflexive? Prove or give a counterexample.
(b) Is R symmetric? Prove or give a counterexample.
(c) Is R transitive? Prove or give a counterexample.
(Essay)
5.0/5  (39)
(39)
Define a relation on as follows: for all and in if and only if . Then is an equivalence relation on .
(a) Prove that T is an equivalence relation on R.
(b) Find the distinct equivalence classes of T.
(Essay)
4.9/5  (39)
(39)
Let and define a relation on by
Is U transitive? Justify your answer.
(Essay)
5.0/5  (35)
(35)
Find a positive inverse for 7 modulo 48. (That is, find a positive integer n such that 7n ≡ 1 (mod 48).
(Essay)
4.7/5  (35)
(35)
Define a relation on the set as follows:
(a) Is symmetric? Justify your answer.
(b) Is transitive? Justify your answer.
(Essay)
4.9/5  (37)
(37)
Let A = {1, 2, 3, 4}. The following relation R is an equivalence relation on A:
R = {(1, 1), (1, 3), (1, 4), (2, 2), (3, 1), (3, 3), (3, 4), (4, 1), (4, 3), (4, 4)}.
(a) Draw the directed graph of R.
(b) Find the distinct equivalence classes of R.
(Essay)
5.0/5  (21)
(21)
Prove directly from the definition of congruence modulo that if , and are integers, , and , then .
(Essay)
4.8/5  (31)
(31)
Let S be the set of all strings of 0's and 1's of length 3. Define a relation R on S as follows: for all strings s and t in S,
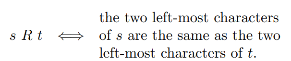 (a) Prove that R is an equivalence relation on S.
(b) Find the distinct equivalence classes of R.
(a) Prove that R is an equivalence relation on S.
(b) Find the distinct equivalence classes of R.
(Essay)
4.9/5  (32)
(32)
Define a relation from to as follows: .
(a) Draw an arrow diagram for .
(b) Is a function? Why or why not?
(Essay)
4.9/5  (28)
(28)
Define a relation from to as follows: for all .
(a) Is Is Is Is
(b) Sketch the graph of in the Cartesian plane.
(Essay)
4.9/5  (35)
(35)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)