Deck 10: Graphs
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/14
Play
Full screen (f)
Deck 10: Graphs
1
What is the chromatic number of each of the graphs in problem 1? Explain your answers.

2
Is the following graph bipartite? Justify your answer. 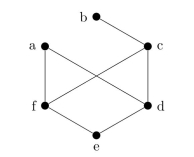

The graph is bipartite. The vertex set can be partitioned into {a, c, e} and {b, d, f}. There are no edges connecting a vertex in one set and a vertex in the other set.
3
Consider the graphs 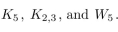 Which of these graphs have an Euler circuit? Which have an Euler path?
Which of these graphs have an Euler circuit? Which have an Euler path?
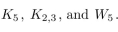 Which of these graphs have an Euler circuit? Which have an Euler path?
Which of these graphs have an Euler circuit? Which have an Euler path?K5 has five vertices each of degree 4, so it has an Euler circuit (and an Euler path) since all its vertices have even degree. K2,3 has two vertices of degree 3 and three vertices of degree 2, so it does not have an Euler circuit, but it does have an Euler path since it has exactly two vertices of odd degree. W5 has five vertices of degree 3 and one vertex of degree 5, so it has neither an Euler circuit nor an Euler path since it has more than two vertices of odd degree.
4
How many vertices and how many edges do each of the following graphs have? 
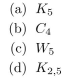

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
5
Does a simple graph that has five vertices each of degree 3 exist? If so, draw such a graph. If not, explain why no such graph exists.

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
6
Use Dijkstra's algorithm to find the length of the shortest path between the vertices a and z in the following

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
7
Is there an Euler circuit in the following graph? If so, find such a circuit. If not, explain why no such circuit exists. 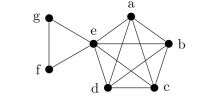


Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
8
Is there a Hamilton circuit in the graph shown in problem 4? If so, find such a circuit. If not, prove why no such circuit exists.

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
9
For each of the following sequences determine whether there is a simple graph whose vertices have these degrees. Draw such a graph if it exists. (a) 0, 1, 1, 2 (b) 2, 2, 2, 2 (c) 1, 2, 3, 4, 5

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
10
How many nonisomorphic simple graphs are there with three vertices? Draw examples of each of these.

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
11
What is the chromatic number of each of the graphs in problem 4?

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
12
Decide whether the graphs G and H are isomorphic. Prove that your answer is correct. 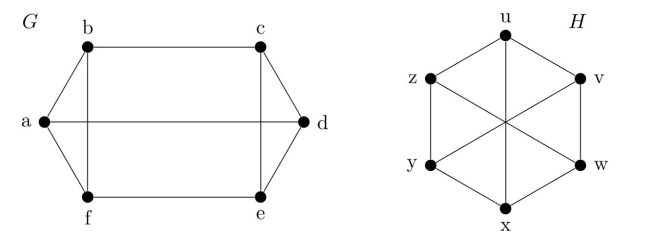


Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
13
Which of the graphs in problem 4 are planar?

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
14
Is the following graph planar? If so draw it without any edges crossing. If it is not, prove that it is not planar. 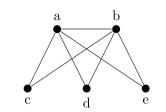


Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck


