Exam 10: Graphs
Which of the graphs in problem 4 are planar?
is nonplanar. is planar, as can easily be seen by drawing it with no crossings, or since it has no subgraph homeomorphic to or is planar as is seen from the usual way of drawing it.
Use Dijkstra's algorithm to find the length of the shortest path between the vertices a and z in the following
First iteration: distinguished vertices: ; labels: . Second iteration: distinguished vertices: labels: . Third iteration: distinguished vertices: labels: . Fourth iteration: distinguished vertices: labels: . Fifth iteration: distinguished vertices: labels: . Since at the next iteration is a distinguished vertex, we conclude that the shortest path has length 13 .
Is the following graph bipartite? Justify your answer. 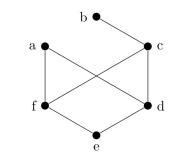
The graph is bipartite. The vertex set can be partitioned into {a, c, e} and {b, d, f}. There are no edges connecting a vertex in one set and a vertex in the other set.
Is there a Hamilton circuit in the graph shown in problem 4? If so, find such a circuit. If not, prove why no such circuit exists.
Does a simple graph that has five vertices each of degree 3 exist? If so, draw such a graph. If not, explain why no such graph exists.
What is the chromatic number of each of the graphs in problem 1? Explain your answers.
How many nonisomorphic simple graphs are there with three vertices? Draw examples of each of these.
Consider the graphs Which of these graphs have an Euler circuit? Which have an Euler path?
Decide whether the graphs G and H are isomorphic. Prove that your answer is correct. 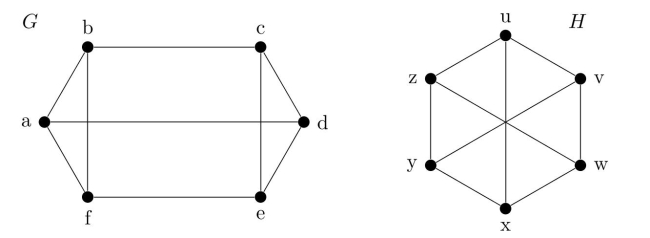
Is there an Euler circuit in the following graph? If so, find such a circuit. If not, explain why no such circuit exists. 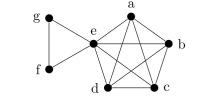
How many vertices and how many edges do each of the following graphs have? (a)
(b)
(c)
(d)
For each of the following sequences determine whether there is a simple graph whose vertices have these degrees. Draw such a graph if it exists. (a) 0, 1, 1, 2 (b) 2, 2, 2, 2 (c) 1, 2, 3, 4, 5
Is the following graph planar? If so draw it without any edges crossing. If it is not, prove that it is not planar. 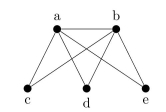
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)