Deck 5: A: Induction and Recursion
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/51
Play
Full screen (f)
Deck 5: A: Induction and Recursion
1
Suppose you wish to use mathematical induction to prove that: 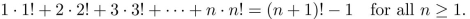 (a) Write P(1). (b) Write P(5). (c) Write P(k). (d) Write P(k + 1). (e) Use mathematical induction to prove that P(n) is true for all n ≥ 1.
(a) Write P(1). (b) Write P(5). (c) Write P(k). (d) Write P(k + 1). (e) Use mathematical induction to prove that P(n) is true for all n ≥ 1.
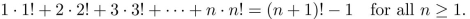 (a) Write P(1). (b) Write P(5). (c) Write P(k). (d) Write P(k + 1). (e) Use mathematical induction to prove that P(n) is true for all n ≥ 1.
(a) Write P(1). (b) Write P(5). (c) Write P(k). (d) Write P(k + 1). (e) Use mathematical induction to prove that P(n) is true for all n ≥ 1.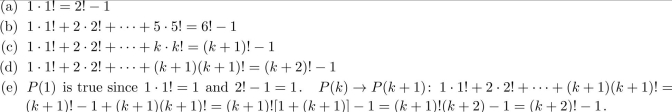
2
Use mathematical induction to prove that every integer amount of postage of six cents or more can be formed using 3-cent and 4-cent stamps.
P(6): Six cents postage can be made from two 3-cent stamps. P(k) → P(k + 1): either replace a 3-cent stamp by a 4-cent stamp or else (if there are only 4-cent stamps in the pile of stamps making k cents postage) replace two 4-cent stamps by three 3-cent stamps.
3
Use mathematical induction to prove that 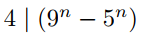 for all
for all 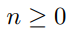
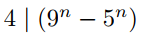 for all
for all 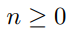
P(0): 4 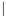 1-1 is true since 4
1-1 is true since 4 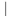 0 . https://storage.examlex.com/TB34225555/
0 . https://storage.examlex.com/TB34225555/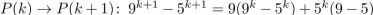 . each term is divisible by
. each term is divisible by 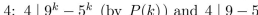
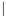 1-1 is true since 4
1-1 is true since 4 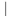 0 . https://storage.examlex.com/TB34225555/
0 . https://storage.examlex.com/TB34225555/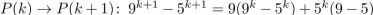 . each term is divisible by
. each term is divisible by 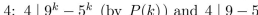
4
Use mathematical induction to prove that any integer amount of postage from 18 cents on up can be made from an infinite supply of 4-cent and 7-cent stamps.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
5
Use mathematical induction to prove that 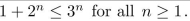
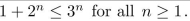

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
6
Let 


Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
7
Use mathematical induction to show that n lines in the plane passing through the same point divide the plane into 2n regions.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
8
Use mathematical induction to prove that 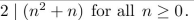
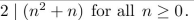

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
9
Use mathematical induction to prove that 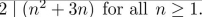
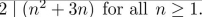

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
10
Use mathematical induction to prove that 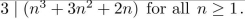
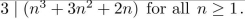

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
11
Use mathematical induction to prove that 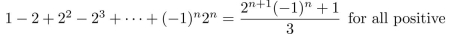 integers n.
integers n.
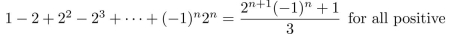 integers n.
integers n.
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
12
Use mathematical induction to prove that 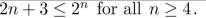
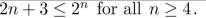

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
13
Use mathematical induction to prove that 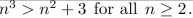
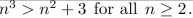

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
14
Use mathematical induction to prove that 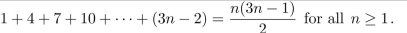
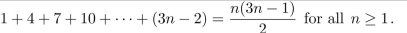

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose you wish to prove that the following is true for all positive integers n by using mathematical induction:
1+3+5+...+(2 n-1)=n2
(a) Write P(1).
(b) Write P(72).
(c) Write P(73).
(d) Use P(72) to prove P(73).
(e) Write P(k).
(f) Write P(k + 1).
(g) Use mathematical induction to prove that P(n) is true for all positive integers n.
1+3+5+...+(2 n-1)=n2
(a) Write P(1).
(b) Write P(72).
(c) Write P(73).
(d) Use P(72) to prove P(73).
(e) Write P(k).
(f) Write P(k + 1).
(g) Use mathematical induction to prove that P(n) is true for all positive integers n.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
16
Suppose that the only paper money consists of 3-dollar bills and 10-dollar bills. Show that any dollar amount greater than 17 dollars could be made from a combination of these bills.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
17
A T -omino is a tile pictured at the right. Prove that every 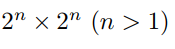 chessboard can be tiled with T-ominoes.
chessboard can be tiled with T-ominoes.
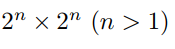 chessboard can be tiled with T-ominoes.
chessboard can be tiled with T-ominoes. 
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
18
Prove that 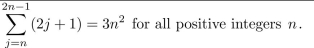
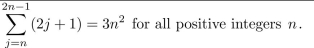

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
19
Use mathematical induction to prove that 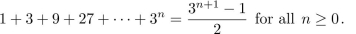
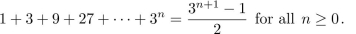

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
20
Floor borders one foot wide and of varying lengths are to be covered with nonoverlapping tiles that are available in two sizes: 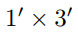 and
and  sizes. Assuming that the supply of each size is infinite, prove that every
sizes. Assuming that the supply of each size is infinite, prove that every 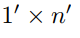 border
border 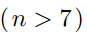 can be covered with these tiles.
can be covered with these tiles.
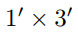 and
and  sizes. Assuming that the supply of each size is infinite, prove that every
sizes. Assuming that the supply of each size is infinite, prove that every 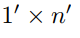 border
border 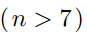 can be covered with these tiles.
can be covered with these tiles.
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
21
give a recursive definition (with initial condition(s)) of 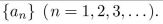
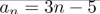
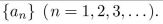
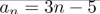

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
22
give a recursive definition with initial condition(s).
The set {1, 5, 9, 13, 17, . . .}
The set {1, 5, 9, 13, 17, . . .}

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
23
Prove that 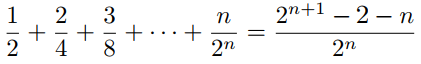 for all https://storage.examlex.com/TB6843/
for all https://storage.examlex.com/TB6843/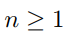 .
.
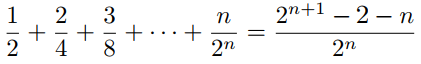 for all https://storage.examlex.com/TB6843/
for all https://storage.examlex.com/TB6843/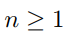 .
.
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
24
Prove that the distributive law 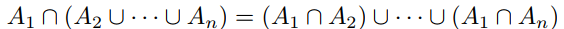 is true for all
is true for all 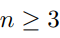
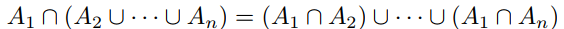 is true for all
is true for all 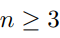

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
25
Use mathematical induction to prove that 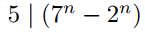 for all
for all 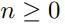
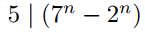 for all
for all 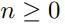

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
26
give a recursive definition (with initial condition(s)) of 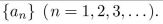
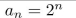
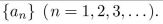
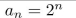

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
27
give a recursive definition (with initial condition(s)) of 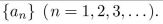
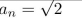
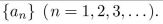
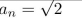

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
28
give a recursive definition with initial condition(s).
The function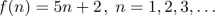
The function
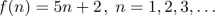

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
29
give a recursive definition (with initial condition(s)) of 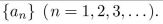
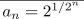
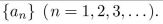
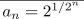

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
30
give a recursive definition with initial condition(s).
The sequence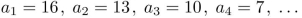
The sequence
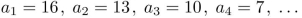

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
31
Find the error in the following proof of this "theorem":
"Theorem: Every positive integer equals the next largest positive integer."
"Proof: Let P(n) be the proposition ' n=n+1 .' To show that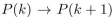
true for some k , so that k=k+1 . Add 1 to both sides of this equation to obtain k+1=k+2 , which is
P(k+1) . Therefore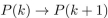
is true. Hence P(n) is true for all positive integers n ."
"Theorem: Every positive integer equals the next largest positive integer."
"Proof: Let P(n) be the proposition ' n=n+1 .' To show that
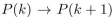
true for some k , so that k=k+1 . Add 1 to both sides of this equation to obtain k+1=k+2 , which is
P(k+1) . Therefore
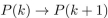
is true. Hence P(n) is true for all positive integers n ."

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
32
give a recursive definition (with initial condition(s)) of 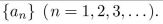
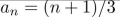
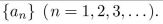
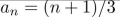

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
33
give a recursive definition with initial condition(s).
The set {. . . , −4, −2, 0, 2, 4, 6, . . .}
The set {. . . , −4, −2, 0, 2, 4, 6, . . .}

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
34
give a recursive definition with initial condition(s).
The function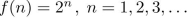
The function
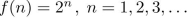

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
35
give a recursive definition (with initial condition(s)) of 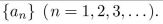
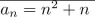
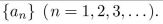
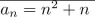

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
36
give a recursive definition with initial condition(s).
The set {1, 1/3, 1/9, 1/27, . . .}
The set {1, 1/3, 1/9, 1/27, . . .}

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
37
give a recursive definition with initial condition(s).
The function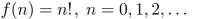
The function

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
38
Let S be the set of positive integers defined by:
Basis step: 4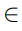 S .
S .
Recursive step: If n 11ecb3f6_226e_1945_8ce8_8160bc243d3a_TB6843_11 S , then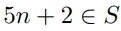 and 11ecb3f6_4662_3346_8ce8_7d38df65e052_TB6843_11
and 11ecb3f6_4662_3346_8ce8_7d38df65e052_TB6843_11
(a) Show that if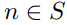 , then
, then 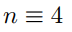 (mod 6).
(mod 6).
(b) Show that there exists an integer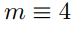 (mod 6) that does not belong to
(mod 6) that does not belong to 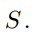
Basis step: 4
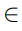 S .
S .Recursive step: If n 11ecb3f6_226e_1945_8ce8_8160bc243d3a_TB6843_11 S , then
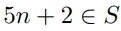 and 11ecb3f6_4662_3346_8ce8_7d38df65e052_TB6843_11
and 11ecb3f6_4662_3346_8ce8_7d38df65e052_TB6843_11(a) Show that if
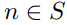 , then
, then 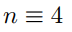 (mod 6).
(mod 6).(b) Show that there exists an integer
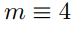 (mod 6) that does not belong to
(mod 6) that does not belong to 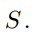

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
39
give a recursive definition with initial condition(s).
The set {0, 3, 6, 9, . . .}
The set {0, 3, 6, 9, . . .}

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
40
give a recursive definition with initial condition(s).
The Fibonacci numbers 1, 1, 2, 3, 5, 8, 13, . . .
The Fibonacci numbers 1, 1, 2, 3, 5, 8, 13, . . .

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
41
give a recursive definition with initial condition(s) of the set S .
{. . . , −5, −3, −1, 1, 3, 5, . . .}
{. . . , −5, −3, −1, 1, 3, 5, . . .}

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
42
give a recursive definition with initial condition(s) of the set S .
{3, 7, 11, 15, 19, 23, . . .}
{3, 7, 11, 15, 19, 23, . . .}

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
43
Verify that the following program segment is correct with respect to the initial assertion T and the final 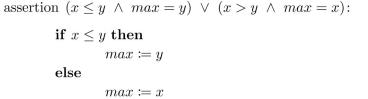 A
A
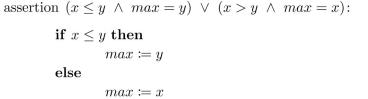 A
A
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
44
Suppose {an} is defined recursively by an = a2n−1 − 1 and that a0 = 2. Find a3 and a4.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
45
Find f(2) and f(3) if f(n) = f(n − 1) · f(n − 2) + 1, f(0) = 1, f(1) = 4.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
46
Consider the following program segment: 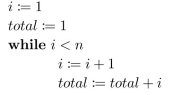 Let p be the proposition
Let p be the proposition 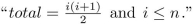 Use mathematical induction to prove that p is a loop invariant.
Use mathematical induction to prove that p is a loop invariant.
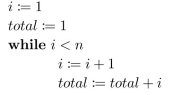 Let p be the proposition
Let p be the proposition 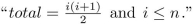 Use mathematical induction to prove that p is a loop invariant.
Use mathematical induction to prove that p is a loop invariant.
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
47
Find f(2) and f(3) if f(n) = f(n − 1)/f(n − 2), f(0) = 2, f(1) = 5.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
48
Verify that the program segment 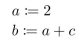 is correct with respect to the initial assertion c = 3 and the final assertion b = 5.
is correct with respect to the initial assertion c = 3 and the final assertion b = 5.
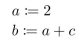 is correct with respect to the initial assertion c = 3 and the final assertion b = 5.
is correct with respect to the initial assertion c = 3 and the final assertion b = 5.
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
49
Find 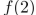 and
and 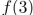 if
if 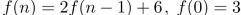
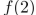 and
and 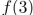 if
if 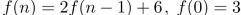

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
50
give a recursive definition with initial condition(s) of the set S .
All positive integer multiples of 5
All positive integer multiples of 5

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
51
give a recursive definition with initial condition(s) of the set S .
The set of strings 1, 111, 11111, 1111111, . . .
The set of strings 1, 111, 11111, 1111111, . . .

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck


