Deck 11: A: Trees
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/94
Play
Full screen (f)
Deck 11: A: Trees
1
fill in the blanks.
If each edge of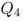 has weight 1, then the cost of any spanning tree of minimum cost is .
has weight 1, then the cost of any spanning tree of minimum cost is .
If each edge of
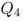 has weight 1, then the cost of any spanning tree of minimum cost is .
has weight 1, then the cost of any spanning tree of minimum cost is .15
2
fill in the blanks.
If T is a full binary tree with 101 vertices, its maximum height is .
If T is a full binary tree with 101 vertices, its maximum height is .
50
3
fill in the blanks.
There are full binary trees with six vertices.
There are full binary trees with six vertices.
0
4
fill in the blanks.
The bubble sort has complexity O( ).
The bubble sort has complexity O( ).

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
5
fill in the blanks.
If T is a full binary tree with 101 vertices, its minimum height is .
If T is a full binary tree with 101 vertices, its minimum height is .

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
6
fill in the blanks.
If T is a full binary tree with 50 leaves, its minimum height is .
If T is a full binary tree with 50 leaves, its minimum height is .

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
7
fill in the blanks.
If T is a full binary tree with 50 internal vertices, then T has vertices.
If T is a full binary tree with 50 internal vertices, then T has vertices.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
8
fill in the blanks.
There are non-isomorphic rooted trees with four vertices.
There are non-isomorphic rooted trees with four vertices.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
9
fill in the blanks.
If T is a binary tree with 100 vertices, its minimum height is .
If T is a binary tree with 100 vertices, its minimum height is .

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
10
fill in the blanks.
If T is a tree with 999 vertices, then T has edges.
If T is a tree with 999 vertices, then T has edges.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
11
fill in the blanks.
Every full binary tree with 61 vertices has leaves.
Every full binary tree with 61 vertices has leaves.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
12
fill in the blanks.
The best comparison-based sorting algorithms for a list of n items have complexity O( ).
The best comparison-based sorting algorithms for a list of n items have complexity O( ).

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
13
fill in the blanks.
The value of the arithmetic expression whose prefix representation is − 5 / · 6 2 − 5 3 is .
The value of the arithmetic expression whose prefix representation is − 5 / · 6 2 − 5 3 is .

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
14
fill in the blanks.
Write 3n − (k + 5) in prefix notation: .
Write 3n − (k + 5) in prefix notation: .

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
15
fill in the blanks.
C7 has spanning trees.
C7 has spanning trees.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
16
fill in the blanks.
Every 3-ary tree with 13 vertices has leaves.
Every 3-ary tree with 13 vertices has leaves.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
17
fill in the blanks.
Every full binary tree with 50 leaves has vertices.
Every full binary tree with 50 leaves has vertices.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
18
fill in the blanks.
There are non-isomorphic trees with four vertices.
There are non-isomorphic trees with four vertices.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
19
fill in the blanks.
The minimum number of weighings with a pan balance scale needed to guarantee that you find the single counterfeit coin and determine whether it is heavier or lighter than the other coins in a group of five coins is .
The minimum number of weighings with a pan balance scale needed to guarantee that you find the single counterfeit coin and determine whether it is heavier or lighter than the other coins in a group of five coins is .

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
20
fill in the blanks.
If T is a full binary tree of height h, then the minimum number of leaves in T is and the maximum number of leaves in T is .
If T is a full binary tree of height h, then the minimum number of leaves in T is and the maximum number of leaves in T is .

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
21
Prove that if T is a full m-ary tree with l leaves, then T has (ml − 1)/(m − 1) vertices.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
22
Draw all nonisomorphic rooted trees with 4 vertices.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
23
fill in the blanks.
Every tree is bipartite.
Every tree is bipartite.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
24
fill in the blanks.
There is a tree with degrees 3, 3, 2, 2, 1, 1, 1, 1.
There is a tree with degrees 3, 3, 2, 2, 1, 1, 1, 1.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
25
fill in the blanks.
There is a tree with degrees 3, 2, 2, 2, 1, 1, 1, 1, 1.
There is a tree with degrees 3, 2, 2, 2, 1, 1, 1, 1, 1.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
26
fill in the blanks.
Every full 3-ary tree of height 2 has at least vertices and at most vertices.
Every full 3-ary tree of height 2 has at least vertices and at most vertices.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
27
fill in the blanks.
If T is a tree with 17 vertices, then there is a simple path in T of length 17.
If T is a tree with 17 vertices, then there is a simple path in T of length 17.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
28
fill in the blanks.
If T is a tree, then its vertex-chromatic number is and its region-chromatic number is .
If T is a tree, then its vertex-chromatic number is and its region-chromatic number is .

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
29
Suppose T is a full m-ary tree with l leaves. Prove that T has (l − 1)/(m − 1) internal vertices.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
30
fill in the blanks.
If two trees have the same number of vertices and the same degrees, then the two trees are isomorphic.
If two trees have the same number of vertices and the same degrees, then the two trees are isomorphic.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
31
fill in the blanks.
The largest number of leaves in a binary tree of height 5 is .
The largest number of leaves in a binary tree of height 5 is .

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
32
fill in the blanks.
If T is a tree with 50 vertices, the largest degree that any vertex can have is 49.
If T is a tree with 50 vertices, the largest degree that any vertex can have is 49.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
33
fill in the blanks.
There are full 3-ary trees with 6 vertices.
There are full 3-ary trees with 6 vertices.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
34
fill in the blanks.
No tree has a Hamilton path.
No tree has a Hamilton path.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
35
fill in the blanks.
Every full binary tree with 45 vertices has internal vertices.
Every full binary tree with 45 vertices has internal vertices.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
36
fill in the blanks.
In a binary tree with 16 vertices, there must be a path of length 4.
In a binary tree with 16 vertices, there must be a path of length 4.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
37
fill in the blanks.
Every tree is planar.
Every tree is planar.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
38
Suppose T is a full m-ary tree with i internal vertices. Prove that T has 1 + (m − 1)i leaves.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
39
Draw all nonisomorphic trees with 5 vertices.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
40
fill in the blanks.
A full 3-ary tree with 13 internal vertices has vertices.
A full 3-ary tree with 13 internal vertices has vertices.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
41
(a) Set up a binary tree for the following list, in the given order, using alphabetical ordering: SHE, SELLS, SEA, SHELLS, BY, THE, SEASHORE. (b) How many comparisons with words in the tree are needed to determine if the word SHARK is in the tree? (c) How many comparisons with words in the tree are needed to determine if the word SEAWEED is in the tree? (d) How many comparisons with words in the tree are needed to determine if the word SHELLS is in the tree?

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
42
(a) Set up a binary tree for the following list, in the given order, using alphabetical ordering: STOP, LET, THERE, TAPE, NONE, YOU, ANT, NINE, OAT, NUT. (b) Explain step by step how you would search for the word TEST in your tree. (c) What is the height of the shortest binary search tree that can hold all 10 words? (d) Write the preorder traversal of the tree. (e) Write the postorder traversal of the tree. (f) Write the inorder traversal of the tree.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
43
Find the inorder traversal. Questions 53-55 refer to the tree at the right. 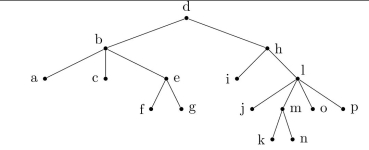


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
44
Find the preorder traversal.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
45
Write the compound proposition 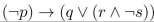 in postfix notation.
in postfix notation.
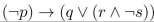 in postfix notation.
in postfix notation.
Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
46
Prove that if T is a full m-ary tree with v vertices, then T has ((m − 1)v + 1)/m leaves.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
47
Find the inorder traversal of the parsing tree for 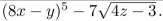
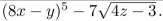

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
48
Suppose that the universal address set address of a vertex v in an ordered rooted tree is 3.2.5.1.5. Find (a) the level of v. (b) the minimum number of siblings of v. (c) the address of the parent of v. (d) the minimum number of vertices in the tree.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
49
Draw a parsing tree for (a − (3 + 2b))/(c2 +
d).
d).

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
50
The string  is postfix notation for an algebraic expression. Write the expression in prefix notation.
is postfix notation for an algebraic expression. Write the expression in prefix notation.
 is postfix notation for an algebraic expression. Write the expression in prefix notation.
is postfix notation for an algebraic expression. Write the expression in prefix notation.
Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
51
The algebraic expression  is written in prefix notation. Write the expression in postfix notation.
is written in prefix notation. Write the expression in postfix notation.
 is written in prefix notation. Write the expression in postfix notation.
is written in prefix notation. Write the expression in postfix notation.
Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
52
Write the compound proposition 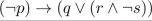 in prefix notation.
in prefix notation.
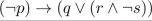 in prefix notation.
in prefix notation.
Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
53
Suppose you have 5 coins, one of which is heavier than the other four. Draw the decision tree for using a pan balance scale to find the heavy coin.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
54
Write the compound proposition  in infix notation.
in infix notation.
 in infix notation.
in infix notation.
Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
55
Suppose you have 50 coins, one of which is counterfeit (either heavier or lighter than the others). You use a pan balance scale to find the bad coin. Prove that 4 weighings are not enough to guarantee that you find the bad coin and determine whether it is heavier or lighter than the other coins.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
56
Find the postorder traversal of the parsing tree for 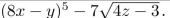

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
57
Find the postorder traversal.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
58
Suppose you have 5 coins, one of which is counterfeit (either heavier or lighter than the other four). You use a pan balance scale to find the bad coin and determine whether it is heavier or lighter. (a) Prove that 2 weighings are not enough to guarantee that you find the bad coin and determine whether it is heavier or lighter. (b) Draw a decision tree for weighing the coins to determine the bad coin (and whether it is heavier or lighter) in the minimum number of weighings.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
59
Find the preorder traversal of the parsing tree for 


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
60
The string 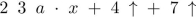 is postfix notation for an algebraic expression. Write the expression in infix notation.
is postfix notation for an algebraic expression. Write the expression in infix notation.
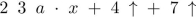 is postfix notation for an algebraic expression. Write the expression in infix notation.
is postfix notation for an algebraic expression. Write the expression in infix notation.
Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
61
Using alphabetical ordering, find a spanning tree for this graph by using a breadth-first search.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
62
Find the value of 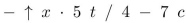 (in prefix notation) if
(in prefix notation) if 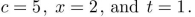 Questions 66-73 refer to this graph.
Questions 66-73 refer to this graph. 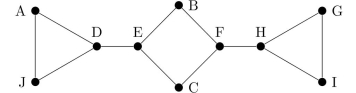
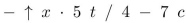 (in prefix notation) if
(in prefix notation) if 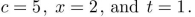 Questions 66-73 refer to this graph.
Questions 66-73 refer to this graph. 

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
63
Using alphabetical ordering, find a spanning tree for this graph by using a depth-first search.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
64
The string 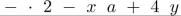 is prefix notation for an algebraic expression. Write the expression in postfix notation.
is prefix notation for an algebraic expression. Write the expression in postfix notation.
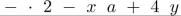 is prefix notation for an algebraic expression. Write the expression in postfix notation.
is prefix notation for an algebraic expression. Write the expression in postfix notation.
Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
65
The string 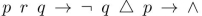 is postfix notation for a logic expression; however, there is a misprint. The triangle should be one of these three:
is postfix notation for a logic expression; however, there is a misprint. The triangle should be one of these three: 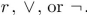 Determine which of these three it must be and explain your reasoning.
Determine which of these three it must be and explain your reasoning.
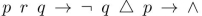 is postfix notation for a logic expression; however, there is a misprint. The triangle should be one of these three:
is postfix notation for a logic expression; however, there is a misprint. The triangle should be one of these three: 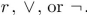 Determine which of these three it must be and explain your reasoning.
Determine which of these three it must be and explain your reasoning.
Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
66
Using reverse alphabetical ordering, find a spanning tree for the graph by using a depth-first search.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
67
The string 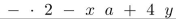 is prefix notation for an algebraic expression. Write the expression in infix notation.
is prefix notation for an algebraic expression. Write the expression in infix notation.
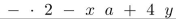 is prefix notation for an algebraic expression. Write the expression in infix notation.
is prefix notation for an algebraic expression. Write the expression in infix notation.
Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
68
Find a spanning tree for the graph K3,4 using a depth-first search. (Assume that the vertices are labeled u1, u2, u3 in one set and v1, v2, v3, v4 in the other set, and that alphabetical ordering is used in the search, with numerical ordering on the subscripts used to break ties.)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
69
Using the ordering B, G, J, A, C, I, F, H, D, E, find a spanning tree for this graph by using a depth-first search.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
70
Using the ordering C, D, E, F, G, H, I, J, A, B, C, find a spanning tree for this graph by using a breadth-first search.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
71
Using alphabetical ordering, find a spanning tree for this graph by using a depth-first search.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
72
Using the ordering B, G, J, A, C, I, F, H, D, E, find a spanning tree for this graph by using a depth-first search.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
73
Using the ordering C, D, E, F, G, H, I, J, A, B, C, find a spanning tree for this graph by using a depth-first search.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
74
Using the ordering C, D, E, F, G, H, I, J, A, B, C, find a spanning tree for this graph by using a depth-first search.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
75
Using reverse alphabetical ordering, find a spanning tree for the graph by using a depth-first search.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
76
Using the ordering B, G, J, A, C, I, F, H, D, E, find a spanning tree for this graph by using a breadth-first search. Questions 74-81 refer to this graph. 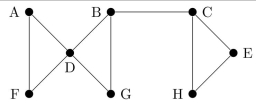


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
77
Using reverse alphabetical ordering, find a spanning tree for the graph by using a breadth-first search.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
78
Using the ordering C, D, E, F, G, H, I, J, A, B, C, find a spanning tree for this graph by using a breadth-first search.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
79
Using reverse alphabetical ordering, find a spanning tree for the graph by using a breadth-first search.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
80
Using the ordering B, G, J, A, C, I, F, H, D, E, find a spanning tree for this graph by using a breadth-first search.

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck


