Exam 11: A: Trees
Exam 1: The Foundations: Logic and Proofs18 Questions
Exam 1: A: the Foundations: Logic and Proofs201 Questions
Exam 2: Basic Structures: Sets, Functions, Sequences, Sums, Matrices5 Questions
Exam 2: A: Basic Structures: Sets, Functions, Sequences, Sums, Matrices210 Questions
Exam 3: Algorithms8 Questions
Exam 3: A: Algorithms54 Questions
Exam 4: Number Theory and Cryptography10 Questions
Exam 4: A: Number Theory and Cryptography149 Questions
Exam 5: Induction and Recursion10 Questions
Exam 5: A: Induction and Recursion51 Questions
Exam 6: Counting14 Questions
Exam 6: A: Counting155 Questions
Exam 7: Discrete Probability9 Questions
Exam 7: A: Discrete Probability50 Questions
Exam 8: Advanced Counting Techniques16 Questions
Exam 8: A: Advanced Counting Techniques124 Questions
Exam 9: Relations13 Questions
Exam 9: A: Relations72 Questions
Exam 10: Graphs14 Questions
Exam 10: A: Graphs131 Questions
Exam 11: Trees13 Questions
Exam 11: A: Trees94 Questions
Exam 12: Boolean Algebra11 Questions
Exam 12: A: Boolean Algebra67 Questions
Exam 13: Modeling Computation14 Questions
Exam 13: A: Modeling Computation67 Questions
Exam 14: Mathematics Problem Set: Set Theory, Number Theory, Combinatorics, and Boolean Algebra29 Questions
Select questions type
Find a spanning tree of minimum cost for this graph. 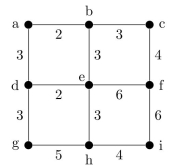
Free
(Essay)
4.7/5  (41)
(41)
Correct Answer:
The minimum weight is 24. One example of a tree is 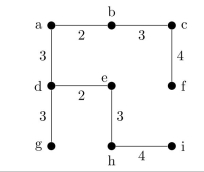
refer to this graph. 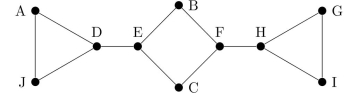 -Using alphabetical ordering, find a spanning tree for this graph by using a depth-first search.
-Using alphabetical ordering, find a spanning tree for this graph by using a depth-first search.
Free
(Essay)
4.8/5  (36)
(36)
Correct Answer:
Suppose you have 5 coins, one of which is counterfeit (either heavier or lighter than the other four). You use a pan balance scale to find the bad coin and determine whether it is heavier or lighter.
(a) Prove that 2 weighings are not enough to guarantee that you find the bad coin and determine whether it is heavier or lighter.
(b) Draw a decision tree for weighing the coins to determine the bad coin (and whether it is heavier or lighter) in the minimum number of weighings.
Free
(Essay)
4.8/5  (36)
(36)
Correct Answer:
(a) Two weighings yield a 3-ary tree of height 2, which has at most 9 leaves, but 5 coins require a tree with 10 leaves.
(b) Use the weighing 1 and 2 against 3 and 4 as the root. If the four coins have the same weight, weigh 1 against 5 to determine whether 5 is heavy or light. If 1 and 2 are lighter or heavier than 3 and 4, weigh 1 against 2. If 1 and 2 balance, weigh 3 against 4 to find out which of these coins is heavier or lighter; if 1 and 2 do not balance, then immediate information is obtained regarding coins 1 or 2. (The "<" symbol on an edge means that the coins in the left pan weigh less than the coins in the right pan.) 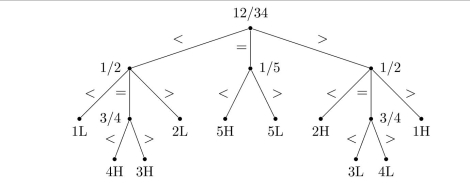
Find a spanning tree for the graph K3,4 using a breadth-first search. (Assume that the vertices are labeled in one set and in the other set, and that alphabetical ordering is used in the search, with numerical ordering on the subscripts used to break ties.)
(Essay)
4.7/5  (38)
(38)
Use the merge sort to sort the list 3, 8, 12, 4, 1, 5, 9, 6 in increasing order.
(Essay)
4.8/5  (38)
(38)
fill in the blanks.
-Every full binary tree with 45 vertices has ____ internal vertices.
(Short Answer)
4.8/5  (37)
(37)
refer to this graph.  -Using reverse alphabetical ordering, find a spanning tree for the graph by using a breadth-first search.
-Using reverse alphabetical ordering, find a spanning tree for the graph by using a breadth-first search.
(Essay)
4.7/5  (32)
(32)
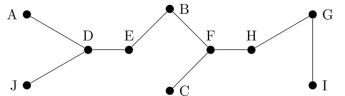
refer to this graph.  -Using the ordering C, D, E, F, G, H, I, J, A, B, C, find a spanning tree for this graph by using a breadth-first search.
-Using the ordering C, D, E, F, G, H, I, J, A, B, C, find a spanning tree for this graph by using a breadth-first search.
(Essay)
4.9/5  (28)
(28)
refer to this graph.  -Using alphabetical ordering, find a spanning tree for this graph by using a breadth-first search.
-Using alphabetical ordering, find a spanning tree for this graph by using a breadth-first search.
(Essay)
4.8/5  (41)
(41)
fill in the blanks.
-If each edge of has weight 1, then the cost of any spanning tree of minimum cost is ____.
(Short Answer)
4.9/5  (40)
(40)
Use backtracking to find a sum of integers in the set {18, 19, 23, 25, 31} that equals 44.
(Essay)
4.8/5  (31)
(31)
Use the merge sort to sort the list 4, 8, 6, 1, 5, 7, 3, 2 in increasing order.
(Essay)
5.0/5  (29)
(29)
The string is postfix notation for a logic expression; however, there is a misprint. The triangle should be one of these three: Determine which of these three it must be and explain your reasoning.
(Essay)
4.8/5  (31)
(31)
fill in the blanks.
-The minimum number of weighings with a pan balance scale needed to guarantee that you find the single counterfeit coin and determine whether it is heavier or lighter than the other coins in a group of five coins is ____.
(Short Answer)
4.8/5  (37)
(37)
fill in the blanks.
-If T is a full binary tree with 50 leaves, its minimum height is ____.
(Short Answer)
4.7/5  (41)
(41)
(a) Set up a binary tree for the following list, in the given order, using alphabetical ordering: SHE, SELLS, SEA, SHELLS, BY, THE, SEASHORE.
(b) How many comparisons with words in the tree are needed to determine if the word SHARK is in the tree?
(c) How many comparisons with words in the tree are needed to determine if the word SEAWEED is in the tree?
(d) How many comparisons with words in the tree are needed to determine if the word SHELLS is in the tree?
(Essay)
4.9/5  (36)
(36)
fill in the blanks.
-There are ____ full 3-ary trees with 6 vertices.
(Short Answer)
4.9/5  (38)
(38)
Describe the difference between Prim's algorithm and Kruskal's algorithm for finding a spanning tree of minimum cost.
(Essay)
4.9/5  (42)
(42)
Showing 1 - 20 of 94
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)