Deck 6: Matrices and Determinants
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/152
Play
Full screen (f)
Deck 6: Matrices and Determinants
1
Use Matrices and Gaussian Elimination to Solve Systems
Solve the system of equations using matrices. Use Gaussian elimination with back-substitution.
A)
B)
C)
D)
Solve the system of equations using matrices. Use Gaussian elimination with back-substitution.
A)
B)
C)
D)
A
2
Use Matrices and Gauss-Jordan Elimination to Solve Systems
Solve the system of equations using matrices. Use Gauss-Jordan elimination.
A)
B)
C)
D)
Solve the system of equations using matrices. Use Gauss-Jordan elimination.
A)
B)
C)
D)
A
3
Write the system of linear equations represented by the augmented matrix. Use x, y, z, and, if necessary, w for the
variables. Then use back-substitution to find the solution.
A)
B)
C)
D)
variables. Then use back-substitution to find the solution.
A)
B)
C)
D)
A
4
Use Matrices and Gaussian Elimination to Solve Systems
Solve the system of equations using matrices. Use Gaussian elimination with back-substitution.
A)
B)
C)
D)
Solve the system of equations using matrices. Use Gaussian elimination with back-substitution.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
5
Use Matrices and Gauss-Jordan Elimination to Solve Systems
Solve the system of equations using matrices. Use Gauss-Jordan elimination.
A)
B)
C)
D)
Solve the system of equations using matrices. Use Gauss-Jordan elimination.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
6
Write the system of linear equations represented by the augmented matrix. Use x, y, z, and, if necessary, w for the
variables.
A)
B)
C)
D)
variables.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
7
Write the system of linear equations represented by the augmented matrix. Use x, y, z, and, if necessary, w for the
variables.
A)
B)
C)
D)
variables.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
8
Use Matrices and Gauss-Jordan Elimination to Solve Systems
Solve the system of equations using matrices. Use Gauss-Jordan elimination.
A)
B)
C)
D)
Solve the system of equations using matrices. Use Gauss-Jordan elimination.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
9
Write the system of linear equations represented by the augmented matrix. Use x, y, z, and, if necessary, w for the
variables. Then use back-substitution to find the solution.
A)
В)
C)
D)
variables. Then use back-substitution to find the solution.
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
10
Use Matrices and Gaussian Elimination to Solve Systems
Solve the system of equations using matrices. Use Gaussian elimination with back-substitution.
A)
B)
C)
D)
Solve the system of equations using matrices. Use Gaussian elimination with back-substitution.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
11
Write the system of linear equations represented by the augmented matrix. Use x, y, z, and, if necessary, w for the
variables. Then use back-substitution to find the solution.
A)
B)
C)
D)
variables. Then use back-substitution to find the solution.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
12
Write the augmented matrix for the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
13
Use Matrices and Gaussian Elimination to Solve Systems
Solve the system of equations using matrices. Use Gaussian elimination with back-substitution.
A)
B)
C)
D)
Solve the system of equations using matrices. Use Gaussian elimination with back-substitution.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
14
Perform the matrix row operation (or operations)and write the new matrix.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
15
Use Matrices and Gaussian Elimination to Solve Systems
Solve the system of equations using matrices. Use Gaussian elimination with back-substitution.
A)
B)
C)
D)
Solve the system of equations using matrices. Use Gaussian elimination with back-substitution.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
16
Write the augmented matrix for the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
17
Write the system of linear equations represented by the augmented matrix. Use x, y, z, and, if necessary, w for the
variables.
A)
B)
C)
D)
variables.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
18
Write the augmented matrix for the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
19
Perform the matrix row operation (or operations)and write the new matrix.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
20
Perform the matrix row operation (or operations)and write the new matrix.
![Perform the matrix row operation (or operations)and write the new matrix. \left[ \begin{array} { r r r | r } 1 & - 4 & 1 & 3 \\ - 5 & 0 & 3 & - 3 \\ - 1 & 2 & - 2 & - 1 \end{array} \right] - 3 R _ { 1 } + R _ { 2 }](https://storage.examlex.com/TB1195/11ecbbe7_d8e6_b3eb_8887_919685d2ca4e_TB1195_00.jpg)
![Perform the matrix row operation (or operations)and write the new matrix. \left[ \begin{array} { r r r | r } 1 & - 4 & 1 & 3 \\ - 5 & 0 & 3 & - 3 \\ - 1 & 2 & - 2 & - 1 \end{array} \right] - 3 R _ { 1 } + R _ { 2 }](https://storage.examlex.com/TB1195/11ecbbe7_d8e6_b3eb_8887_919685d2ca4e_TB1195_00.jpg)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
21
Apply Gaussian Elimination to Systems Without Unique Solutions
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
22
Apply Gaussian Elimination to Systems Without Unique Solutions
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
23
Apply Gaussian Elimination to Systems with More Variables than Equations
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
24
Apply Gaussian Elimination to Systems Without Unique Solutions
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
25
Apply Gaussian Elimination to Systems with More Variables than Equations
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
26
Apply Gaussian Elimination to Systems Without Unique Solutions
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
27
Use Matrices and Gauss-Jordan Elimination to Solve Systems
Solve the system of equations using matrices. Use Gauss-Jordan elimination.
A)
B)
C)
D)
Solve the system of equations using matrices. Use Gauss-Jordan elimination.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
28
Write a system of linear equations in three variables, and then use matrices to solve the system.
Ron attends a cocktail party (with his graphing calculator in his pocket). He wants to limit his food intake to 131 g protein, 107 g fat, and 165 g carbohydrate. According to the health conscious hostess, the
Marinated mushroom caps have 3 g protein, 5 g fat, and 9 g carbohydrate; the spicy meatballs have 14 g
Protein, 7 g fat, and 15 g carbohydrate; and the deviled eggs have 13 g protein, 15 g fat, and 6 g
Carbohydrate. How many of each snack can he eat to obtain his goal?
A)7 mushrooms; 6 meatballs; 2 eggs
B)6 mushrooms; 2 meatballs; 7 eggs
C)2 mushrooms; 7 meatballs; 6 eggs
D)8 mushrooms; 7 meatballs; 3 eggs
Ron attends a cocktail party (with his graphing calculator in his pocket). He wants to limit his food intake to 131 g protein, 107 g fat, and 165 g carbohydrate. According to the health conscious hostess, the
Marinated mushroom caps have 3 g protein, 5 g fat, and 9 g carbohydrate; the spicy meatballs have 14 g
Protein, 7 g fat, and 15 g carbohydrate; and the deviled eggs have 13 g protein, 15 g fat, and 6 g
Carbohydrate. How many of each snack can he eat to obtain his goal?
A)7 mushrooms; 6 meatballs; 2 eggs
B)6 mushrooms; 2 meatballs; 7 eggs
C)2 mushrooms; 7 meatballs; 6 eggs
D)8 mushrooms; 7 meatballs; 3 eggs

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
29
Apply Gaussian Elimination to Systems with More Variables than Equations
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
30
Use Matrices and Gauss-Jordan Elimination to Solve Systems
Solve the system of equations using matrices. Use Gauss-Jordan elimination.
A)
B)
C)
D)
Solve the system of equations using matrices. Use Gauss-Jordan elimination.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
31
Apply Gaussian Elimination to Systems Without Unique Solutions
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
32
Apply Gaussian Elimination to Systems with More Variables than Equations
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
33
Write a system of linear equations in three variables, and then use matrices to solve the system.
The table below shows the number of birds for three selected years after an endangered species protection program was started.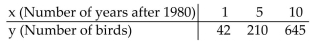
Use the quadratic function to model the data. Solve the system of linear equations involving , and using matrices. Find the equation that models the data.
A)
B)
C)
D)
The table below shows the number of birds for three selected years after an endangered species protection program was started.
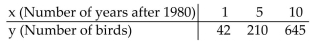
Use the quadratic function to model the data. Solve the system of linear equations involving , and using matrices. Find the equation that models the data.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
34
Apply Gaussian Elimination to Systems Without Unique Solutions
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
35
Write a system of linear equations in three variables, and then use matrices to solve the system.
A ceramics workshop makes wreaths, trees, and sleighs for sale at Christmas. A wreath takes 3 hours to prepare, 2 hours to paint, and 10 hours to fire. A tree takes 15 hours to prepare, 3 hours to paint, and 4
Hours to fire. A sleigh takes 4 hours to prepare, 16 hours to paint, and 7 hours to fire. If the workshop has
93 hours for prep time, 74 hours for painting, and 107 hours for firing, how many of each can be made?
A)7 wreaths; 4 trees; 3 sleighs
B)4 wreaths; 3 trees; 7 sleighs
C)3 wreaths; 7 trees; 4 sleighs
D)8 wreaths; 5 trees; 4 sleighs
A ceramics workshop makes wreaths, trees, and sleighs for sale at Christmas. A wreath takes 3 hours to prepare, 2 hours to paint, and 10 hours to fire. A tree takes 15 hours to prepare, 3 hours to paint, and 4
Hours to fire. A sleigh takes 4 hours to prepare, 16 hours to paint, and 7 hours to fire. If the workshop has
93 hours for prep time, 74 hours for painting, and 107 hours for firing, how many of each can be made?
A)7 wreaths; 4 trees; 3 sleighs
B)4 wreaths; 3 trees; 7 sleighs
C)3 wreaths; 7 trees; 4 sleighs
D)8 wreaths; 5 trees; 4 sleighs

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
36
Apply Gaussian Elimination to Systems Without Unique Solutions
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
37
Apply Gaussian Elimination to Systems Without Unique Solutions
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
38
Write a system of linear equations in three variables, and then use matrices to solve the system.
There were approximately 100,000 vehicles sold at a particular dealership last year. The dealer tracks sales by age group for marketing purposes. The percentage of 36- to 59-year-old buyers and the percentage of
Buyers 60 and older combined exceeds the percentage of buyers 35 and younger by 38%. If the percentage
Of buyers in the oldest group is doubled, it is 24% less than the percentage of users in the middle group.
Find the percentage of buyers in each of the three age groups.
A)31% 35 and younger; 54% 36-59 year olds; 15% 60 and older
B)33% 35 and younger; 51% 36-59 year olds; 16% 60 and older
C)25% 35 and younger; 56% 36-59 year olds; 19% 60 and older
D)15% 35 and younger; 54% 36-59 year olds; 31% 60 and older
There were approximately 100,000 vehicles sold at a particular dealership last year. The dealer tracks sales by age group for marketing purposes. The percentage of 36- to 59-year-old buyers and the percentage of
Buyers 60 and older combined exceeds the percentage of buyers 35 and younger by 38%. If the percentage
Of buyers in the oldest group is doubled, it is 24% less than the percentage of users in the middle group.
Find the percentage of buyers in each of the three age groups.
A)31% 35 and younger; 54% 36-59 year olds; 15% 60 and older
B)33% 35 and younger; 51% 36-59 year olds; 16% 60 and older
C)25% 35 and younger; 56% 36-59 year olds; 19% 60 and older
D)15% 35 and younger; 54% 36-59 year olds; 31% 60 and older

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
39
Apply Gaussian Elimination to Systems Without Unique Solutions
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
40
Apply Gaussian Elimination to Systems Without Unique Solutions
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the problem.
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the problem.
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
43
Give the order of the matrix, and identify the given element of the matrix.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the problem.
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the problem.
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the problem.
Let . Find .
A)
C)
D)
Let . Find .
A)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
47
Understand What is Meant by Equal Matrices
Find values for the variables so that the matrices are equal.
B)
A)
D)
C)
Find values for the variables so that the matrices are equal.
B)
A)
D)
C)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
48
Apply Gaussian Elimination to Systems with More Variables than Equations
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
49
Understand What is Meant by Equal Matrices
Find values for the variables so that the matrices are equal.
A)
B)
C)
D)
Find values for the variables so that the matrices are equal.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
50
Solve Problems Involving Systems Without Unique Solutions
Solve the problem using matrices.
The figure below shows the intersection of three one-way streets. To keep traffic moving, the number of cars per minute entering an intersection must equal the number of cars leaving that intersection. Set up a
System of equations that keeps traffic moving, and use Gaussian elimination to solve the system. If
Construction limits z to t cars per minute, how many cars per minute must pass through the other
Intersections to keep traffic moving?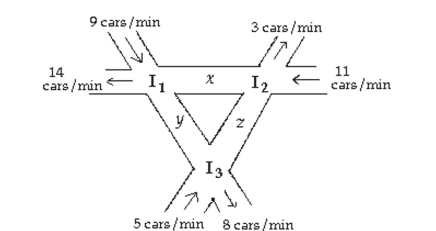
A) cars between and between and
B) cars between and between and
C) cars between and cars/min between and
D) cars between and between and
Solve the problem using matrices.
The figure below shows the intersection of three one-way streets. To keep traffic moving, the number of cars per minute entering an intersection must equal the number of cars leaving that intersection. Set up a
System of equations that keeps traffic moving, and use Gaussian elimination to solve the system. If
Construction limits z to t cars per minute, how many cars per minute must pass through the other
Intersections to keep traffic moving?

A) cars between and between and
B) cars between and between and
C) cars between and cars/min between and
D) cars between and between and

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
51
Solve Problems Involving Systems Without Unique Solutions
Solve the problem using matrices.
The nutritional content per ounce for three foods is given in the table below.
What combination of these foods can provide exactly 14 grams of fat, 27 grams of protein, and 10 grams of fiber?
A) No possible combination of these foods
B) 3 oz of Food A; 5 oz of Food B; 1 oz of Food
C) of Food A; 7 oz of Food B; 1 oz of Food
D) of Food of Food B; 2 oz of Food
Solve the problem using matrices.
The nutritional content per ounce for three foods is given in the table below.

What combination of these foods can provide exactly 14 grams of fat, 27 grams of protein, and 10 grams of fiber?
A) No possible combination of these foods
B) 3 oz of Food A; 5 oz of Food B; 1 oz of Food
C) of Food A; 7 oz of Food B; 1 oz of Food
D) of Food of Food B; 2 oz of Food

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
52
Solve the problem.
Let . Find .
A)
B)
C)
D)
Let . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
53
Give the order of the matrix, and identify the given element of the matrix.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
54
Understand What is Meant by Equal Matrices
Find values for the variables so that the matrices are equal.
A)
B)
C)
D)
Find values for the variables so that the matrices are equal.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the problem.
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
56
Solve the problem.
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
57
Understand What is Meant by Equal Matrices
Find values for the variables so that the matrices are equal.
A)
B)
C)
D)
Find values for the variables so that the matrices are equal.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
58
Solve the problem.
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
59
Solve the problem.
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
60
Solve Problems Involving Systems Without Unique Solutions
Solve the problem using matrices.
A company that manufactures products A, B, and C does both assembly and testing. The hours needed to assemble and test each product are shown in the table below.
The company has exactly 24 hours per week available for assembly and 109 hours per week available for testing. If the company must produce units of Product this week, how many units of Products and can they produce?
A) 11 of Product A; of Product B
B) 11t of Product A; 2t of Product B
C) of Product of Product
D) 11 of Product of Product
Solve the problem using matrices.
A company that manufactures products A, B, and C does both assembly and testing. The hours needed to assemble and test each product are shown in the table below.

The company has exactly 24 hours per week available for assembly and 109 hours per week available for testing. If the company must produce units of Product this week, how many units of Products and can they produce?
A) 11 of Product A; of Product B
B) 11t of Product A; 2t of Product B
C) of Product of Product
D) 11 of Product of Product

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the problem.
Let and . Find
A)
B)
C)
D)
Let and . Find
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
62
Find the product AB, if possible.
A)
B)
C)
A)
B)
C)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
63
Solve the matrix equation for X.
Let and
A)
B)
C)
D)
Let and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
64
Model Applied Situations with Matrix Operations
The shape in the figure below is shown using 9 pixels in a grid. The color levels are given to the right of the figure. Use the matrix that represents a digital photograph of the shape to solve the problem.![Model Applied Situations with Matrix Operations The \perp shape in the figure below is shown using 9 pixels in a 3 \times 3 grid. The color levels are given to the right of the figure. Use the matrix \left[ \begin{array} { l l l } 1 & 3 & 1 \\ 1 & 3 & 1 \\ 3 & 3 & 3 \end{array} \right] that represents a digital photograph of the \perp shape to solve the problem. Adjust the contrast by changing the black to dark grey and the light grey to white. Use matrix addition to accomplish this. A) \left[ \begin{array} { l l l } 1 & 3 & 1 \\ 1 & 3 & 1 \\ 3 & 3 & 3 \end{array} \right] + \left[ \begin{array} { l l l } - 1 & - 1 & - 1 \\ - 1 & - 1 & - 1 \\ - 1 & - 1 & - 1 \end{array} \right] = \left[ \begin{array} { l l l } 0 & 2 & 0 \\ 0 & 2 & 0 \\ 2 & 2 & 2 \end{array} \right] B) \left[ \begin{array} { l l l } 1 & 3 & 1 \\ 1 & 3 & 1 \\ 3 & 3 & 3 \end{array} \right] + \left[ \begin{array} { r r r } 0 & - 1 & 0 \\ 0 & - 1 & 0 \\ - 1 & - 1 & - 1 \end{array} \right] = \left[ \begin{array} { l l l } 1 & 2 & 1 \\ 1 & 2 & 1 \\ 2 & 2 & 2 \end{array} \right] C) \left[ \begin{array} { l l l } 1 & 3 & 1 \\ 1 & 3 & 1 \\ 3 & 3 & 3 \end{array} \right] + \left[ \begin{array} { l l l } 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array} \right] = \left[ \begin{array} { l l l } 2 & 4 & 2 \\ 2 & 4 & 2 \\ 4 & 4 & 4 \end{array} \right] D) \left[ \begin{array} { l l l } 1 & 3 & 1 \\ 1 & 3 & 1 \\ 3 & 3 & 3 \end{array} \right] + \left[ \begin{array} { r r r } 0 & - 1 & 0 \\ 0 & - 1 & 0 \\ - 1 & - 1 & - 1 \end{array} \right] = \left[ \begin{array} { l l l } 0 & 2 & 0 \\ 0 & 2 & 0 \\ 2 & 2 & 2 \end{array} \right]](https://storage.examlex.com/TB1195/11eb4a02_a36a_13b8_9e74_addeab623e08_TB1195_00.jpg)
Adjust the contrast by changing the black to dark grey and the light grey to white. Use matrix addition to accomplish this. A)
B)
C)
D)
The shape in the figure below is shown using 9 pixels in a grid. The color levels are given to the right of the figure. Use the matrix that represents a digital photograph of the shape to solve the problem.
![Model Applied Situations with Matrix Operations The \perp shape in the figure below is shown using 9 pixels in a 3 \times 3 grid. The color levels are given to the right of the figure. Use the matrix \left[ \begin{array} { l l l } 1 & 3 & 1 \\ 1 & 3 & 1 \\ 3 & 3 & 3 \end{array} \right] that represents a digital photograph of the \perp shape to solve the problem. Adjust the contrast by changing the black to dark grey and the light grey to white. Use matrix addition to accomplish this. A) \left[ \begin{array} { l l l } 1 & 3 & 1 \\ 1 & 3 & 1 \\ 3 & 3 & 3 \end{array} \right] + \left[ \begin{array} { l l l } - 1 & - 1 & - 1 \\ - 1 & - 1 & - 1 \\ - 1 & - 1 & - 1 \end{array} \right] = \left[ \begin{array} { l l l } 0 & 2 & 0 \\ 0 & 2 & 0 \\ 2 & 2 & 2 \end{array} \right] B) \left[ \begin{array} { l l l } 1 & 3 & 1 \\ 1 & 3 & 1 \\ 3 & 3 & 3 \end{array} \right] + \left[ \begin{array} { r r r } 0 & - 1 & 0 \\ 0 & - 1 & 0 \\ - 1 & - 1 & - 1 \end{array} \right] = \left[ \begin{array} { l l l } 1 & 2 & 1 \\ 1 & 2 & 1 \\ 2 & 2 & 2 \end{array} \right] C) \left[ \begin{array} { l l l } 1 & 3 & 1 \\ 1 & 3 & 1 \\ 3 & 3 & 3 \end{array} \right] + \left[ \begin{array} { l l l } 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array} \right] = \left[ \begin{array} { l l l } 2 & 4 & 2 \\ 2 & 4 & 2 \\ 4 & 4 & 4 \end{array} \right] D) \left[ \begin{array} { l l l } 1 & 3 & 1 \\ 1 & 3 & 1 \\ 3 & 3 & 3 \end{array} \right] + \left[ \begin{array} { r r r } 0 & - 1 & 0 \\ 0 & - 1 & 0 \\ - 1 & - 1 & - 1 \end{array} \right] = \left[ \begin{array} { l l l } 0 & 2 & 0 \\ 0 & 2 & 0 \\ 2 & 2 & 2 \end{array} \right]](https://storage.examlex.com/TB1195/11eb4a02_a36a_13b8_9e74_addeab623e08_TB1195_00.jpg)
Adjust the contrast by changing the black to dark grey and the light grey to white. Use matrix addition to accomplish this. A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
65
Find the product AB, if possible.
A)
B) is not defined.
C)
D)
A)
B) is not defined.
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
66
Find the product AB, if possible.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
67
Solve the matrix equation for X.
Let and
A)
B)
C)
D)
Let and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
68
Solve the matrix equation for X.
Let and
A)
B)
C)
D)
Let and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
69
Find the product AB, if possible.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
70
Find the product AB, if possible.
A)
B) is not defined.
C)
D)
A)
B) is not defined.
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
71
Find the product AB, if possible.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
72
Solve the matrix equation for X.
Let and
A)
B)
C)
D)
Let and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
73
Find the product AB, if possible.
A)
B) is not defined.
C)
D)
A)
B) is not defined.
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
74
Solve the problem.
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
75
Find the product AB, if possible.
A) is not defined.
B)
C)
D)
A) is not defined.
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
76
Solve the matrix equation for X.
Let and
A)
B)
C)
D)
Let and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
77
Find the product AB, if possible.
A) is not defined.
B)
C)
D)
A) is not defined.
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
78
Solve the problem.
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
79
Find the product AB, if possible.
A)
B) is not defined.
C)
D)
A)
B) is not defined.
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
80
Solve the matrix equation for X.
Let and
A)
B)
C)
D)
Let and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck


