Exam 6: Matrices and Determinants

Find the products AB and BA to determine whether B is the multiplicative inverse of A. - $A = \left[ \begin{array} { l l } 5 & 3 \\3 & 2\end{array} \right] , \quad B = \left[ \begin{array} { r r } 2 & - 3 \\- 3 & 5\end{array} \right]$

Evaluate the determinant. - $\left| \begin{array} { r r } 1 & 1 \\ - 6 & - 4 \end{array} \right|$

Solve the problem. -The area of a triangle with vertices $\left( x _ { 1 } , y _ { 1 } \right) , \left( x _ { 2 } , y _ { 2 } \right)$ , and $\left( x _ { 3 } , y _ { 3 } \right)$ is $\text { Area } = \pm \frac { 1 } { 2 } \left| \begin{array} { l l l } x _ { 1 } & y _ { 1 } & 1 \\x _ { 2 } & y _ { 2 } & 1 \\x _ { 3 } & y _ { 3 } & 1\end{array} \right|$ where the symbol $\pm$ indicates that the appropriate sign should be chosen to yield a positive area. Use this formula to find the area of a triangle whose vertices are $( 2,10 ) , ( 6 , - 4 )$ , and $( - 3 , - 9 )$ .

Solve the problem. -Let $A = \left[ \begin{array} { l l } - 1 & 2 \end{array} \right]$ and $B = \left[ \begin{array} { l l } 1 & 0 \end{array} \right]$ . Find $2 A + 3 B$ .

Find the products AB and BA to determine whether B is the multiplicative inverse of A. - $A = \left[ \begin{array} { r r } 4 & - 2 \\- 6 & 2\end{array} \right]$

Solve the problem. -Let $A = \left[ \begin{array} { r r } - 7 & 1 \\ 2 & 5 \end{array} \right]$ and $B = \left[ \begin{array} { r r } 6 & 2 \\ 3 & - 3 \end{array} \right]$ . Find $A + B$ .

Write a system of linear equations in three variables, and then use matrices to solve the system. -The table below shows the number of birds for three selected years after an endangered species protection program was started. 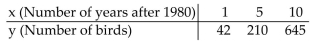Use the quadratic function $y = a x ^ { 2 } + b x + c$ to model the data. Solve the system of linear equations involving $a , b$ , and $c$ using matrices. Find the equation that models the data.

Find the products AB and BA to determine whether B is the multiplicative inverse of A. - $A = \left[ \begin{array} { r r } - 2 & 4 \\4 & - 4\end{array} \right] , \quad B = \left[ \begin{array} { l } \frac { 1 } { 2 } \frac { 1 } { 4 } \\\frac { 1 } { 2 } \frac { 1 } { 4 }\end{array} \right]$

Apply Gaussian Elimination to Systems with More Variables than Equations Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists. - 2x+y+2z-4w =10 x+3y+2z-11w =17 3x+y+7z-21w =0

Model Applied Situations with Matrix Operations The $\perp$ shape in the figure below is shown using 9 pixels in a $3 \times 3$ grid. The color levels are given to the right of the figure. Use the matrix $\left[ \begin{array} { l l l } 1 & 3 & 1 \\ 1 & 3 & 1 \\ 3 & 3 & 3 \end{array} \right]$ that represents a digital photograph of the $\perp$ shape to solve the problem. -Adjust the contrast by leaving the black alone and changing the light grey to dark grey. Use matrix addition to accomplish this.

Solve the problem. -Let $A = \left[ \begin{array} { r r } - 1 & 0 \\ 5 & 3 \end{array} \right]$ and $B = \left[ \begin{array} { r r } - 1 & 5 \\ 3 & 1 \end{array} \right]$ . Find $A - B$ .

Write the augmented matrix for the system of equations. - x-5y+z=11 y+7z=19 z=15

Find the products AB and BA to determine whether B is the multiplicative inverse of A. - $A = \left[ \begin{array} { r r r } 1 & 0 & 0 \\- 1 & 1 & 0 \\0 & - 6 & 1\end{array} \right]$

Find the products AB and BA to determine whether B is the multiplicative inverse of A. - $A = \left[ \begin{array} { l l } 10 & 1 \\- 1 & 0\end{array} \right] , \quad B = \left[ \begin{array} { r r } 0 & 1 \\- 1 & 10\end{array} \right]$

Apply Gaussian Elimination to Systems Without Unique Solutions Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists. - 4x-y+3z=12 x+4y+6z=-32 5x+3y+9z=20

Use Cramer's rule to solve the system. - 4x+3y-z=31 x-3y+2z=-5 4x+y+z=29

Solve the problem. -Let $A = \left[ \begin{array} { r r } - 6 & 6 \\ - 1 & - 5 \\ 6 & - 8 \end{array} \right]$ and $B = \left[ \begin{array} { r r } 2 & - 5 \\ - 3 & - 9 \\ - 6 & 6 \end{array} \right]$ . Find $A + B$ .

Apply Gaussian Elimination to Systems Without Unique Solutions Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists. - 5x+2y+z=-11 2x-3y-z=17 7x-y=12

Solve the problem. -Let $A = \left[ \begin{array} { r } 1 \\ - 3 \\ 2 \end{array} \right]$ and $B = \left[ \begin{array} { r } - 1 \\ 3 \\ - 2 \end{array} \right]$ . Find $A - 2 B$

Use Matrices and Gaussian Elimination to Solve Systems Solve the system of equations using matrices. Use Gaussian elimination with back-substitution. - x+y+z-w =6 2x-y+3z+4w =-4 4x+2y-z-w =-13 -x-2y+4z+3w= 12