Deck 11: The Analysis of Variance
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/156
Play
Full screen (f)
Deck 11: The Analysis of Variance
1
When the effect of a level for one factor depends on which level of another factor is present, the most appropriate ANOVA design to use in this situation is the:
A) one-way ANOVA
B) two-way ANOVA
C) three-way ANOVA
D) randomized block design
E) matched pairs design
A) one-way ANOVA
B) two-way ANOVA
C) three-way ANOVA
D) randomized block design
E) matched pairs design
two-way ANOVA
2
In a two-way factor ANOVA, the smallest number of replications required in any cell is 2, but all cells must have the same number of replications.
True
3
In a two-way factor ANOVA with replications, the null hypothesis for testing whether interaction exists is that no interaction exists, while the alternative hypothesis is that interaction does exist.
True
4
The number of cells in a two-way factor ANOVA is equal to a + b  1; where a is the number of levels of factor A and b is the number of levels of factor B.
1; where a is the number of levels of factor A and b is the number of levels of factor B.
 1; where a is the number of levels of factor A and b is the number of levels of factor B.
1; where a is the number of levels of factor A and b is the number of levels of factor B.
Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
5
In order to conduct a two-way factor ANOVA with replications, the number of replications r must be the same in each cell.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
6
In the two-way ANOVA where a is the number of factor A levels, b in the number of factor B levels, and r in the number of replicates, the number of degrees of freedom for error is:
A) (a1)(b1)
B) abr1
C) (a1)(r1)
D) ab(r1)
E) (a + 1)(r + 1)
A) (a1)(b1)
B) abr1
C) (a1)(r1)
D) ab(r1)
E) (a + 1)(r + 1)

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
7
In a two-way factor ANOVA, the total sum of squares can be partitioned into four parts: the variation due to factor A, the variation due to factor B, the error variation, and the variation due to blocking.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
8
In the 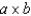 factorial experiment, where a is the number of levels for factor A, b is the number of levels for factor B, and r in the number of replications of each of the ab factor combinations, the degrees of freedom for interaction is given by:
factorial experiment, where a is the number of levels for factor A, b is the number of levels for factor B, and r in the number of replications of each of the ab factor combinations, the degrees of freedom for interaction is given by:
A) (a1)(b1)
B) (a1)(r1)
C) (b1)(r1)
D) ab(r1)
E) (b + 1)(r + 1)
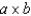 factorial experiment, where a is the number of levels for factor A, b is the number of levels for factor B, and r in the number of replications of each of the ab factor combinations, the degrees of freedom for interaction is given by:
factorial experiment, where a is the number of levels for factor A, b is the number of levels for factor B, and r in the number of replications of each of the ab factor combinations, the degrees of freedom for interaction is given by:A) (a1)(b1)
B) (a1)(r1)
C) (b1)(r1)
D) ab(r1)
E) (b + 1)(r + 1)

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
9
In a two-way factor ANOVA, the variances of the populations are assumed to be equal unless the error variation is zero.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
10
In a two-way ANOVA, it is easier to interpret main effects when the interaction component is not significant.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
11
A complete 3 x 2 factorial experiment is called balanced if:
A) factor A has three levels
B) factor B has two levels
C) the number of replicates is the same for each treatment
D) the number of observations for each combination of factor A and factor B levels equal at least 5
E) none of these
A) factor A has three levels
B) factor B has two levels
C) the number of replicates is the same for each treatment
D) the number of observations for each combination of factor A and factor B levels equal at least 5
E) none of these

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
12
Interaction in an experimental design can be tested in:
A) a completely randomized model
B) a randomized block model
C) a two-way factor model
D) all ANOVA models
E) none of these
A) a completely randomized model
B) a randomized block model
C) a two-way factor model
D) all ANOVA models
E) none of these

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
13
In a two-way factor ANOVA, the sum of squares due to both factors, the interaction sum of squares, and the error sum of squares must add up to the total sum of squares.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
14
In a two-way factor ANOVA with replications in which all hypotheses are to be tested at the .05 significance level, if the p-value for interaction is .0257, then we should conclude that no interaction exists between the levels of the two factors.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
15
The equation: "Total SS = SSA + SSB + SS(AB) + SSE" applies to which ANOVA model?
A) one-way ANOVA
B) a two-factor factorial design
C) completely randomized design
D) randomized block design
E) none of these
A) one-way ANOVA
B) a two-factor factorial design
C) completely randomized design
D) randomized block design
E) none of these

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
16
A study will be undertaken to examine the effect of two kinds of background music and of two assembly methods on the output of workers at a fitness shoe factory. Two workers will be randomly assigned to each of four groups, for a total of eight in the study. Each worker will be given a headphone set so that the music type can be controlled. The number of shoes completed by each worker will be recorded. Does the kind of music or the assembly method or a combination of music and method affect output? The ANOVA model most likely to fit this situation is the two-way analysis of variance.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
17
In a two-way factor ANOVA with replications, the reason for separating out the sum of squares due to interaction between factors A and B is to increase the chance of detecting significant differences across levels of factor A and factor B.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
18
In ANOVA for an a 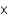 b factorial experiment, it is necessary to have at least two measurements at each level of each factor in order to analyze any interaction between the factors.
b factorial experiment, it is necessary to have at least two measurements at each level of each factor in order to analyze any interaction between the factors.
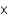 b factorial experiment, it is necessary to have at least two measurements at each level of each factor in order to analyze any interaction between the factors.
b factorial experiment, it is necessary to have at least two measurements at each level of each factor in order to analyze any interaction between the factors.
Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
19
In a two-way factor ANOVA, if factors A and B do not interact, then neither A nor B can be considered statistically significant.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
20
In a two-way ANOVA, there are 4 levels for factor A, 5 levels for factor B, and 3 observations for each combination of factor A and factor B levels. The number of treatments in this experiment equals:
A) 60
B) 25
C) 20
D) 16
E) 12
A) 60
B) 25
C) 20
D) 16
E) 12

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
21
In employing the randomized block design, the primary interest lies in reducing sum of squares for blocks (SSB).

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
22
In a two-way ANOVA, there are 4 levels for factor A, 3 levels for factor B, and 3 observations within each of the 12 factor combinations. The number of treatments in this experiment will be 36.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
23
A randomized block design ANOVA has two treatments. The test to be performed in this procedure is equivalent to dependent samples t-test.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
24
In a two-way ANOVA, where a is the number of factor A levels and b is the number of factor B levels, the number of the degrees of freedom for the "error term" is:
A) (a1)(b1)
B) nab
C) (a1) + (b1)
D) abn + 1
E) (a + 1)(b + 1)
A) (a1)(b1)
B) nab
C) (a1) + (b1)
D) abn + 1
E) (a + 1)(b + 1)

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
25
If we first arrange test units into similar groups before assigning treatments to them, the test design we should use is the randomized block design.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
26
When the problem objective is to compare more than two populations, the experimental design that is the counterpart of the matched pairs experiment is called the randomized block design.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
27
Three tennis players, a beginner, an experienced, and a professional, have been randomly selected from the membership of a large city tennis club. Using the same ball, each person hits four serves with each of five racquet models, with the five racquet models selected randomly. Each serve is clocked with a radar gun and the result recorded. Among ANOVA models, this setup is most like the randomized block design.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
28
Blocking is a procedure that lets extraneous factors operate during an experiment but assures - by virtue of the random selection of experimental units and their subsequent random assignment to experimental and control groups - that each treatment has an equal chance to be enhanced or handicapped by these factors.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
29
In a two-way ANOVA, there are 4 levels for factor A, 3 levels for factor B, and two observations within each of the 12 factor combinations. The number of treatments in this experiment will be 12.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
30
The purpose of designing a randomized block experiment is to reduce the between-treatments variation (SST) to more easily detect differences between the treatment means.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
31
The randomized block design is also called the two-way analysis of variance.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
32
The randomized block design is a two-way classification design.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
33
The randomized block design with two treatments is equivalent to a non-directional dependent samples z-test.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
34
A researcher at Michigan State University (MSU) wanted to determine whether different building signs (building maps versus wall signage) affect the total amount of time visitors require to reach their destination and whether that time depends on whether the starting location is inside or outside the building. Three subjects were assigned to each of the combinations of signs and starting locations, and travel time in seconds from beginning to destination was recorded. A partial computer output of the appropriate analysis is given below: 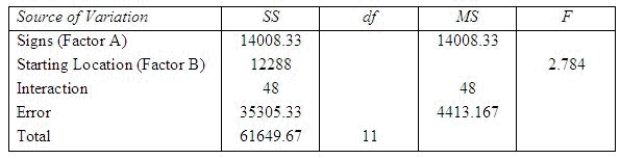 The degrees of freedom for the different building signs are ______________.
The degrees of freedom for the different building signs are ______________.
The degrees of freedom for the different starting location are ______________.
The degrees of freedom for the interaction between the levels of signs and starting location are ______________.
The error degrees of freedom are ______________.
The mean squares value for starting location is ______________.
The F test statistic for testing the main effect of types of signs is ______________.
The F test statistic for testing the interaction effect between the types of signs and the starting location is ______________.
In order to determine the critical value of the F ratio against which to test for differences between the levels of factor A, we should use numerator df = ______________, and denominator df = ______________.
In order to determine the critical value of the F ratio against which to test for differences between the levels of factor B, we should use numerator df = ______________, and denominator df = ______________.
In order to determine the critical value of the F ratio against which to test for interaction between levels of Factor A and levels of Factor B, we should use numerator df = ______________, and denominator of F = ______________.
 The degrees of freedom for the different building signs are ______________.
The degrees of freedom for the different building signs are ______________.The degrees of freedom for the different starting location are ______________.
The degrees of freedom for the interaction between the levels of signs and starting location are ______________.
The error degrees of freedom are ______________.
The mean squares value for starting location is ______________.
The F test statistic for testing the main effect of types of signs is ______________.
The F test statistic for testing the interaction effect between the types of signs and the starting location is ______________.
In order to determine the critical value of the F ratio against which to test for differences between the levels of factor A, we should use numerator df = ______________, and denominator df = ______________.
In order to determine the critical value of the F ratio against which to test for differences between the levels of factor B, we should use numerator df = ______________, and denominator df = ______________.
In order to determine the critical value of the F ratio against which to test for interaction between levels of Factor A and levels of Factor B, we should use numerator df = ______________, and denominator of F = ______________.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
35
The F-test of the randomized block design of the analysis of variance has the same requirements as the independent samples design; that is, the random variable must be normally distributed and the population variances must be equal.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
36
The completely randomized design is an experimental plan that divides all available experimental units into blocks of fairly homogeneous units - each block containing as many units as there are treatments or some multiple of that number - and then randomly matches each treatment with one or more units within each block.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
37
A randomized block experiment having five treatments and four blocks produced the following values: Total SS = 1500, SST = 275, SSE = 153. The value of MSB must be 268.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
38
A randomized block design ANOVA has five treatments and four blocks. The computed test statistic (value of F) is 6.25. With a 0.05 significance level, the conclusion will be to accept the null hypothesis.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
39
Two samples of ten each from the male and female workers of a large company have been taken. The data involved the wage rate of each worker. To test whether there is any difference in the average wage rate between male and female workers a pooled-variances t-test will be considered. Another test option to consider is ANOVA. The most likely ANOVA to fit this test situation is the randomized block design.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
40
In the analysis of variance, the sum of the squared deviations between each block sample mean and the grand mean, multiplied by the number of observations made for each block, multiplied by the number of observations per cell (which may well equal 1) equals the blocks mean square.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
41
Which of the following statements about blocks variation is false?
A) It equals the sum of the squared deviations between each block sample mean and the grand mean.
B) It measures the variation among block sample means, which is attributable not to chance to inherent differences among blocks of experimental units.
C) In two-way ANOVA, it equals the blocks mean square.
D) In three-way ANOVA, it equals the blocks sample mean.
E) None of these.
A) It equals the sum of the squared deviations between each block sample mean and the grand mean.
B) It measures the variation among block sample means, which is attributable not to chance to inherent differences among blocks of experimental units.
C) In two-way ANOVA, it equals the blocks mean square.
D) In three-way ANOVA, it equals the blocks sample mean.
E) None of these.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
42
A study was conducted to compare automobile gasoline mileage for three brands of gasoline, A, B, and C. Four automobiles, all of the same make and model, were used in the experiment, and each gasoline brand was tested in each automobile. Using each brand in the same automobile has the effect of eliminating (blocking out) automobile-to-automobile variability. The data (in miles per gallon) are as follows:  Use Minitab or Excel to generate a summary table and the ANOVA table.
Use Minitab or Excel to generate a summary table and the ANOVA table.
Do the data provide sufficient evidence to indicate a difference in mean mileage per gallon for the three brands of gasoline?
F = ______________
p-value = ______________
There ______________ sufficient evidence to indicate a difference in mean mileage per gallon for the three brands of gasoline.
Is there evidence of a difference in mean mileage for the four automobiles?
F = ______________
p-value = ______________
There ______________ sufficient evidence to indicate a difference in mean mileage per gallon for the four automobiles.
 Use Minitab or Excel to generate a summary table and the ANOVA table.
Use Minitab or Excel to generate a summary table and the ANOVA table.Do the data provide sufficient evidence to indicate a difference in mean mileage per gallon for the three brands of gasoline?
F = ______________
p-value = ______________
There ______________ sufficient evidence to indicate a difference in mean mileage per gallon for the three brands of gasoline.
Is there evidence of a difference in mean mileage for the four automobiles?
F = ______________
p-value = ______________
There ______________ sufficient evidence to indicate a difference in mean mileage per gallon for the four automobiles.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
43
A consumer was interested in determining whether there is a significant difference in the price charged for tools by three hardware stores. The consumer selected five tools and recorded the price for each tool in each store. The following data was recorded:  Fmodel = ______________
Fmodel = ______________
p-value = ______________
Ftool = ______________
p-value = ______________
Fstore = ______________
p-value = ______________
______________
 Fmodel = ______________
Fmodel = ______________p-value = ______________
Ftool = ______________
p-value = ______________
Fstore = ______________
p-value = ______________
______________

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
44
In a randomized block design of ANOVA, which of the following correctly describes the number of degrees of freedom associated with the sum of squares for treatments?
A) One less than the total number in observations in all samples.
B) One less than the number of blocks.
C) One less than the number of populations involved.
D) One more than the number of populations involved.
E) None of these.
A) One less than the total number in observations in all samples.
B) One less than the number of blocks.
C) One less than the number of populations involved.
D) One more than the number of populations involved.
E) None of these.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
45
The F-test of the randomized block design of the analysis of variance requires that the random variable of interest must be normally distributed and the population variances must be equal. When the random variable is not normally distributed, we can use:
A) one-way ANOVA
B) two-way ANOVA
C) chi-square test
D) binomial square test
E) Friedman test
A) one-way ANOVA
B) two-way ANOVA
C) chi-square test
D) binomial square test
E) Friedman test

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
46
The equation: "Total SS = SST + SSB + SSE" applies to which ANOVA model?
A) one-way ANOVA
B) a two-factor factorial design
C) completely randomized design
D) randomized block design
E) none of these
A) one-way ANOVA
B) a two-factor factorial design
C) completely randomized design
D) randomized block design
E) none of these

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
47
The randomized block design with exactly two treatments is equivalent to a two-tail:
A) independent samples z-test
B) independent samples equal-variances t-test
C) independent samples unequal-variances t-test
D) matched pairs t-test
E) independent samples t-test
A) independent samples z-test
B) independent samples equal-variances t-test
C) independent samples unequal-variances t-test
D) matched pairs t-test
E) independent samples t-test

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
48
In the randomized block design ANOVA, the sum of squares for error equals:
A) Total SSSST
B) Total SSSSB
C) Total SSSSTSSB
D) Total SSSS(A)
E) Total SSSS(A)SS(B)SS(AB)
A) Total SSSST
B) Total SSSSB
C) Total SSSSTSSB
D) Total SSSS(A)
E) Total SSSS(A)SS(B)SS(AB)

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
49
In a randomized block design of ANOVA, how many factors are there to be analyzed?
A) one factor
B) two factors
C) three factors
D) four or more factors
E) all of these
A) one factor
B) two factors
C) three factors
D) four or more factors
E) all of these

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
50
Three tennis players, a beginner, an intermediate, and advanced, have been randomly selected from the membership of a racquet facility club in a large city. Using the same tennis ball, each player hits ten serves, one with each of three racquet models, with the three racquet models selected randomly. The speed of each serve is measured with a machine and the result recorded. Among the ANOVA models listed below, the most likely model to fit this situation is the:
A) one-way ANOVA
B) two-way ANOVA
C) randomized block design
D) matched-pairs model
E) chi-square test
A) one-way ANOVA
B) two-way ANOVA
C) randomized block design
D) matched-pairs model
E) chi-square test

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
51
In the randomized block design for ANOVA, where k is the number of treatments and b in the number of blocks, the number of degrees of freedom for error is:
A) k1
B) b1
C) (k1)(b1)
D) kb1
E) kb + 1
A) k1
B) b1
C) (k1)(b1)
D) kb1
E) kb + 1

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
52
An analysis of variance that controls extraneous factors by using the randomized block design is called:
A) one-way ANOVA
B) two-way ANOVA
C) three-way ANOVA
D) four-way ANOVA
E) five-way ANOVA
A) one-way ANOVA
B) two-way ANOVA
C) three-way ANOVA
D) four-way ANOVA
E) five-way ANOVA

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
53
A company conducted an experiment to determine the effect of two types of incentive pay plans on worker productivity for workers of two shifts. The company used an equal number of production workers from each of the two shifts and one-half of these workers were assigned to each plan. Then five workers from each pay plan-shift combination were selected and their productivity (in number of items produced) recorded for a one week period. The following output was generated using Minitab: 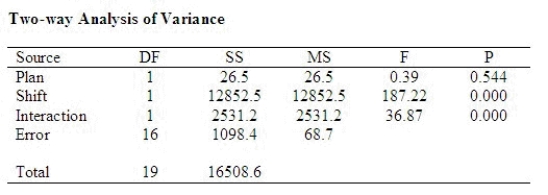 Is there significant interaction present in this problem? Let
Is there significant interaction present in this problem? Let 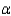 = 0.05.
= 0.05.
The p-value ______________ indicate significant interaction.
Based on the previous answer, is testing for the main effects, plan and shift, appropriate?
________________________________________________________
 Is there significant interaction present in this problem? Let
Is there significant interaction present in this problem? Let 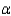 = 0.05.
= 0.05.The p-value ______________ indicate significant interaction.
Based on the previous answer, is testing for the main effects, plan and shift, appropriate?
________________________________________________________

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
54
The equation: SS(Total) = SST + SSB + SSE, applies to which ANOVA model?
A) one-way ANOVA
B) two-way ANOVA
C) completely randomized design
D) randomized block design
E) none of these
A) one-way ANOVA
B) two-way ANOVA
C) completely randomized design
D) randomized block design
E) none of these

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
55
A randomized block design with 4 treatments and 5 blocks produced the following sum of squares values: Total SS = 1951, SST = 349, SSE = 188. The value of SSB must be:
A) 1414
B) 537
C) 1763
D) 1602
E) 1312
A) 1414
B) 537
C) 1763
D) 1602
E) 1312

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
56
The primary interest of designing a randomized block experiment is to:
A) reduce the variation among blocks
B) increase the between-treatments variation to more easily detect differences among the treatment means
C) reduce the within-treatments variation to more easily detect differences among the treatment means
D) increase the total sum of squares
E) none of these
A) reduce the variation among blocks
B) increase the between-treatments variation to more easily detect differences among the treatment means
C) reduce the within-treatments variation to more easily detect differences among the treatment means
D) increase the total sum of squares
E) none of these

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
57
In the randomized block design for ANOVA where k is the number of treatments and b in the number of blocks, the degrees of freedom for error is given by:
A) bk1
B) kb + 1
C) (b1)(k1)
D) k + b1
E) (b + 1)(k + 1)
A) bk1
B) kb + 1
C) (b1)(k1)
D) k + b1
E) (b + 1)(k + 1)

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
58
A randomized block design with 4 treatments and 5 blocks produced the following sum of squares values: SS(Total) = 2000, SST = 400, SSE = 200. The value of MSB must be 350.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
59
An avid runner was interested in whether there is a significant difference in the average wear (measured in weeks of use) among three brands of running shoes. To answer the question, the runner randomly selected six runners and assigned them to wear each of the three brands of running shoes until the shoes wore out. Each of the runners wore the brands of shoes in a random order. After the data had been recorded, the following output was generated using Minitab: 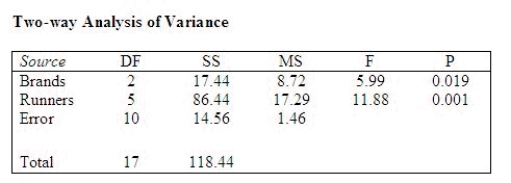 What are the blocks?
What are the blocks?
______________
What are the treatments?
______________
The p-value ______________ indicate significant results.
Is blocking necessary in this problem?
______________
Justify your answer.
________________________________________________________
Use the p-value approach to determine whether there is a significant difference in the average wear between the three brands of running shoes. Let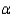 = 0.05.
= 0.05.
The p-value ______________ indicate significant results.
______________ of the brands of running shoes has a significantly different average wear than the others.
 What are the blocks?
What are the blocks?______________
What are the treatments?
______________
The p-value ______________ indicate significant results.
Is blocking necessary in this problem?
______________
Justify your answer.
________________________________________________________
Use the p-value approach to determine whether there is a significant difference in the average wear between the three brands of running shoes. Let
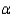 = 0.05.
= 0.05.The p-value ______________ indicate significant results.
______________ of the brands of running shoes has a significantly different average wear than the others.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
60
In a randomized block design of ANOVA, which of the following statements is true?
A) The sum of squares for treatments (SST) measures the variation among the treatment means.
B) The sum of squares for blocks (SSB) measures the variation among the block means.
C) The sum of squares for error (SSE) measures the variation of the differences among the treatment observations within blocks.
D) All of these.
E) None of these.
A) The sum of squares for treatments (SST) measures the variation among the treatment means.
B) The sum of squares for blocks (SSB) measures the variation among the block means.
C) The sum of squares for error (SSE) measures the variation of the differences among the treatment observations within blocks.
D) All of these.
E) None of these.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
61
Tukey's method for paired comparisons assumes that the sample means are equal and independent of each other.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
62
Tukey's method for paired comparisons makes the probability of declaring that a difference exists between at least one pair in a set of k treatments, when no difference exists, equal to 1 - 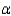 .
.
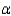 .
.
Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
63
Given the significance level 0.05, the F-value for the degrees of freedom 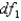 =5 and
=5 and 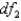 = 8, is 4.82.
= 8, is 4.82.
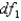 =5 and
=5 and 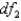 = 8, is 4.82.
= 8, is 4.82.
Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
64
One of the assumptions underlying analysis of variance for a completely randomized design is that the observations within each population are normally distributed with unequal variance.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
65
The studentized range is the difference between the smallest and the largest in a set of k samples means. It is used for determining whether there is a difference in a pair of population means.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
66
In analysis of variances, the sum of squares for treatments (SST) is zero when all the sample means are equal.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
67
Analysis of variance (ANOVA) is a procedure for comparing more than two population means.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
68
An independent random sampling design was used to compare the means of six treatments based on samples of four observations per treatment. The pooled estimator of 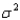 is 9.42, and the sample means follow:
is 9.42, and the sample means follow: 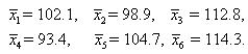 Give the value of
Give the value of 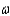 that you would use to make pairwise comparisons of the treatment means for
that you would use to make pairwise comparisons of the treatment means for 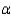 = 0.05. Rank the treatment means using pairwise comparisons.
= 0.05. Rank the treatment means using pairwise comparisons.
Test statistics = ______________
Rank the treatment means using pairwise comparisons. Enter just the subscripts in order (1, 4, etc.).
_____ _____ _____ _____ _____ _____
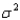 is 9.42, and the sample means follow:
is 9.42, and the sample means follow: 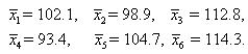 Give the value of
Give the value of 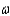 that you would use to make pairwise comparisons of the treatment means for
that you would use to make pairwise comparisons of the treatment means for 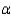 = 0.05. Rank the treatment means using pairwise comparisons.
= 0.05. Rank the treatment means using pairwise comparisons.Test statistics = ______________
Rank the treatment means using pairwise comparisons. Enter just the subscripts in order (1, 4, etc.).
_____ _____ _____ _____ _____ _____

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
69
Which of the following correctly describes Tukey's method of paired comparisons?
A) It is a statistical technique designed to test whether the means of more than two quantitative populations are equal.
B) It is a method employed as a follow-up to ANOVA that seeks out "honestly significant differences" between paired sample means.
C) It is a method to determine whether different statistical populations having equal variances.
D) It is a method to measure a statistical test's sensitivity to any breach of ANOVA basic assumptions.
E) None of these.
A) It is a statistical technique designed to test whether the means of more than two quantitative populations are equal.
B) It is a method employed as a follow-up to ANOVA that seeks out "honestly significant differences" between paired sample means.
C) It is a method to determine whether different statistical populations having equal variances.
D) It is a method to measure a statistical test's sensitivity to any breach of ANOVA basic assumptions.
E) None of these.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
70
The analysis of variance (ANOVA) technique analyzes the variance of the data to determine whether differences exist between the population variances.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
71
Multiple comparison methods are used in one-way ANOVA and if the null hypothesis states that there is no difference between the treatment means, the null hypothesis is:
A) rejected
B) accepted
C) equal to zero
D) either rejected or accepted
E) neither rejected nor accepted
A) rejected
B) accepted
C) equal to zero
D) either rejected or accepted
E) neither rejected nor accepted

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
72
Which of the following is not true of Tukey's Multiple Comparison Method?
A) It is based on the studentized range statistic q to obtain the critical value needed to construct individual confidence intervals.
B) It requires that all sample sizes are equal, or at least similar.
C) It can be employed instead of the analysis of variance.
D) All of these.
E) None of these.
A) It is based on the studentized range statistic q to obtain the critical value needed to construct individual confidence intervals.
B) It requires that all sample sizes are equal, or at least similar.
C) It can be employed instead of the analysis of variance.
D) All of these.
E) None of these.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
73
The equation: Total SS = SST + SSB + SSE, applies to the completely randomized design (one-way ANOVA model).

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
74
Tukey's multiple comparison method determines a critical number, 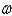 , such that if any pair of sample means has a difference greater than
, such that if any pair of sample means has a difference greater than 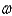 , we conclude that the pair's two corresponding population means are different.
, we conclude that the pair's two corresponding population means are different.
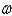 , such that if any pair of sample means has a difference greater than
, such that if any pair of sample means has a difference greater than 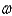 , we conclude that the pair's two corresponding population means are different.
, we conclude that the pair's two corresponding population means are different.
Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
75
The data that follow are observations collected from an experiment that compared four treatments, A, B, C, and D, within each of three blocks, using a randomized block design.  Rank the four treatment means using Tukey's method of paired comparisons with
Rank the four treatment means using Tukey's method of paired comparisons with 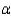 = 0.01.
= 0.01.
Ranked means (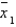 is the smallest,
is the smallest, 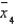 is the largest).
is the largest). 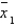 = ______________
= ______________ 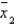 = ______________
= ______________ 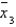 = ______________
= ______________ 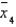 = ______________
= ______________
Conclusion: ______________
 Rank the four treatment means using Tukey's method of paired comparisons with
Rank the four treatment means using Tukey's method of paired comparisons with 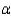 = 0.01.
= 0.01.Ranked means (
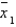 is the smallest,
is the smallest, 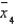 is the largest).
is the largest). 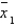 = ______________
= ______________ 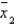 = ______________
= ______________ 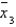 = ______________
= ______________ 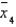 = ______________
= ______________Conclusion: ______________

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
76
Tukey's method for making paired comparisons is based on the usual ANOVA assumptions.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
77
A building contractor employs three construction engineers, A, B, and C to estimate and bid on jobs. To determine whether one tends to be a more conservative (or liberal) estimator than the others, the contractor selects four projected construction jobs and has each estimator independently estimate the cost (in dollars per square foot) of each job. The data are shown in the table:  Analyze the experiment using the appropriate methods.
Analyze the experiment using the appropriate methods.
Means Plot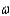 = ______________
= ______________
There ______________ differences between that group of means.
 Analyze the experiment using the appropriate methods.
Analyze the experiment using the appropriate methods.Means Plot
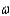 = ______________
= ______________There ______________ differences between that group of means.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
78
Tukey's multiple comparison method determines a critical number 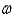 , such that, if any pair of sample means has a difference smaller than this critical number, we conclude that the pair's two corresponding population means are different.
, such that, if any pair of sample means has a difference smaller than this critical number, we conclude that the pair's two corresponding population means are different.
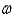 , such that, if any pair of sample means has a difference smaller than this critical number, we conclude that the pair's two corresponding population means are different.
, such that, if any pair of sample means has a difference smaller than this critical number, we conclude that the pair's two corresponding population means are different.
Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
79
In analysis of variances, the sum of squares for error (SSE) is zero when all the sample variances are equal.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck
80
Why would you use the Tukey multiple comparison?
A) To test for normality.
B) To test for homogeneity of variance.
C) To test independence of errors.
D) To test for differences in pairwise means.
E) To test for differences in sample population means.
A) To test for normality.
B) To test for homogeneity of variance.
C) To test independence of errors.
D) To test for differences in pairwise means.
E) To test for differences in sample population means.

Unlock Deck
Unlock for access to all 156 flashcards in this deck.
Unlock Deck
k this deck


