Deck 4: Probability and Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/136
Play
Full screen (f)
Deck 4: Probability and Probability Distributions
1
There are two types of random variables: discrete and continuous.
True
2
The number of homes sold by a real estate agency in a three week period is an example of a continuous random variable.
False
3
The probability distribution of the number of accidents in Grand Rapids, Michigan, each day is given by  Based on this distribution, the standard deviation of the number of accidents per day is approximately:
Based on this distribution, the standard deviation of the number of accidents per day is approximately:
Round your answer to two decimal places.
A) 6.95
B) 2.33
C) 2.64
D) 1.53
E) 15
 Based on this distribution, the standard deviation of the number of accidents per day is approximately:
Based on this distribution, the standard deviation of the number of accidents per day is approximately:Round your answer to two decimal places.
A) 6.95
B) 2.33
C) 2.64
D) 1.53
E) 15
1.53
4
A random variable is any variable the numerical value of which is determined by a random experiment, and, thus, by chance.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
5
The expected number of heads in 500 tosses of an unbiased coin is:
A) 150
B) 200
C) 250
D) 300
E) 500
A) 150
B) 200
C) 250
D) 300
E) 500

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
6
Which of following statements is true regarding the probability distribution for a discrete random variable X?
A) The probabilities must be nonnegative.
B) The probabilities must sum to 1.
C) The random variable must take on positive values between 0 and 1.
D) Both the probabilities must be nonnegative and the probabilities must sum to 1.
E) Both the probabilities must be nonnegative and the random variable must take on positive values between 0 and 1.
A) The probabilities must be nonnegative.
B) The probabilities must sum to 1.
C) The random variable must take on positive values between 0 and 1.
D) Both the probabilities must be nonnegative and the probabilities must sum to 1.
E) Both the probabilities must be nonnegative and the random variable must take on positive values between 0 and 1.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
7
The number of students living off-campus is an example of a discrete random variable.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
8
The weight of a box of candy bars is an example of a discrete random variable since there are only a specific number of bars in the box.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
9
The mean of a discrete random variable x:
A) is denoted by
B) is denoted by E(x), because it is the value of x one can expect to find on average by numerous repetitions of the random experiment that generates the variable's actual values
C) is correctly described by both "is denoted by" and "is denoted by E(x), because it is the value of x one can expect to find on average by numerous repetitions of the random experiment that generates the variable's actual values"
D) is always = 0
E) is none of these
A) is denoted by
B) is denoted by E(x), because it is the value of x one can expect to find on average by numerous repetitions of the random experiment that generates the variable's actual values
C) is correctly described by both "is denoted by" and "is denoted by E(x), because it is the value of x one can expect to find on average by numerous repetitions of the random experiment that generates the variable's actual values"
D) is always = 0
E) is none of these

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
10
If the mean of the random variable x is larger than the mean of the random variable y, then the variance of x must be larger than the variance of y.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
11
A table, graph, or formula that associates each possible value of a discrete random variable, x with its probability of occurrence, p(x), is called a discrete probability distribution.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
12
In a set of all possible values a discrete random variable is countable, because the variable can assume values only at specific points on a scale of values, with inevitable gaps in-between.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
13
Which of the following correctly describes the nature of discrete quantitative variables?
A) They are characteristics possessed by persons or objects, called elementary units, in which we are interested.
B) They can assume values only at specific points on a scale of values, with inevitable gaps between successive observations
C) When dealing with such variables, we can count all possible observations and, with some exceptions, that count leads to a finite result.
D) Is correctly described by "they are characteristics possessed by persons or objects, called elementary units, in which we are interested" and "when dealing with such variables, we can count all possible observations and, with some exceptions, that count leads to a finite result."
E) All of these.
A) They are characteristics possessed by persons or objects, called elementary units, in which we are interested.
B) They can assume values only at specific points on a scale of values, with inevitable gaps between successive observations
C) When dealing with such variables, we can count all possible observations and, with some exceptions, that count leads to a finite result.
D) Is correctly described by "they are characteristics possessed by persons or objects, called elementary units, in which we are interested" and "when dealing with such variables, we can count all possible observations and, with some exceptions, that count leads to a finite result."
E) All of these.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
14
The probability distribution for a discrete variable x is a formula, a table, or a graph providing p(x), the probability associated with each of the values of x.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
15
The time required to assemble a computer is an example of a discrete random variable.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
16
If x is a discrete random variable, then x can take on only one of two possible values.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
17
The graph of a discrete random variable looks like a histogram where the probability of each possible outcome is represented by a bar.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
18
The probability distribution of the number of accidents in Grand Rapids, Michigan, each day is given by  This distribution is an example of:
This distribution is an example of:
A) continuous probability distribution
B) discrete probability distribution
C) conditional probability distribution
D) an expected value distribution
E) Is not a probability distribution.
 This distribution is an example of:
This distribution is an example of:A) continuous probability distribution
B) discrete probability distribution
C) conditional probability distribution
D) an expected value distribution
E) Is not a probability distribution.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
19
A table, formula, or graph that shows all possible values x a random variable can assume, together with their associated probabilities P(x) is called:
A) a discrete probability distribution
B) a continuous probability distribution
C) a bivariate probability distribution
D) a law of total probability
E) all of these
A) a discrete probability distribution
B) a continuous probability distribution
C) a bivariate probability distribution
D) a law of total probability
E) all of these

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
20
The probability distribution of the number of accidents in Grand Rapids, Michigan, each day is given by  Based on this distribution, the expected number of accidents in a given day is:
Based on this distribution, the expected number of accidents in a given day is:
A) 4.62
B) 1.47
C) 2.15
D) 1.81
E) 1
 Based on this distribution, the expected number of accidents in a given day is:
Based on this distribution, the expected number of accidents in a given day is:A) 4.62
B) 1.47
C) 2.15
D) 1.81
E) 1

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
21
A false negative in screening tests is the event that the test is positive for a given condition, given that the person does not have the condition.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
22
A false positive in screening (e.g., home pregnancy tests) represents the event that:
A) the test is negative for a given condition, given that the person does not have the condition
B) the test is positive for a given condition, given that the person does not have the condition
C) the test is negative for a given condition, given that the person has the condition
D) the test is positive for a given condition, given that the person has the condition
A) the test is negative for a given condition, given that the person does not have the condition
B) the test is positive for a given condition, given that the person does not have the condition
C) the test is negative for a given condition, given that the person has the condition
D) the test is positive for a given condition, given that the person has the condition

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
23
Let x be a random variable with the following distribution:
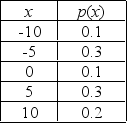 Round your answer to three decimal places, if necessary.
Round your answer to three decimal places, if necessary.
a. Find the expected value of x.
______________
b. Find the standard deviation of x.
______________
c. What is the probability that x is further than one standard deviation from the mean?
______________
 Round your answer to three decimal places, if necessary.
Round your answer to three decimal places, if necessary. a. Find the expected value of x.
______________
b. Find the standard deviation of x.
______________
c. What is the probability that x is further than one standard deviation from the mean?
______________

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
24
A false positive in screening tests is the event that the test is negative for a given condition, given that the person has the condition.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
25
From experience, a shipping company knows that the cost of delivering a small package within 24 hours is $16.20. The company charges $16.95 for shipment but guarantees to refund the charge if delivery is not made within 24 hours. If the company fails to deliver only 3% of its packages within the 24-hour period, what is the expected gain per package?
______________
______________

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
26
A false negative in screening tests (e.g., Steroid testing of athletes) represents the event that:
A) the test is negative for a given condition, given that the person does not have the condition
B) the test is positive for a given condition, given that the person does not have the condition
C) the test is negative for a given condition, given that the person has the condition
D) the test is positive for a given condition, given that the person has the condition
A) the test is negative for a given condition, given that the person does not have the condition
B) the test is positive for a given condition, given that the person does not have the condition
C) the test is negative for a given condition, given that the person has the condition
D) the test is positive for a given condition, given that the person has the condition

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
27
Which of the following statements is false?
A) The mean of a discrete probability distribution is equal to the square root of the variance.
B) The expected value of a discrete probability distribution is the long-run average value if the experiment is to be repeated many times.
C) The standard deviation of a discrete probability distribution measures the average variation of the random variable from the mean.
D) All of the above.
E) None of these.
A) The mean of a discrete probability distribution is equal to the square root of the variance.
B) The expected value of a discrete probability distribution is the long-run average value if the experiment is to be repeated many times.
C) The standard deviation of a discrete probability distribution measures the average variation of the random variable from the mean.
D) All of the above.
E) None of these.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
28
Approximately 5% of the bolts coming off a production line have serious defects. Two bolts are randomly selected for inspection. Find the probability distribution for x, the number of defective bolts in the sample.
a. P(x = 0) = P(both bolts are not defective)
______________
b. P(x = 1) = P(one bolt is defective)
______________
c. P(x = 2) = P(both bolts are defective)
______________
d. Find E(x).
______________
e. Find
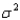 .
.
______________
a. P(x = 0) = P(both bolts are not defective)
______________
b. P(x = 1) = P(one bolt is defective)
______________
c. P(x = 2) = P(both bolts are defective)
______________
d. Find E(x).
______________
e. Find
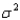 .
.______________

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
29
Steve takes either a bus or the subway to go to work with probabilities 0.25 and 0.75, respectively. When he takes the bus, he is late 40% of the days. When he takes the subway, he is late 30% of the days. If Steve is late for work on a particular day, what is the probability that he took the bus?
______________
______________

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
30
The random variable x is defined as the number of mistakes made by a typist on a randomly chosen page of a physics thesis. The probability distribution follows.
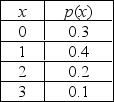 Round your answer to four decimal places, if necessary.
Round your answer to four decimal places, if necessary.
a. What is E(x)?
______________
b. Find
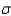 .
.
______________
c. Find P(x < 1).
______________
d. Find
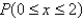 .
.
______________
e. In what fraction of pages in the thesis would the number of mistakes made be within two standard deviations of the mean?
______________
 Round your answer to four decimal places, if necessary.
Round your answer to four decimal places, if necessary. a. What is E(x)?
______________
b. Find
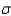 .
.______________
c. Find P(x < 1).
______________
d. Find
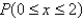 .
.______________
e. In what fraction of pages in the thesis would the number of mistakes made be within two standard deviations of the mean?
______________

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
31
Medical case histories indicate that different illnesses may produce identical symptom. Suppose a particular set of symptoms, which we will denote as event H, occurs only when any one of these illnesses: A, B, or C occurs. (For the sake of simplicity, we will assume that illnesses A, B, and C are mutually exclusive.) Studies show these probabilities of getting the three illnesses: 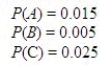 The probabilities of developing the symptoms H, given a specific illness, are:
The probabilities of developing the symptoms H, given a specific illness, are: 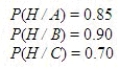 Assuming that an ill person shows the symptoms H, what is the probability that the person has illness A?
Assuming that an ill person shows the symptoms H, what is the probability that the person has illness A?
Round your answer to four decimal places.
______________
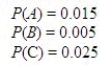 The probabilities of developing the symptoms H, given a specific illness, are:
The probabilities of developing the symptoms H, given a specific illness, are: 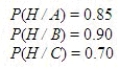 Assuming that an ill person shows the symptoms H, what is the probability that the person has illness A?
Assuming that an ill person shows the symptoms H, what is the probability that the person has illness A?Round your answer to four decimal places.
______________

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
32
Bayes' Rule is a formula for revising an initial subjective (prior) probability value on the basis of results obtained by an empirical investigation and for, thus, obtaining a new (posterior) probability value.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
33
In the "Quick Draw" casino card game, a player chooses one card from a deck of 52 well-shuffled cards. If the card the player selects is the king of hearts, the player wins $104; if the card is an ace, the player wins $78; if the card selected is anything else, the player loses $13. Considering a negative amount won to be a loss, how much should the player expect to win in one play of "Quick Draw"?
$ ______________
$ ______________

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
34
Screening tests (e.g., AIDS testing) are evaluated on the probability of a false negative or a false positive, and both of these are:
A) conditional probabilities
B) probability of the intersection of two events
C) probability of the union of two events
D) marginal probabilities
E) probability of dependent events
A) conditional probabilities
B) probability of the intersection of two events
C) probability of the union of two events
D) marginal probabilities
E) probability of dependent events

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
35
The neighborhood deli specializes in New York Style Cheesecake. The cheesecakes are made fresh daily and any unsold cheesecake is donated to the Salvation Army soup kitchen to feed the homeless. Each cheesecake costs $5 to make and sells for $11. The daily demand for cheesecake (the number the deli could sell if they had a cheesecake for everyone who wanted one) has the following distribution.
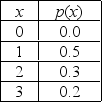
a. What is the expected demand for cheesecake?
______________
b. What is the expected daily profit if the deli makes only one cheesecake per day?
$ ______________
c. What is the expected daily profit if the deli makes only two cheesecakes per day?
$ ______________

a. What is the expected demand for cheesecake?
______________
b. What is the expected daily profit if the deli makes only one cheesecake per day?
$ ______________
c. What is the expected daily profit if the deli makes only two cheesecakes per day?
$ ______________

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
36
A sample is selected from one of two populations, S1 and S2, with probabilities P(S1) = 0.80 and P(S2) = 0.20. If the sample has been selected from S1, the probability of observing an event A is P(A / S1) = 0.15. Similarly, If the sample has been selected from S2, the probability of observing A is P(A / S2) = 0.25.
Round your answer to four decimal places, if necessary
a. If a sample is randomly selected from one of the two populations, what is the probability that event A occurs?
______________
If a sample is randomly selected and event A is observed, what is the probability that the sample was selected:
b. From population S1?
______________
c. From population S2?
______________
Round your answer to four decimal places, if necessary
a. If a sample is randomly selected from one of the two populations, what is the probability that event A occurs?
______________
If a sample is randomly selected and event A is observed, what is the probability that the sample was selected:
b. From population S1?
______________
c. From population S2?
______________

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
37
Let the random variable x represent the number of cars owned by a family. Assume that x can take on five values: 0, 1, 2, 3, 4. A partial probability distribution is shown below:

a. Find the probability that a family owns three cars.
______________
b. Find the probability that a family owns between 1 and 3 cars, inclusive.
______________
c. Find the probability that a family owns no more than one car.
______________
d. What is the probability that a family owns more than two cars?
______________
e. What is the probability that a family owns at most 3 cars?
______________

a. Find the probability that a family owns three cars.
______________
b. Find the probability that a family owns between 1 and 3 cars, inclusive.
______________
c. Find the probability that a family owns no more than one car.
______________
d. What is the probability that a family owns more than two cars?
______________
e. What is the probability that a family owns at most 3 cars?
______________

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
38
The probability distribution of your winnings at a casino's card game is shown below.
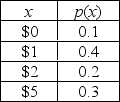
a. What is the chance you win more than $1 if you play just once?
______________
b. How much should you expect to win if you play the game once?
______________
c. After breaking the bank at the casino playing this card game, you decide to open your own casino where the customers can play your favorite card game. How much should you charge the players if you want to have an average profit of $1 per play?
______________

a. What is the chance you win more than $1 if you play just once?
______________
b. How much should you expect to win if you play the game once?
______________
c. After breaking the bank at the casino playing this card game, you decide to open your own casino where the customers can play your favorite card game. How much should you charge the players if you want to have an average profit of $1 per play?
______________

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
39
Let x denote the weight gain in pounds per month for a calf. The probability distribution of x is shown below.
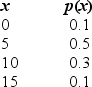
a. Find the average weight gain in pounds per month for a calf.
______________
b. Find the variance of the weight gain.
______________
c. What is
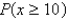 ?
?
______________
d. What is
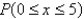 ?
?
______________
e. What is
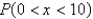 ?
?
______________
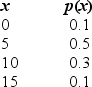
a. Find the average weight gain in pounds per month for a calf.
______________
b. Find the variance of the weight gain.
______________
c. What is
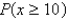 ?
?______________
d. What is
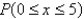 ?
?______________
e. What is
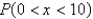 ?
?______________

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
40
Given a set of events 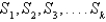 that are mutually exclusive and exhaustive and an event A, the law of total probability states that P(A) can be expressed as
that are mutually exclusive and exhaustive and an event A, the law of total probability states that P(A) can be expressed as 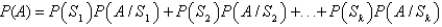 .
.
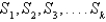 that are mutually exclusive and exhaustive and an event A, the law of total probability states that P(A) can be expressed as
that are mutually exclusive and exhaustive and an event A, the law of total probability states that P(A) can be expressed as 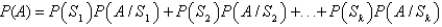 .
.
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
41
If P(A) = 0, P(B) = 0.4, and P(A  B) = 0, then events A and B are independent.
B) = 0, then events A and B are independent.
 B) = 0, then events A and B are independent.
B) = 0, then events A and B are independent.
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
42
If P(A) = 0.4, P(B) = 0.5, and P(A 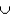 B) = 0.7, then P(A
B) = 0.7, then P(A  B) = 0.2.
B) = 0.2.
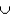 B) = 0.7, then P(A
B) = 0.7, then P(A  B) = 0.2.
B) = 0.2.
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
43
The complement of an event A, denoted by 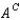 , consists of all the simple events in the sample space S that are not in A.
, consists of all the simple events in the sample space S that are not in A.
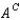 , consists of all the simple events in the sample space S that are not in A.
, consists of all the simple events in the sample space S that are not in A.
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
44
If P(A) = 0.60, P(B) = 0.40, and P(B / A) = 0.60, then P(A / B) = 0.24.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
45
Suppose A and B are mutually exclusive events where P(A) = 0.2 and P(B) = 0.3. Then P(A 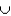 B) = 0.5.
B) = 0.5.
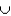 B) = 0.5.
B) = 0.5.
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
46
The intersection of events A and B is the event that A or B or both occur.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
47
Two events A and B are said to be independent if and only if P(A / B) = P(B) or P(B / A) = P(A).

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
48
If P(A) > 0, P(B) > 0, and P(A  B) = 0, then the events A and B are independent.
B) = 0, then the events A and B are independent.
 B) = 0, then the events A and B are independent.
B) = 0, then the events A and B are independent.
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
49
If P(A) = 0.4, P(B) = 0.5, and P(A  B) = 0.20, then the events A and B are mutually exclusive.
B) = 0.20, then the events A and B are mutually exclusive.
 B) = 0.20, then the events A and B are mutually exclusive.
B) = 0.20, then the events A and B are mutually exclusive.
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
50
If P(A) = 0.3, P(A 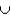 B) = 0.7, and P(A
B) = 0.7, and P(A  B) = 0.2, then P(B) = 0.2.
B) = 0.2, then P(B) = 0.2.
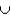 B) = 0.7, and P(A
B) = 0.7, and P(A  B) = 0.2, then P(B) = 0.2.
B) = 0.2, then P(B) = 0.2.
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
51
If A and B are independent events with P(A) = 0.30 and P(B) = 0.50, then P(A/B) is 0.15.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
52
The conditional probability of event B, given that event A has occurred is defined by: 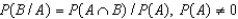 .
.
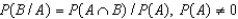 .
.
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
53
If A and B are two independent events with P(A) = 0.25 and P(B) = 0.45, then P(A  B) = 0.70.
B) = 0.70.
 B) = 0.70.
B) = 0.70.
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
54
The probability that event A will not occur is 1- 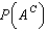 .
.
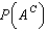 .
.
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
55
Conditional probability is the probability that an event will occur, with no other events taken into consideration.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
56
Two events A and B are said to be independent if P(A  B) = P(A) + P(B).
B) = P(A) + P(B).
 B) = P(A) + P(B).
B) = P(A) + P(B).
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
57
Suppose A and B are mutually exclusive events where P(A) = 0.1 and P(B) = 0.7, then P(A  B) = 0.8.
B) = 0.8.
 B) = 0.8.
B) = 0.8.
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
58
If P(A) > 0 and P(B) > 0, then when A and B are mutually exclusive events, they are also dependent events.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
59
Two events A and B are said to mutually exclusive if P(A  B) = 0.
B) = 0.
 B) = 0.
B) = 0.
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
60
If P(A / B) = P(A), then events A and B are said to be independent.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
61
The additive rule of probability is used to compute the probability for an intersection of two or more events: namely, given two events A and B, 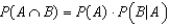 and also
and also 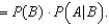
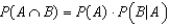 and also
and also 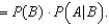

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
62
Which of the following best describes the concept of marginal probability?
A) It is a measure of the likelihood that a particular event will occur, regardless of whether another event occurs.
B) It is a measure of the likelihood that a particular event will occur, given the fact that another event has already occurred or is certain to occur.
C) It is a measure of the likelihood of the simultaneous occurrence of two or more events.
D) It is a direct way for defining the sample space of an experiment.
E) It is a measure of the likelihood that a particular event will not occur.
A) It is a measure of the likelihood that a particular event will occur, regardless of whether another event occurs.
B) It is a measure of the likelihood that a particular event will occur, given the fact that another event has already occurred or is certain to occur.
C) It is a measure of the likelihood of the simultaneous occurrence of two or more events.
D) It is a direct way for defining the sample space of an experiment.
E) It is a measure of the likelihood that a particular event will not occur.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
63
Which one of the following is always true for two events, A and B?
A) If A and B are independent, they are also mutually exclusive.
B) If A and B are dependent, they are also mutually exclusive.
C) If P(A / B) = P(AB), A and B are independent.
D) If A and B are mutually exclusive, then AB can never occur on the same trial of an experiment.
E) All of these.
A) If A and B are independent, they are also mutually exclusive.
B) If A and B are dependent, they are also mutually exclusive.
C) If P(A / B) = P(AB), A and B are independent.
D) If A and B are mutually exclusive, then AB can never occur on the same trial of an experiment.
E) All of these.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
64
A missile designed to destroy enemy satellites has a 0.80 chance of destroying its target. If the government tests three missiles by firing them at a target, what is the probability all three fail to destroy the target? (Assume the missiles perform independently.)
______________
______________

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
65
All the outcomes contained in one or the other of two events (or possibly in both) constitute the union of two events.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
66
If P(A) = 0.40, P(B) = 0.30 and P(A  B) = 0.12, then A and B are:
B) = 0.12, then A and B are:
A) dependent events
B) independent events
C) mutually exclusive events
D) disjoint events
E) none of these
 B) = 0.12, then A and B are:
B) = 0.12, then A and B are:A) dependent events
B) independent events
C) mutually exclusive events
D) disjoint events
E) none of these

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
67
Suppose A and B are events where P(A) = 0.4, P(B) = 0.5, and P(A  B) = 0.2. Then P(B / A) = 0.4.
B) = 0.2. Then P(B / A) = 0.4.
 B) = 0.2. Then P(B / A) = 0.4.
B) = 0.2. Then P(B / A) = 0.4.
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
68
All the outcomes (simple events) contained in one or the other of two random events, or possibly in both, make up:
A) the events of an experiment
B) the intersection of two events
C) the probability space of an experiment
D) the union of two events
E) the complement of the other event
A) the events of an experiment
B) the intersection of two events
C) the probability space of an experiment
D) the union of two events
E) the complement of the other event

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
69
Studies have shown a particular television commercial is understood by 25% of first grade students and 80% of fourth grade students. If a television advertising agency randomly selects one first grader and one fourth grader, what is the probability neither child would understand the commercial, assuming the children's reactions are independent?
______________
______________

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
70
If P(A) = 0.42 and P(B) = 0.38, then P(A  B) is:
B) is:
A) 0.80
B) 0.58
C) 0.04
D) 0.42
E) Cannot be determined from the given information.
 B) is:
B) is:A) 0.80
B) 0.58
C) 0.04
D) 0.42
E) Cannot be determined from the given information.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
71
If P(A) = 0.30, P(B) = 0.40 and P(A  B) = 0.20, then P(A / B) is:
B) = 0.20, then P(A / B) is:
A) 0.12
B) 0.08
C) 0.67
D) 0.50
E) 0.3
 B) = 0.20, then P(A / B) is:
B) = 0.20, then P(A / B) is:A) 0.12
B) 0.08
C) 0.67
D) 0.50
E) 0.3

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
72
The probability of an event and the probability of its complement always sum to:
A) -1
B) 0
C) 1
D) any value between 0 and 1
E) 0.5
A) -1
B) 0
C) 1
D) any value between 0 and 1
E) 0.5

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
73
If events A and B are mutually exclusive, then the probability of both events occurring simultaneously is equal to:
A) -1
B) 0
C) 1
D) any value between 0 and 1
E) 0.5
A) -1
B) 0
C) 1
D) any value between 0 and 1
E) 0.5

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
74
Two events A and B are said to be dependent if and only if:
A) P(A) = P(B)
B) P(A) increases along with P(B)
C) P(A) increases as P(B) decreases
D) event A is affected or changed by the occurrence of event B
E) P(A) < P(B)
A) P(A) = P(B)
B) P(A) increases along with P(B)
C) P(A) increases as P(B) decreases
D) event A is affected or changed by the occurrence of event B
E) P(A) < P(B)

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
75
Suppose P(A) = 0.4, P(B) = 0.3, and P(A  B) = 0. Which one of the following statements correctly defines the relationship between events A and B?
B) = 0. Which one of the following statements correctly defines the relationship between events A and B?
A) Events A and B are independent, but not mutually exclusive.
B) Events A and B are mutually exclusive, but not independent.
C) Events A and B are neither mutually exclusive nor independent.
D) Events A and B are both mutually exclusive and independent.
E) None of these.
 B) = 0. Which one of the following statements correctly defines the relationship between events A and B?
B) = 0. Which one of the following statements correctly defines the relationship between events A and B?A) Events A and B are independent, but not mutually exclusive.
B) Events A and B are mutually exclusive, but not independent.
C) Events A and B are neither mutually exclusive nor independent.
D) Events A and B are both mutually exclusive and independent.
E) None of these.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
76
Which of the following clearly describes the general multiplicative rule of probability?
A) It is a rule of probability theory that is used to compute the probability for the occurrence of a union of two or more events: for any two events, A and B,.
B) It is a rule of probability theory that is used to compute the probability for the occurrence of a union of two or more events: for any two events A and B,.
C) It is a rule of probability theory that is used to compute the probability for an intersection of two or more events: for any two events, A and B,
D) It is a rule of probability theory that is used to compute the probability for an intersection of two or more events: for any two events A and B,
E) All of these.
A) It is a rule of probability theory that is used to compute the probability for the occurrence of a union of two or more events: for any two events, A and B,.
B) It is a rule of probability theory that is used to compute the probability for the occurrence of a union of two or more events: for any two events A and B,.
C) It is a rule of probability theory that is used to compute the probability for an intersection of two or more events: for any two events, A and B,
D) It is a rule of probability theory that is used to compute the probability for an intersection of two or more events: for any two events A and B,
E) All of these.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
77
If P(A) = 0.80, P(B) = 0.70 and P(A 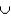 B) = 0.90, then P(A
B) = 0.90, then P(A  B) is:
B) is:
A) 0.60
B) 0.56
C) 0.72
D) 0.63
E) 0.5
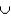 B) = 0.90, then P(A
B) = 0.90, then P(A  B) is:
B) is:A) 0.60
B) 0.56
C) 0.72
D) 0.63
E) 0.5

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
78
An election is being held to fill two "at large" city council seats. Two Republicans and three Democrats are running for office. Assume the candidates are equally likely to be elected, and independent of each other.
a. What are the possible outcomes of the election?
______________
b. What is the probability both seats are filled by Republicans?
______________
c. What is the probability one Republican and one Democrat are elected to the two city council seats?
______________
a. What are the possible outcomes of the election?
______________
b. What is the probability both seats are filled by Republicans?
______________
c. What is the probability one Republican and one Democrat are elected to the two city council seats?
______________

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
79
If P(A/B) = P(A), or P(B/A) = P(B), then events A and B are said to be:
A) mutually exclusive
B) disjoint
C) independent
D) dependent
E) B contains A.
A) mutually exclusive
B) disjoint
C) independent
D) dependent
E) B contains A.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
80
The addition law of probability theory is used to compute the probability for the occurrence of a union of two or more events; namely, given two events A and B, 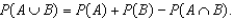
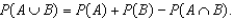

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck


