Exam 4: Probability and Probability Distributions

A false positive in screening (e.g., home pregnancy tests) represents the event that:

All the outcomes (simple events) contained in one or the other of two random events, or possibly in both, make up:

Medical case histories indicate that different illnesses may produce identical symptom. Suppose a particular set of symptoms, which we will denote as event H, occurs only when any one of these illnesses: A, B, or C occurs. (For the sake of simplicity, we will assume that illnesses A, B, and C are mutually exclusive.) Studies show these probabilities of getting the three illnesses: 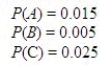The probabilities of developing the symptoms H, given a specific illness, are: 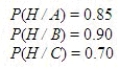Assuming that an ill person shows the symptoms H, what is the probability that the person has illness A? Round your answer to four decimal places. ______________

Probability is the tool that allows the statistician to use sample information to make inferences about or describe the population from which the sample was drawn.

Which one of the following is always true for two events, A and B?

Which of the following statements is false?

An experiment is any activity that results in one and only one of several clearly defined possible outcomes but that does not allow us to tell in advance which of these will prevail in any particular instance.

A university in Alabama has 1000 employees. Four hundred of the employees have at least 20 years of experience (event A), 100 are African American (event B), and 300 with a background in Microsoft Office 2003 (event C). Assume events A, B, and C are independent. a. What is the probability of finding an employee who meets all three of these criteria? ______________ b. What is the probability of finding an employee who meets at least two of the three criteria? ______________

Two events A and B are said to be independent if and only if P(A / B) = P(B) or P(B / A) = P(A).

The probability of an event A is equal to the sum of the probabilities of the simple events contained in A.

A hand soap manufacturer introduced a new liquid, lotion-enriched, antibacterial soap and conducted an extensive consumer survey to help judge the success of the new product. The survey showed 40% of the consumers had seen an advertisement for the new soap, 20% had tried the new soap, and 15% had both seen an advertisement and tried the new soap. Let event A denote that the consumers had seen an ad for the new soap, and event B denote that the consumers had tried the new soap. a. What is the probability a randomly selected consumer had either seen an advertisement or tried the new soap? ______________ b. If a randomly chosen consumer has seen an advertisement for the new soap, what is the probability he or she has tried the product? ______________

If P(A) = 0.40, P(B) = 0.30 and P(A B) = 0.12, then A and B are:

If A and B are independent events with P(A) = 0.30 and P(B) = 0.50, then P(A/B) is 0.15.

How many different combinations of 5 students can be drawn from a class of 25 students? ______________

The expected number of heads in 500 tosses of an unbiased coin is:

Suppose that P(A) = 0.6, P(B) = 0.7, and that events A and B are independent. a. Fi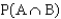nd . ______________ b. Find 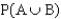. ______________ c. Find P (A / B). ______________ d. Find P (B / A). ______________

Suppose A and B are events where P(A) = 0.4, P(B) = 0.5, and P(A B) = 0.2. Then P(B / A) = 0.4.

If P(A) = 0.80, P(B) = 0.70 and P(A 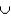B) = 0.90, then P(A B) is:

Three randomly chosen fourteen-year-old junior high students who had not yet taken driver's education classes were given the written part of the Michigan Driver's Exam. Each student was graded as passing (P) or failing (F) the written exam. a.Describe the sample space; that is, list all possible combinations of the three students' grades. __________________________________________ b.Assuming each combination in part (a) is equally likely, what is the probability all three students fail? ______________ c.Assuming each combination in part (a) is equally likely, what is the probability at least one student passes the written test? ______________ d.Assuming each combination in part (a) is equally likely, and if you knew at least one student passed the test, what is the probability all three students passed the test? ______________

Lily frequents one of two fast food restaurants, choosing McDonald 25% of the time and Burger King 75% of the time. Regardless of where she goes, she buys French Fries on 60% of her visits. a. The next time Lily goes into a fast food restaurant, what is the probability that she goes to McDonald and orders a French Fries? ______________ b. Are the two events in the previous question independent? Explain. ______________ c. Explain. ________________________________________________________ d. If Lily goes to a fast food restaurant and orders French Fries, what is the probability that she is at Burger King? ______________ e. What is the probability that Lily goes to McDonald, or orders French Fries, or both? ______________