Deck 5: Several Useful Discrete Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/129
Play
Full screen (f)
Deck 5: Several Useful Discrete Distributions
1
The hypergeometric probability distribution is identical to:
A) the binomial distribution
B) the Poisson distribution
C) any continuous probability distribution
D) none of these
A) the binomial distribution
B) the Poisson distribution
C) any continuous probability distribution
D) none of these
none of these
2
Hypergeometric probability distributions is an example of continuous probability distribution.
False
3
Using the hypergeometric formula, 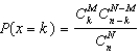 :
:
A) we calculate the probability of k successes when a random sample of size n is drawn without replacement from a population of size N within which M units have the characteristic that denotes success
B) we assume that k = 0, 1, 2, ....n or M (whichever is smaller)
C) we assume that n < N and M < N
D) all of these are true
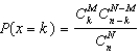 :
:A) we calculate the probability of k successes when a random sample of size n is drawn without replacement from a population of size N within which M units have the characteristic that denotes success
B) we assume that k = 0, 1, 2, ....n or M (whichever is smaller)
C) we assume that n < N and M < N
D) all of these are true
all of these are true
4
A warehouse contains six parts made by company A and ten parts made by company B. If four parts are selected at random from the warehouse, the probability that all four parts are from company B is approximately .008.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
5
A hypergeometric probability distribution shows the probabilities associated with possible values of a discrete random variable when these values are generated by sampling with replacement and the probability of success, therefore, changes from one trial to the next.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
6
When sampling without replacement, the appropriate probability distribution is:
A) a binomial distribution
B) a hypergeometric distribution
C) a Poisson distribution
D) all of these
A) a binomial distribution
B) a hypergeometric distribution
C) a Poisson distribution
D) all of these

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
7
The hypergeometric random variable is the number of successes achieved when a random sample of size n is drawn with replacement from a population of size N within which M units have the characteristic that denotes success.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
8
A random sample of 4 units is taken from a group of 15 items in which 4 units are known to be defective. Assume that sampling occurs without replacement, and the random variable x represents the number of defective units found in the sample.
The mean of the random variable x is:
______________
The variance of the random variable x is:
______________
P(x = 0) = ______________
P(x = 1) = ______________
P(x = 2) = ______________
P(x = 3) = ______________
P(x = 4) = ______________
The mean of the random variable x is:
______________
The variance of the random variable x is:
______________
P(x = 0) = ______________
P(x = 1) = ______________
P(x = 2) = ______________
P(x = 3) = ______________
P(x = 4) = ______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
9
A warehouse contains six parts made by company A and ten parts made by company B. If four parts are selected at random from the warehouse, the probability that none of the four parts is from company A is approximately .1154.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
10
A student has decided to rent three movies for a three-day weekend. If there are 4 action movies and 6 romance movies that are of equal interest to the student, what is the probability that the student will select 1 romance movie and 2 action movies?
______________
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
11
Hypergeometric probability distributions is an example of discrete probability distributions.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
12
Given that n is the number of trials of a random experiment, N is population size, M is the number of population units with the "success" characteristic, and p is the probability of success in the first trial, the mean of the hypergeometric random variable's probability distribution always equals:
A) n
B) np
C) n(N/M)
D) none of these
A) n
B) np
C) n(N/M)
D) none of these

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
13
The hypergeometric probability distribution is used rather than the binomial distribution when the sampling is performed:
A) with replacement from a finite population
B) without replacement from a finite population of size N and that size N is small in relation to the sample size n namely, n / N.05
C) without replacement from an infinite population
D) with replacement from an infinite population
A) with replacement from a finite population
B) without replacement from a finite population of size N and that size N is small in relation to the sample size n namely, n / N.05
C) without replacement from an infinite population
D) with replacement from an infinite population

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
14
A professor has received a grant to travel to an archaeological dig site. The grant includes funding for five graduate students. If there are five male and four female graduate students eligible and equally qualified, what is the probability that the professor will select three male and two female graduate students to accompany her to the dig site?
______________
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
15
A small community college in Ohio has four student organizations (A, B, C, and D). Organization A has 5 students, B has 8, C has 10, and D has 12. It is thought that new students have no preference for one of these organizations over the other. If seven new students are admitted to the college, what is the probability that one student will choose organization A, one will choose B, two will choose C, and three will choose D?
A) approximately .059
B) .200
C) approximately .243
D) Cannot be determined without additional information.
A) approximately .059
B) .200
C) approximately .243
D) Cannot be determined without additional information.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
16
Let x be a hypergeometric random variable with N = 12, n = 4, and M = 3.
Calculate p(0).
______________
Calculate p(1).
______________
Calculate p(2).
______________
Calculate p(3).
______________
Calculate the mean.
______________
Calculate the variance.
______________
What proportion of the population of measurements fall into the interval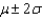 ?
?
______________
Into the interval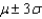 ?
?
______________
Do these results agree with those given by Tchebysheff's Theorem?
______________
Calculate p(0).
______________
Calculate p(1).
______________
Calculate p(2).
______________
Calculate p(3).
______________
Calculate the mean.
______________
Calculate the variance.
______________
What proportion of the population of measurements fall into the interval
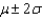 ?
?______________
Into the interval
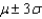 ?
?______________
Do these results agree with those given by Tchebysheff's Theorem?
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
17
A company has five applicants for two positions: three women and two men. Suppose that the five applicants are equally qualified and that no preference is given for choosing either gender. Let x equal the number of men chosen to fill the two positions.
What is the mean of the probability distribution of x?
______________
What is the variance of the probability distribution of x?
______________
What is the standard deviation of the probability distribution of x?
______________
What is the mean of the probability distribution of x?
______________
What is the variance of the probability distribution of x?
______________
What is the standard deviation of the probability distribution of x?
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
18
The hypergeometric probability distribution:
A) provides probabilities associated with possible values of a binomial random variable in situations in which these values are generated by sampling a finite population
B) provides probabilities associated with possible values of a binomial random variable in situations in which sampling is done without replacement
C) provides probabilities associated with possible values of a binomial random variable in situations in which the probability of success changes from one trial to the next
D) is correctly described by all of these
A) provides probabilities associated with possible values of a binomial random variable in situations in which these values are generated by sampling a finite population
B) provides probabilities associated with possible values of a binomial random variable in situations in which sampling is done without replacement
C) provides probabilities associated with possible values of a binomial random variable in situations in which the probability of success changes from one trial to the next
D) is correctly described by all of these

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
19
The hypergeometric probability distribution formula calculates the probability of x successes when a random sample of size n is drawn without replacement from a population of size N within which M units have the characteristic that denotes success, and N - M units have the characteristic that denotes failure.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
20
A warehouse contains six parts made by company A and ten parts made by company B. If four parts are selected at random from the warehouse, the probability that one of the four parts is from company B is approximately .1099.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
21
A college has seven applicants for three scholarships: four females and three males. Suppose that the seven applicants are equally qualified and that no preference is given by the selection committee for choosing either gender. Let x equal the number of female students chosen for the three scholarships.
What is the mean of the distribution of x?
______________
What is the variance of the distribution of x?
______________
What is the probability that only one female will receive a scholarship?
______________
What is the probability that two females will receive a scholarship?
______________
What is the probability that none of the three males will receive a scholarship?
______________
What is the probability that none of the four females will receive a scholarship?
______________
What is the mean of the distribution of x?
______________
What is the variance of the distribution of x?
______________
What is the probability that only one female will receive a scholarship?
______________
What is the probability that two females will receive a scholarship?
______________
What is the probability that none of the three males will receive a scholarship?
______________
What is the probability that none of the four females will receive a scholarship?
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
22
Which of the following cannot generate a Poisson distribution?
A) The number of telephone calls received by a switchboard in a specified time period.
B) The number of customers arriving at a gas station on Christmas day.
C) The number of bacteria found in a cubic yard of soil.
D) The number of children in a family.
E) The number of accidents per day on a certain section of a highway.
A) The number of telephone calls received by a switchboard in a specified time period.
B) The number of customers arriving at a gas station on Christmas day.
C) The number of bacteria found in a cubic yard of soil.
D) The number of children in a family.
E) The number of accidents per day on a certain section of a highway.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
23
Poisson distribution is appropriate to determine the probability of a given number of defective items in a shipment.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
24
The mean and variance of the Poisson distribution are equal.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
25
In a Poisson problem, x represents the number of events occurring in a period of time or space during which an average of 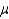 such events can be expected to occur.
such events can be expected to occur.
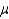 such events can be expected to occur.
such events can be expected to occur.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
26
The Poisson parameter 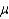 is the mean number of occurrences of an event per unit of time or space during the Poisson process.
is the mean number of occurrences of an event per unit of time or space during the Poisson process.
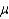 is the mean number of occurrences of an event per unit of time or space during the Poisson process.
is the mean number of occurrences of an event per unit of time or space during the Poisson process.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
27
The Poisson probability distribution provides good approximations to binomial probabilities when n is large and 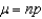 is small, preferably with np < 7.
is small, preferably with np < 7.
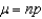 is small, preferably with np < 7.
is small, preferably with np < 7.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
28
The Poisson random variable is:
A) a continuous random variable with infinitely many possible values
B) a discrete random variable with infinitely many possible values
C) a continuous random variable with finite number of possible values
D) a discrete random variable with finite number of possible values
E) all of these
A) a continuous random variable with infinitely many possible values
B) a discrete random variable with infinitely many possible values
C) a continuous random variable with finite number of possible values
D) a discrete random variable with finite number of possible values
E) all of these

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
29
Given a Poisson random variable x, where the average number of times an event occurs in a certain period of time is 2.5, then P(x = 0) is:
A) 2.5
B) 0.0821
C) 1.5811
D) 0.40
E) 1
A) 2.5
B) 0.0821
C) 1.5811
D) 0.40
E) 1

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
30
A Poisson process is the occurrence of a series of events of a given type in a random pattern over time or space such that (1) the number of occurrences within a specified time or space can equal any integer between zero and infinity, (2) the number of occurrences within one unit of time or space is independent of that in any other such (non-overlapping) unit, and (3) the probability of occurrences is the same in all such units.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
31
The Poisson probability distribution is an example of continuous probability distribution.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
32
Which probability distribution is appropriate when the events of interest occur randomly, independently of one another, and rarely?
A) Binomial distribution
B) Poisson distribution
C) Hypergeometric distribution
D) any discrete probability distribution
E) all of these
A) Binomial distribution
B) Poisson distribution
C) Hypergeometric distribution
D) any discrete probability distribution
E) all of these

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
33
The Poisson probability distribution is an example of a continuous probability distribution.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
34
The mean of a Poisson distribution, where 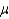 is the average number of successes occurring in a specified interval, is
is the average number of successes occurring in a specified interval, is 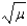 .
.
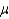 is the average number of successes occurring in a specified interval, is
is the average number of successes occurring in a specified interval, is 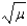 .
.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
35
The Poisson probability tables list the probabilities of x occurrences in a Poisson process for various values of 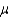 , the mean number of occurrences.
, the mean number of occurrences.
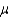 , the mean number of occurrences.
, the mean number of occurrences.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
36
The Poisson random variable is the number of successes achieved when a random sample of size n is drawn without replacement from a population of size N within which M units have the characteristic that denotes success.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
37
The Poisson distribution is applied to events for which the probability of occurrence over a given span of time, space, or distance is very small.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
38
The Poisson distribution is applied to events for which the probability of occurrence over a given span of time, space, or distance is large.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
39
The probability distribution of a Poisson random variable provides a good model for data that represent the number of occurrences of a specified event in a given unit of time or space.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
40
Which of the following experiments can be modeled by the Poisson distribution?
A) The number of calls received by a switchboard during a given period of time.
B) The number of bacteria per small volume of fluid.
C) The number of customer arrivals at a checkout counter during a given minute.
D) The number of customer arrivals at a checkout counter during a given hour.
E) All of these.
A) The number of calls received by a switchboard during a given period of time.
B) The number of bacteria per small volume of fluid.
C) The number of customer arrivals at a checkout counter during a given minute.
D) The number of customer arrivals at a checkout counter during a given hour.
E) All of these.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
41
The number of traffic accidents per day on a certain section of highway is thought to be Poisson distributed with a mean equal 2.19. Then the standard deviation of number of accidents is:
A) 2.19
B) approximately 4.80
C) approximately 1.48
D) 3.14
E) (2.19) 2
A) 2.19
B) approximately 4.80
C) approximately 1.48
D) 3.14
E) (2.19) 2

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
42
The number of teleport inquiries x in a timesharing computer system averages 0.2 per millisecond and follows a Poisson distribution.
Find the probability no inquiries are made during the next millisecond.
______________
Find the probability no inquiries are made during the next 3 milliseconds.
______________
Find the probability no inquiries are made during the next millisecond.
______________
Find the probability no inquiries are made during the next 3 milliseconds.
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
43
In a book, 2 misprints occur per 100 pages. Using the cumulative Poisson probability table available in your text, we can determine which of the following probabilities in a book of 500 pages?
A) The probability of finding between 5 and 6 misprints equals .099.
B) The probability of finding at least 20 misprints equals .003.
C) The probability of finding at least 24 misprints equals .1234.
D) The probability of finding at least 20 misprints equals 1.
E) The probability of finding at least 24misprints equals 1.
A) The probability of finding between 5 and 6 misprints equals .099.
B) The probability of finding at least 20 misprints equals .003.
C) The probability of finding at least 24 misprints equals .1234.
D) The probability of finding at least 20 misprints equals 1.
E) The probability of finding at least 24misprints equals 1.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
44
The probability the 1993-94 flu vaccine immunizes those receiving it is 0.97. If a random sample of 200 people receive the vaccine, what is the probability the vaccine will be ineffective on at most 5 people?
______________
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
45
A salesperson has found the probability of making a sale on a particular product manufactured by his or her company is 0.05. If the salesperson contacts 140 potential customers, what is the probability he or she will sell at least 2 of these products?
______________
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
46
Which of the following correctly describes a Poisson random variable?
A) It does not generate a binomial either/or outcome because only a single type of outcome or "event" is occurring during the Poisson process.
B) It is not confined to a fixed number of trials, because its value can equal any discrete integer between zero and infinity, along a continuum of time or space.
C) It equals the number of occurrences of a specified event within a specified time or space.
D) All of these.
E) None of these.
A) It does not generate a binomial either/or outcome because only a single type of outcome or "event" is occurring during the Poisson process.
B) It is not confined to a fixed number of trials, because its value can equal any discrete integer between zero and infinity, along a continuum of time or space.
C) It equals the number of occurrences of a specified event within a specified time or space.
D) All of these.
E) None of these.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
47
Which of the following distributions could not be used to describe the exact distribution for a continuous random variable?
A) Binomial distribution
B) Poisson distribution
C) Hypergeometric distribution
D) all of these
E) none of these
A) Binomial distribution
B) Poisson distribution
C) Hypergeometric distribution
D) all of these
E) none of these

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
48
The quality of computer disks is measured by sending the disks through a certifier which counts the number of missing pulses. A certain brand of computer disks averages 0.1 missing pulse per disk. Let the random variable x denote the number of missing pulses.
What is the distribution of x?
Type of distribution:
______________
Mean of distribution:
______________
Find the probability the next inspected disk will have no missing pulse.
______________
Find the probability the next disk inspected will have more than one missing pulse.
______________
Find the probability neither of the next two disks inspected will contain any missing pulse.
______________
What is the distribution of x?
Type of distribution:
______________
Mean of distribution:
______________
Find the probability the next inspected disk will have no missing pulse.
______________
Find the probability the next disk inspected will have more than one missing pulse.
______________
Find the probability neither of the next two disks inspected will contain any missing pulse.
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
49
Consider an experiment with 25 trials where the probability of success on any trial is 0.01, and let the random variable x be the number of successes among the 25 trials.
Using the Poisson approximation to the binomial, what are:
p(0) = ______________
p(1) = ______________
p(2) = ______________
p(3) = ______________
Using the Poisson approximation to the binomial, what are:
p(0) = ______________
p(1) = ______________
p(2) = ______________
p(3) = ______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
50
Which of the following statements is false with respect to a Poisson distribution?
A) The Poisson distribution is an example of a discrete probability distribution.
B) The Poisson distribution is more skewed to the right for smaller values of the parameter.
C) The Poisson distribution is symmetrical when the value of the parameteris close to 5.
D) The mean of the Poisson distribution is equal to the variance.
E) All of these.
A) The Poisson distribution is an example of a discrete probability distribution.
B) The Poisson distribution is more skewed to the right for smaller values of the parameter.
C) The Poisson distribution is symmetrical when the value of the parameteris close to 5.
D) The mean of the Poisson distribution is equal to the variance.
E) All of these.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
51
An eight-cylinder automobile engine has two misfiring spark plugs. The mechanic removes all four plugs from one side of the engine.
What is the probability the two misfiring spark plugs are among those removed?
______________
What is the mean number of misfiring spark plugs?
______________
What is the variance of the number of misfiring spark plugs?
______________
What is the probability the two misfiring spark plugs are among those removed?
______________
What is the mean number of misfiring spark plugs?
______________
What is the variance of the number of misfiring spark plugs?
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
52
Let the random variable x have the Poisson distribution with mean 3.
What is the probability x will fall in the interval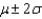 ?
?
______________
What is the probability x will fall in the interval
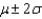 ?
?______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
53
Rebuilt ignition systems leave an aircraft repair shop at an average rate of 3 per hour. The assembly line needs four ignition systems in the next hour.
What is the probability they will be available?
______________
What is the probability they will be available?
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
54
The number of telephone calls coming into a business' switchboard averages 4 calls per minute. Let x be the number of calls received.
Find P(x = 0).
______________
What is the probability there will be at least one call in a given one-minute period?
______________
What is the probability at least one call will be received in a given two-minute period?
______________
Find P(x = 0).
______________
What is the probability there will be at least one call in a given one-minute period?
______________
What is the probability at least one call will be received in a given two-minute period?
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
55
A warehouse contains 10 computer printers, 4 of which are defective. A company randomly selects five of the 10 printers to purchase.
What is the probability all 5 are nondefective?
______________
What is the mean of x?
______________
What is the variance of x?
______________
What is the probability all 5 are nondefective?
______________
What is the mean of x?
______________
What is the variance of x?
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
56
The number of traffic accidents per day on a certain section of highway is thought to be Poisson distributed with a mean equal 2.19. Then the probability of no accidents on this section of highway during one day period is approximately:
A) 0.457
B) 0.112
C) 0.318
D) 0.296
E) 0.211
A) 0.457
B) 0.112
C) 0.318
D) 0.296
E) 0.211

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
57
Given a Poisson random variable x, where the average number of times an event occurs in a certain period of time or space is 1.5, then P(x = 2) is:
A) 0.2231
B) 0.5020
C) 0.2510
D) 0.1116
E) 0.5
A) 0.2231
B) 0.5020
C) 0.2510
D) 0.1116
E) 0.5

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
58
If the standard deviation for a Poisson distribution is known to be 3.60, the expected value of that Poisson distribution is:
A) 3.60
B) approximately 1.90
C) 8.28
D) 12.96
E) 7.2
A) 3.60
B) approximately 1.90
C) 8.28
D) 12.96
E) 7.2

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
59
From a group of 10 bank officers, 3 are selected at random to be relocated and supervise new branch offices. If two of the 10 officers are women and 8 are men, what is the probability exactly one of the officers to be relocated will be a woman?
______________
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
60
The number of traffic accidents per day on a certain section of highway is thought to be Poisson distributed with a mean equal 2.19. Based on this, how many traffic accidents should be expected during a week long period?
A) 15.33
B) 10.95
C) approximately 10.36
D) approximately 12.21
E) none of these
A) 15.33
B) 10.95
C) approximately 10.36
D) approximately 12.21
E) none of these

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
61
The number of successes observed during the n trials of a binomial experiment is called the binomial random variable.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
62
Students arrive at a health center, according to a Poisson distribution, at a rate of 4 every 15 minutes. Let x represent number of students arriving in a 15 minute time period.
What is the probability that no more than 3 students arrive in a 15 minute time period?
______________
What is the probability that exactly 5 students arrive in a 15 minute time period?
______________
What is the probability that more than 5 students arrive in a 15-minute time period?
______________
What is the probability that between 4 and 8 students, inclusively, arrive in a 15-minute time period?
______________
What is the probability that no more than 3 students arrive in a 15 minute time period?
______________
What is the probability that exactly 5 students arrive in a 15 minute time period?
______________
What is the probability that more than 5 students arrive in a 15-minute time period?
______________
What is the probability that between 4 and 8 students, inclusively, arrive in a 15-minute time period?
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
63
Insulin-dependent diabetes (IDD) is a common chronic disorder of children. This disease occurs most frequently in persons of northern European descent. Let us assume that an area in Europe has an incidence of 6 cases per 100,000 per year.
Can the distribution of the number of cases of IDD in this area be approximated by a Poisson distribution?
______________
What is the mean?
______________
What is the probability that the number of cases of IDD in this area is less than or equal to 3 per 100,000?
______________
What is the probability that the number of cases is greater than or equal to 3 but less than or equal to 7 per 100,000?
______________
Would you expect to observe 10 or more cases of IDD per 100,000 in this area in a given year?
______________
Why or why not?
________________________________________________________
Can the distribution of the number of cases of IDD in this area be approximated by a Poisson distribution?
______________
What is the mean?
______________
What is the probability that the number of cases of IDD in this area is less than or equal to 3 per 100,000?
______________
What is the probability that the number of cases is greater than or equal to 3 but less than or equal to 7 per 100,000?
______________
Would you expect to observe 10 or more cases of IDD per 100,000 in this area in a given year?
______________
Why or why not?
________________________________________________________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
64
The number x of people entering the intensive care unit at a particular hospital on any one day has a Poisson probability distribution with mean equal to four persons per day.
What is the probability that the number of people entering the intensive care unit on a particular day is two?
______________
What is the probability that the number of people entering the intensive care unit on a particular day is Less than or equal to two?
______________
Is it likely that x will exceed ten?
______________
Explain.
________________________________________________________
What is the probability that the number of people entering the intensive care unit on a particular day is two?
______________
What is the probability that the number of people entering the intensive care unit on a particular day is Less than or equal to two?
______________
Is it likely that x will exceed ten?
______________
Explain.
________________________________________________________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
65
The binomial probability distribution is an example of discrete probability distributions.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
66
It is known that between 8 and 10 a.m. on Saturdays, cars arrive at a toll station in Indiana at a rate of 60 per hour. Assume that a Poisson process is occurring, and that the random variable x represents the number of cars arriving at the station between 9:00 and 9:05 a.m.
What is the expected number of cars arriving at the toll station between 9:00 and 9:05 a.m.?
______________
What is the standard deviation of the number of cars arriving at the toll station between 9:00 and 9:05 a.m.?
______________
Find P(x = 0).
______________
Find P(x = 2).
______________
Find P(x = 5).
______________
Find P(x = 10).
______________
What is the expected number of cars arriving at the toll station between 9:00 and 9:05 a.m.?
______________
What is the standard deviation of the number of cars arriving at the toll station between 9:00 and 9:05 a.m.?
______________
Find P(x = 0).
______________
Find P(x = 2).
______________
Find P(x = 5).
______________
Find P(x = 10).
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
67
An automobile service center can take care of 8 cars per day. Assume that the cars arrive at the service center randomly and independently of each other at a rate of 6 per hour, on average.
What is the standard deviation of the number of cars that arrive at the center?
______________
What is the probability of the service center being empty in any given hour?
______________
What is the probability that exactly 6 cars will be in the service center at any point during a given hour?
______________
What is the probability that less than 2 cars will be in the service center at any point during a given hour?
______________
What is the standard deviation of the number of cars that arrive at the center?
______________
What is the probability of the service center being empty in any given hour?
______________
What is the probability that exactly 6 cars will be in the service center at any point during a given hour?
______________
What is the probability that less than 2 cars will be in the service center at any point during a given hour?
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
68
As a rule of thumb, if the sample size n is large relative to the population size N in particular, if n / N  0.05 then the resulting experiment will not be binomial.
0.05 then the resulting experiment will not be binomial.
 0.05 then the resulting experiment will not be binomial.
0.05 then the resulting experiment will not be binomial.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
69
It was estimated that 2% of a particular 1997 model minivan had incorrectly installed brake lines. Suppose 300 minivans of this model are selected at random. Let x represent number of minivans with incorrectly installed brake lines.
What is the probability that 9 have incorrectly installed brake lines?
______________
What is the probability that 9 have incorrectly installed brake lines?
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
70
In a binomial experiment, the probability of success is the same on every trial.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
71
A coin toss experiment represents a binomial experiment only if the coin is balanced, i.e., p = 0.5.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
72
The number of people arriving at a bicycle repair shop follows a Poisson distribution with an average of 5 arrivals per hour. Let x represent number of people arriving per hour.
What is the probability that seven people arrive at the bike repair shop in a one hour period of time?
______________
What is the probability that at most seven people arrive at the bike repair shop in a one hour period of time?
______________
What is the probability that more than seven people arrive at the bike repair shop in a one hour period of time?
______________
What is the probability that between 4 and 9 people, inclusively, arrive at the bike repair shop in a one hour period of time?
______________
What is the probability that seven people arrive at the bike repair shop in a one hour period of time?
______________
What is the probability that at most seven people arrive at the bike repair shop in a one hour period of time?
______________
What is the probability that more than seven people arrive at the bike repair shop in a one hour period of time?
______________
What is the probability that between 4 and 9 people, inclusively, arrive at the bike repair shop in a one hour period of time?
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
73
Three yellow and two blue pencils are in a drawer. If we randomly select two pencils from the drawer, find the probability distribution of x, the number of yellow pencils selected.



Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
74
A jug contains 5 black marbles and 5 white marbles well mixed. A marble is removed and its color noted. A second marble is removed, without replacing the first marble, and its color is also noted. If x is the total number of black marbles in the two draws, then x has a binomial distribution.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
75
If x is a binomial random variable with n = 20, and p = 0.5, then P(x = 20) = 1.0.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
76
A binomial experiment is a sequence of n identical trials such that each trial (1) produces one of two outcomes that are conventionally called success and failure and (2) is independent of any other trial so that the probability of success or failure is constant from trial to trial.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
77
A binomial probability distribution shows the probabilities associated with possible values of a discrete random variable that are generated by a binomial experiment.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
78
A package of six light bulbs contains 2 defective bulbs. If three bulbs are selected for use, find the probability none are defective.
______________
______________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
79
The binomial random variable is the number of successes that occur in a certain period of time or space.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
80
A binomial random variable is an example of a discrete random variable.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck


