Exam 5: Several Useful Discrete Distributions
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
A binomial probability distribution shows the probabilities associated with possible values of a discrete random variable that are generated by a binomial experiment.
Free
(True/False)
4.8/5  (25)
(25)
Correct Answer:
True
The mean of a Poisson distribution, where 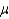 is the average number of successes occurring in a specified interval, is
is the average number of successes occurring in a specified interval, is 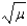 .
.
Free
(True/False)
4.9/5  (36)
(36)
Correct Answer:
False
In a book, 2 misprints occur per 100 pages. Using the cumulative Poisson probability table available in your text, we can determine which of the following probabilities in a book of 500 pages?
Free
(Multiple Choice)
4.8/5  (33)
(33)
Correct Answer:
B
A life insurance salesperson makes 15 sales calls daily. The chance of making a sale on each call is 0.40. The probability that he will make at most 2 sales is less than 0.10.
(True/False)
4.8/5  (34)
(34)
A binomial random variable is an example of a discrete random variable.
(True/False)
4.9/5  (31)
(31)
A company has five applicants for two positions: three women and two men. Suppose that the five applicants are equally qualified and that no preference is given for choosing either gender. Let x equal the number of men chosen to fill the two positions.
What is the mean of the probability distribution of x?
______________
What is the variance of the probability distribution of x?
______________
What is the standard deviation of the probability distribution of x?
______________
(Short Answer)
4.8/5  (37)
(37)
Four in ten Americans who travel by car look for gas and food outlets that are close to or visible from the highway. Suppose a random sample of n = 20 Americans who travel by car are asked how they determine where to stop for food and gas. Let x be the number in the sample who respond that they look for gas and food outlets that are close to or visible from the highway.
Calculate the mean of x.
______________
Calculate the variance of x.
______________
Calculate the interval 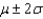 .
______________
What values of the binomial random variable x fall into this interval?
______________
Find
.
______________
What values of the binomial random variable x fall into this interval?
______________
Find 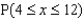 .
______________
How does this compare with the fraction in the interval
.
______________
How does this compare with the fraction in the interval 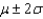 for any distribution? For mound-shaped distributions?
________________________________________________________
for any distribution? For mound-shaped distributions?
________________________________________________________
(Essay)
4.8/5  (24)
(24)
The number of traffic accidents per day on a certain section of highway is thought to be Poisson distributed with a mean equal 2.19. Then the standard deviation of number of accidents is:
(Multiple Choice)
4.8/5  (32)
(32)
The Poisson random variable is the number of successes achieved when a random sample of size n is drawn without replacement from a population of size N within which M units have the characteristic that denotes success.
(True/False)
4.8/5  (36)
(36)
Given a Poisson random variable x, where the average number of times an event occurs in a certain period of time is 2.5, then P(x = 0) is:
(Multiple Choice)
4.8/5  (34)
(34)
From past experience, it is known 90% of one-year-old children can distinguish their mother's voice from the voice of a similar sounding female. A random sample of 20 one-year-olds are given this voice recognition test.
Find the probability at least 3 children do not recognize their mother's voice.
______________
Find the probability all 20 children recognize their mother's voice.
______________
Let the random variable x denote the number of children who do not recognize their mother's voice. Find the mean of x.
______________
Let the random variable x denote the number of children who do not recognize their mother's voice. Find the variance of x.
______________
Find the probability that at most 4 children do not recognize their mother's voice.
______________
(Short Answer)
4.8/5  (46)
(46)
Hotels, like airlines, often overbook, counting on the fact that some people with reservations will cancel at the last minute. A certain hotel chain finds 20% of the reservations will not be used.
If we randomly selected 15 reservations, what is the probability more than 8 but less than 12 reservations will be used?
______________
If four reservations are made, what is the chance fewer than two will cancel?
______________
(Short Answer)
4.8/5  (34)
(34)
A manufacturer of golf balls uses a production process that produces 10 percent defective balls. A quality inspector takes samples of a week's output with replacement. Using the cumulative binomial probability table available in your text, the inspector can determine which of the following probabilities?
(Multiple Choice)
4.7/5  (32)
(32)
It has been alleged that 40 percent of all college students favor Dell computers. If this were true, and we took a random sample of 50 students, the binomial probability table for cumulative values of x available in your text, would reveal which of the following probabilities?
(Multiple Choice)
4.9/5  (36)
(36)
In 1996, the average combined SAT score (math + verbal) for students in the United States was 1013, and 41% of all high school graduates took this test. Suppose that 500 students are randomly selected throughout the United States.
Which of the following random variables has an approximate binomial distribution? The number of students who took the SAT.
____________________________
The scores of the 500 students on the SAT.
____________________________
The number of students who scored above average on the SAT.
____________________________
The amount of time it took each student to complete the SAT.
____________________________
(Essay)
4.9/5  (28)
(28)
Hypergeometric probability distributions is an example of discrete probability distributions.
(True/False)
4.8/5  (33)
(33)
As a rule of thumb, if the sample size n is large relative to the population size N in particular, if n / N  0.05 then the resulting experiment will not be binomial.
0.05 then the resulting experiment will not be binomial.
(True/False)
4.8/5  (41)
(41)
A small community college in Ohio has four student organizations (A, B, C, and D). Organization A has 5 students, B has 8, C has 10, and D has 12. It is thought that new students have no preference for one of these organizations over the other. If seven new students are admitted to the college, what is the probability that one student will choose organization A, one will choose B, two will choose C, and three will choose D?
(Multiple Choice)
4.7/5  (30)
(30)
An oil firm plans to drill 20 wells, each having probability 0.2 of striking oil. Each well costs $20,000 to drill; a well which strikes oil will bring in $750,000 in revenue. Find the expected gain from the 20 wells.
______________
(Short Answer)
4.9/5  (40)
(40)
Showing 1 - 20 of 129
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)