Deck 6: Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/93
Play
Full screen (f)
Deck 6: Differential Equations
1
At time 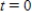 minutes, the temperature of an object is
minutes, the temperature of an object is 
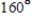 F. The temperature of the object is changing at the rate given by the differential equation
F. The temperature of the object is changing at the rate given by the differential equation 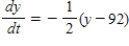 . Use Euler's Method to approximate the particular solutions of this differential equation at
. Use Euler's Method to approximate the particular solutions of this differential equation at 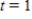 . Use a step size of
. Use a step size of 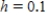 . Round your answer to one decimal place.
. Round your answer to one decimal place.
A) 137.1
B) 139.5
C) 147.4
D) 144.6
E) 132.7
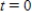 minutes, the temperature of an object is
minutes, the temperature of an object is 
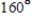 F. The temperature of the object is changing at the rate given by the differential equation
F. The temperature of the object is changing at the rate given by the differential equation 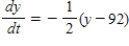 . Use Euler's Method to approximate the particular solutions of this differential equation at
. Use Euler's Method to approximate the particular solutions of this differential equation at 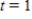 . Use a step size of
. Use a step size of 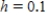 . Round your answer to one decimal place.
. Round your answer to one decimal place. A) 137.1
B) 139.5
C) 147.4
D) 144.6
E) 132.7
E
2
Use integration to find a general solution of the differential equation 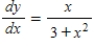 .
.
A)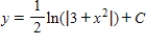
B)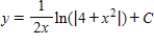
C)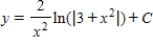
D)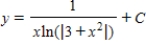
E)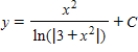
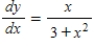 .
. A)
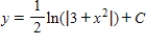
B)
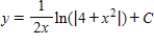
C)
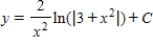
D)
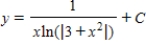
E)
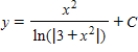
A
3
Determine whether the function 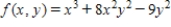 is homogeneous and determine its degree if it is.
is homogeneous and determine its degree if it is.
A) homogeneous, the degree is 3
B) homogeneous, the degree is 4
C) not homogeneous
D) homogeneous, the degree is 2
E) homogeneous, the degree is 1
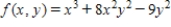 is homogeneous and determine its degree if it is.
is homogeneous and determine its degree if it is. A) homogeneous, the degree is 3
B) homogeneous, the degree is 4
C) not homogeneous
D) homogeneous, the degree is 2
E) homogeneous, the degree is 1
C
4
The half-life of the carbon isotope C-14 is approximately 5,715 years. If the initial quantity of the isotope is 34 g, what is the amount left after 10,000 years? Round your answer to two decimal places.
A) 10.11 g
B) 18.54 g
C) 10.61 g
D) 29.75 g
E) 5.06 g
A) 10.11 g
B) 18.54 g
C) 10.61 g
D) 29.75 g
E) 5.06 g

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
5
The isotope 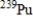 has a half-life of
has a half-life of 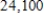 years. Given an initial amount of 16 grams of the isotope, how many grams will remain after 1,000 years? After 10,000 years? Round your answers to four decimal places.
years. Given an initial amount of 16 grams of the isotope, how many grams will remain after 1,000 years? After 10,000 years? Round your answers to four decimal places.
A) 10.8825 g, 8.4006 g
B) 9.3278 g, 7.2005 g
C) 15.5464 g, 12.0008 g
D) 6.2185 g, 4.8003 g
E) 18.6556 g, 14.4010 g
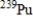 has a half-life of
has a half-life of 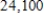 years. Given an initial amount of 16 grams of the isotope, how many grams will remain after 1,000 years? After 10,000 years? Round your answers to four decimal places.
years. Given an initial amount of 16 grams of the isotope, how many grams will remain after 1,000 years? After 10,000 years? Round your answers to four decimal places. A) 10.8825 g, 8.4006 g
B) 9.3278 g, 7.2005 g
C) 15.5464 g, 12.0008 g
D) 6.2185 g, 4.8003 g
E) 18.6556 g, 14.4010 g

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
6
Each of the following graphs is from a logistic function 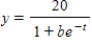 . Which one has the largest value of b?
. Which one has the largest value of b?
A)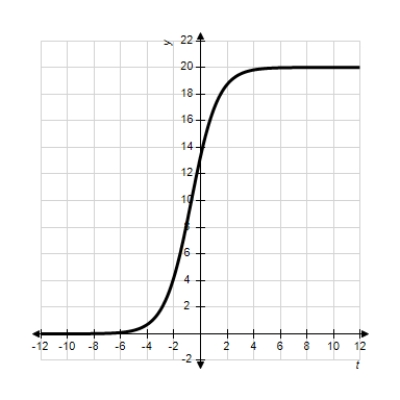
B)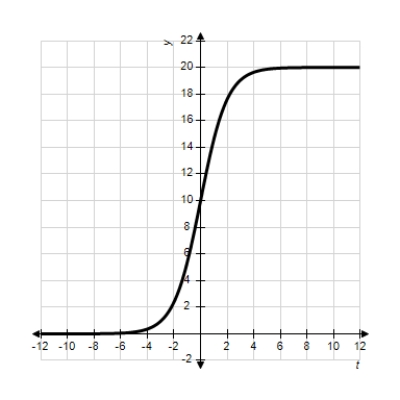
C)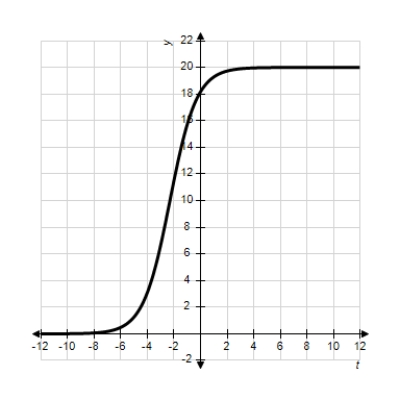
D)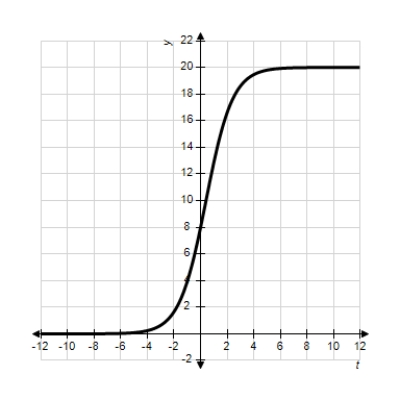
E)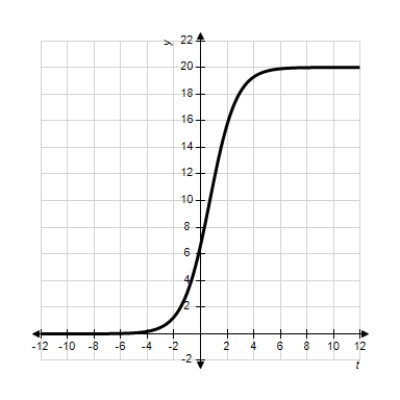
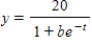 . Which one has the largest value of b?
. Which one has the largest value of b? A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
7
A calf that weighs 50 pounds at birth gains weight at the rate 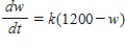 where w is weight in pounds and t is time in years. What is the maximum weight of the animal if one uses the model
where w is weight in pounds and t is time in years. What is the maximum weight of the animal if one uses the model 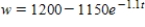 ?
?
A) 1200 lb
B) 750 lb
C) 1150 lb
D) 1250 lb
E) 1900 lb
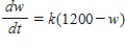 where w is weight in pounds and t is time in years. What is the maximum weight of the animal if one uses the model
where w is weight in pounds and t is time in years. What is the maximum weight of the animal if one uses the model 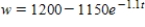 ?
? A) 1200 lb
B) 750 lb
C) 1150 lb
D) 1250 lb
E) 1900 lb

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
8
The rate of change of N is proportional to N. When 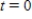 ,
, 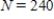 and when
and when 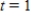 ,
, 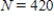 . What is the value of N when
. What is the value of N when 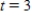 ? Round your answer to three decimal places.
? Round your answer to three decimal places.
A) 1,316.250
B) 1,286.250
C) 1,236.250
D) 140.599
E) 20,580.000
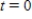 ,
, 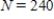 and when
and when 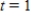 ,
, 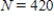 . What is the value of N when
. What is the value of N when 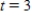 ? Round your answer to three decimal places.
? Round your answer to three decimal places. A) 1,316.250
B) 1,286.250
C) 1,236.250
D) 140.599
E) 20,580.000

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the differential equation. 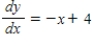
A)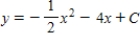
B)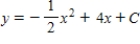
C)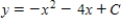
D)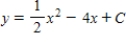
E)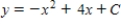
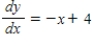
A)
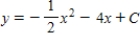
B)
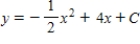
C)
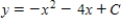
D)
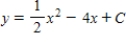
E)
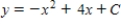

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
10
A 500-gallon tank is half full of distilled water. At time 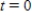 , a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 11 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 9 gallons per minute. At what time will the tank be full?
, a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 11 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 9 gallons per minute. At what time will the tank be full?
A) 250 minutes
B) 126 minutes
C) 125 minutes
D) 501 minutes
E) 1000 minutes
 , a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 11 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 9 gallons per minute. At what time will the tank be full?
, a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 11 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 9 gallons per minute. At what time will the tank be full? A) 250 minutes
B) 126 minutes
C) 125 minutes
D) 501 minutes
E) 1000 minutes

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the differential equation. 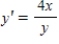
A)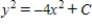
B)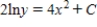
C)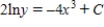
D)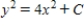
E)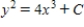
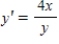
A)
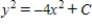
B)
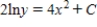
C)
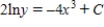
D)
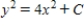
E)
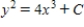

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
12
A 600-gallon tank is full of a solution containing 55 pounds of concentrate. Starting at time 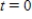 distilled water is added to the tank at a rate of 30 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the amount of concentrate Q in the solution as a function of t.
distilled water is added to the tank at a rate of 30 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the amount of concentrate Q in the solution as a function of t.
A)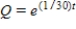
B)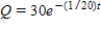
C)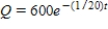
D)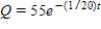
E)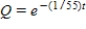
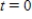 distilled water is added to the tank at a rate of 30 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the amount of concentrate Q in the solution as a function of t.
distilled water is added to the tank at a rate of 30 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the amount of concentrate Q in the solution as a function of t.A)
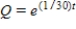
B)
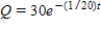
C)
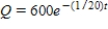
D)
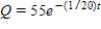
E)
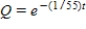

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
13
Find an equation of the graph that passes through the point 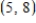 and has the slope
and has the slope 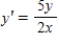 .
.
A)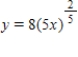
B)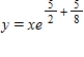
C)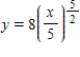
D)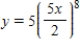
E)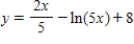
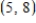 and has the slope
and has the slope 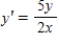 .
. A)
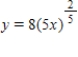
B)
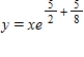
C)
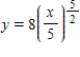
D)
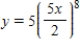
E)
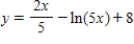

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
14
Solve the differential equation. 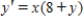
A)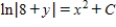
B)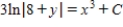
C)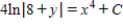
D)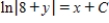
E)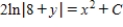
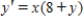
A)
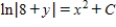
B)
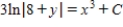
C)
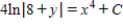
D)
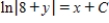
E)
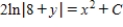

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
15
A conservation organization releases 30 panthers into a preserve. After 3 years, there are 50 panthers in the preserve. The preserve has a carrying capacity of 150. Determine the population after 6 years. Discard any fractional part of your answer.
A) 74
B) 66
C) 87
D) 79
E) 130
A) 74
B) 66
C) 87
D) 79
E) 130

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
16
Sketch the slope field for the differential equation 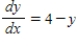 and use the slope field to sketch the solution satisfying the condition
and use the slope field to sketch the solution satisfying the condition 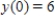 .
.
A)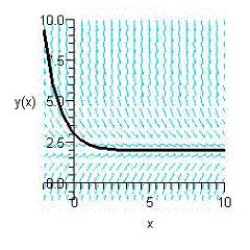
B)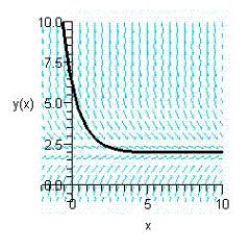
C)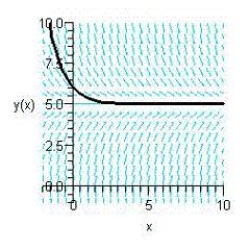
D)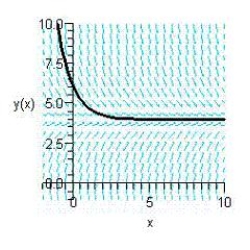
E)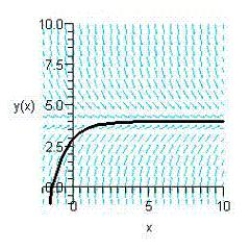
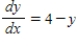 and use the slope field to sketch the solution satisfying the condition
and use the slope field to sketch the solution satisfying the condition 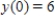 .
. A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
17
Solve the first order linear differential equation. 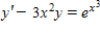
A)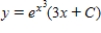
B)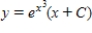
C)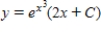
D)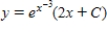
E)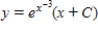
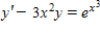
A)
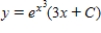
B)
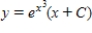
C)
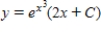
D)
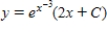
E)
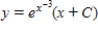

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
18
The logistic function 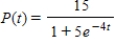 models the growth of a population. Determine when the population reaches
models the growth of a population. Determine when the population reaches 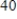 % of the maximum carrying capacity. Round your answer to three decimal places.
% of the maximum carrying capacity. Round your answer to three decimal places.
A) 4.317
B) 3.000
C) 0.474
D) 0.677
E) 0.301
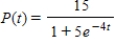 models the growth of a population. Determine when the population reaches
models the growth of a population. Determine when the population reaches 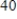 % of the maximum carrying capacity. Round your answer to three decimal places.
% of the maximum carrying capacity. Round your answer to three decimal places.A) 4.317
B) 3.000
C) 0.474
D) 0.677
E) 0.301

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
19
Find the particular solution of the differential equation 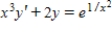 that satisfies the initial condition
that satisfies the initial condition 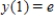 .
.
A)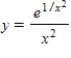
B)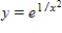
C)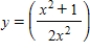
D)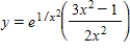
E)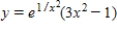
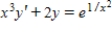 that satisfies the initial condition
that satisfies the initial condition 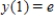 .
.A)
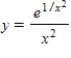
B)
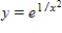
C)
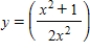
D)
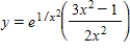
E)
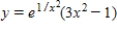

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
20
Find the principal that must be invested at the rate 6%, compounded monthly, so that $3,000,000 will be available for retirement in 55 years. Round your answer to the nearest cent.
A) $909,090.91
B) $111,563.08
C) $2,280,278.32
D) $825,000.00
E) $121,702.27
A) $909,090.91
B) $111,563.08
C) $2,280,278.32
D) $825,000.00
E) $121,702.27

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
21
A 200-gallon tank is full of a solution containing 25 pounds of concentrate. Starting at time 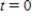 distilled water is added to the tank at a rate of 20 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the time at which the amount of concentrate in the tank reaches 15 pounds. Round your answer to one decimal place.
distilled water is added to the tank at a rate of 20 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the time at which the amount of concentrate in the tank reaches 15 pounds. Round your answer to one decimal place.
A) 2.2 min
B) 1.8 min
C) 10.2 min
D) 5.1 min
E) 10.2 min
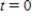 distilled water is added to the tank at a rate of 20 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the time at which the amount of concentrate in the tank reaches 15 pounds. Round your answer to one decimal place.
distilled water is added to the tank at a rate of 20 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the time at which the amount of concentrate in the tank reaches 15 pounds. Round your answer to one decimal place.A) 2.2 min
B) 1.8 min
C) 10.2 min
D) 5.1 min
E) 10.2 min

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
22
Sketch the slope field for the differential equation 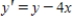 and use the slope field to sketch the solution that passes through the point
and use the slope field to sketch the solution that passes through the point 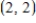 .
.
A)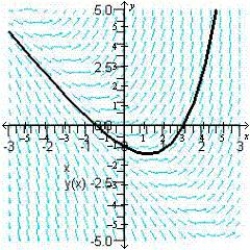
B)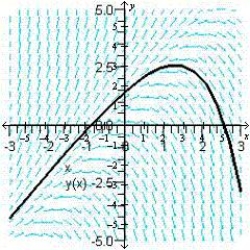
C)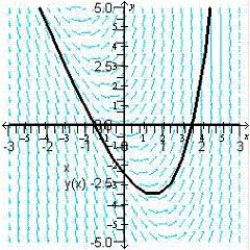
D)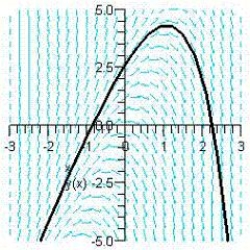
E)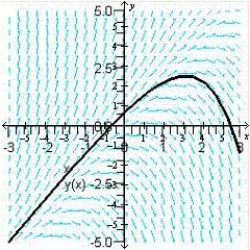
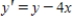 and use the slope field to sketch the solution that passes through the point
and use the slope field to sketch the solution that passes through the point 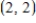 .
. A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
23
Find the particular solution of the differential equation 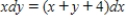 that satisfies the boundary condition
that satisfies the boundary condition 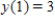 .
.
A)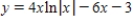
B)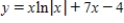
C)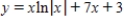
D)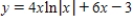
E)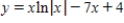
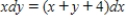 that satisfies the boundary condition
that satisfies the boundary condition 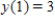 .
. A)
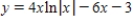
B)
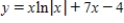
C)
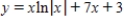
D)
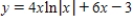
E)
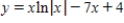

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
24
Find the orthogonal trajectories of the family 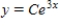 .
.
A)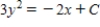
B)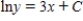
C)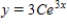
D)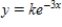
E)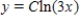
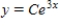 .
.
A)
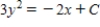
B)
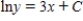
C)
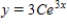
D)
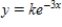
E)
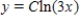

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
25
Use integration to find a general solution of the differential equation. 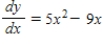
A)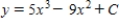
B)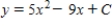
C)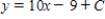
D)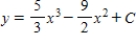
E)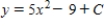
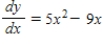
A)
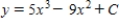
B)
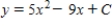
C)
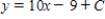
D)
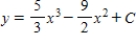
E)
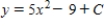

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
26
Find the particular solution of the differential equation 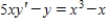 that satisfies the boundary condition
that satisfies the boundary condition 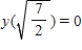 .
.
A)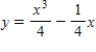
B)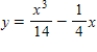
C)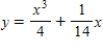
D)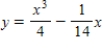
E)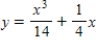
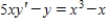 that satisfies the boundary condition
that satisfies the boundary condition 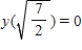 .
. A)
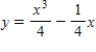
B)
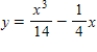
C)
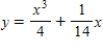
D)
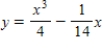
E)
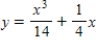

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
27
Select from the choices below the slope field for the differential equation. 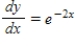
A)
B)
C)
D)
E) none of the above
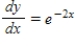
A)

B)

C)

D)

E) none of the above

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
28
Use integration to find a general solution of the differential equation. 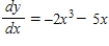
A)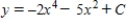
B)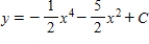
C)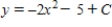
D)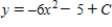
E)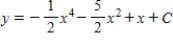
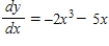
A)
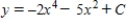
B)
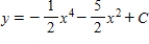
C)
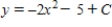
D)
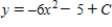
E)
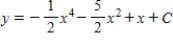

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
29
Identify the graph of the logistic function 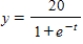 .
.
A)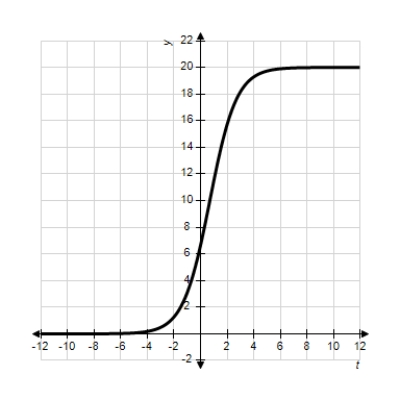
B)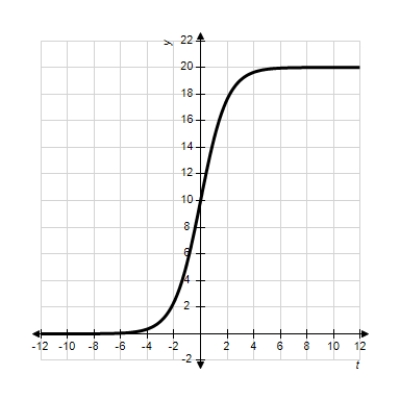
C)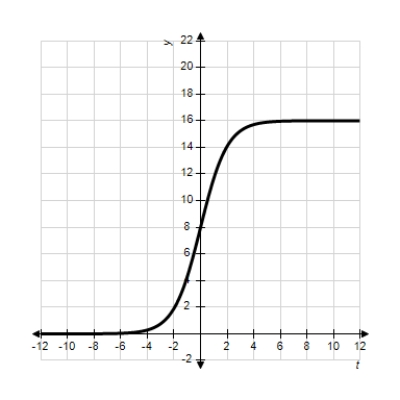
D)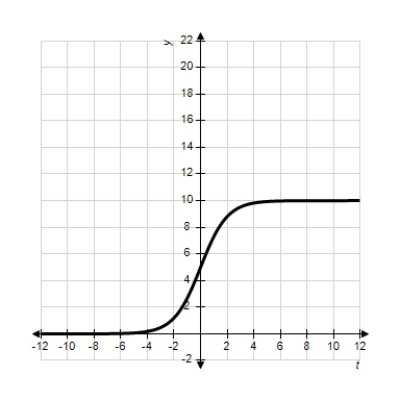
E)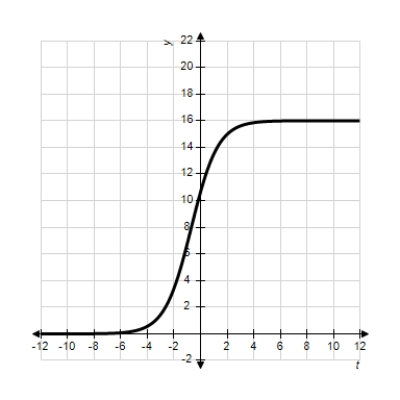
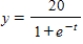 .
. A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
30
Match the logistic equation and initial condition with the graph of the solution. 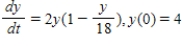
A)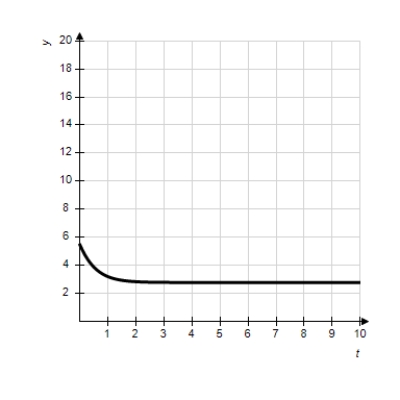
B)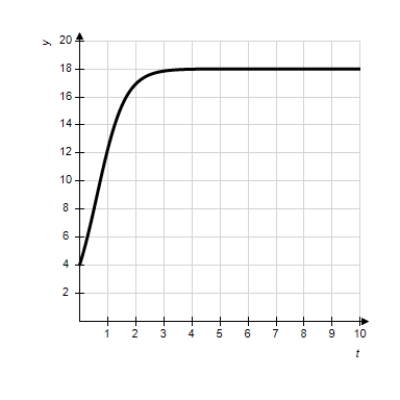
C)
D)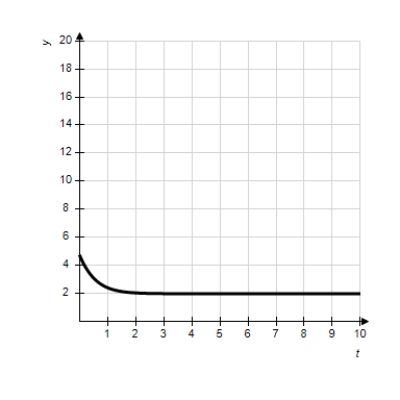
E)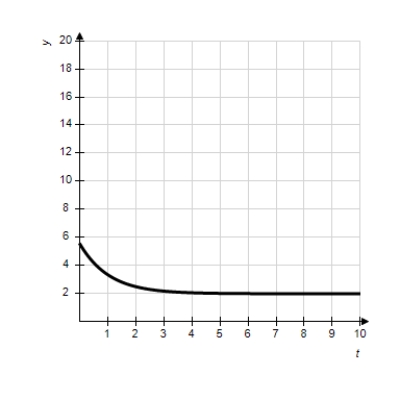
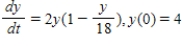
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
31
Sketch a few solutions of the differential equation on the slope field and then find the general solution analytically. 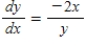
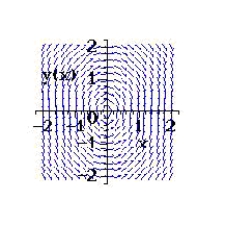
A)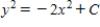
B)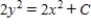
C)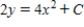
D)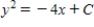
E)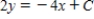
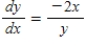

A)
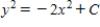
B)
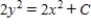
C)
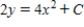
D)
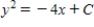
E)
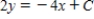

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
32
Suppose that the population (in millions) of a Uganda in 2007 is 30.3 and that expected continuous annual rate of change of the population is 0.036. The exponential growth model for the population by letting 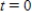 corresponds to 2000 is
corresponds to 2000 is 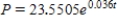 . Use the model to predict the population of the country in 2014. Round your answer to two decimal places.
. Use the model to predict the population of the country in 2014. Round your answer to two decimal places.
A) 32.56 millions
B) 37.61 millions
C) 40.41 millions
D) 38.98 millions
E) 31.41 millions
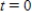 corresponds to 2000 is
corresponds to 2000 is 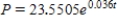 . Use the model to predict the population of the country in 2014. Round your answer to two decimal places.
. Use the model to predict the population of the country in 2014. Round your answer to two decimal places. A) 32.56 millions
B) 37.61 millions
C) 40.41 millions
D) 38.98 millions
E) 31.41 millions

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
33
The isotope 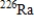 has a half-life of 1,599 years. After 20,000 years, a sample of the isotope is reduced 0.7 grams. What was the initial size of the sample (in grams)? How large was the sample after the first 2,000 years? Round your answers to four decimal places.
has a half-life of 1,599 years. After 20,000 years, a sample of the isotope is reduced 0.7 grams. What was the initial size of the sample (in grams)? How large was the sample after the first 2,000 years? Round your answers to four decimal places.
A) 4076.8643 g, 1713.1817 g
B) 5299.9236 g, 2227.1362 g
C) 2446.1186 g, 1027.9090 g
D) 3261.4914 g, 1370.5454 g
E) 2038.4321 g, 856.5909 g
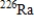 has a half-life of 1,599 years. After 20,000 years, a sample of the isotope is reduced 0.7 grams. What was the initial size of the sample (in grams)? How large was the sample after the first 2,000 years? Round your answers to four decimal places.
has a half-life of 1,599 years. After 20,000 years, a sample of the isotope is reduced 0.7 grams. What was the initial size of the sample (in grams)? How large was the sample after the first 2,000 years? Round your answers to four decimal places. A) 4076.8643 g, 1713.1817 g
B) 5299.9236 g, 2227.1362 g
C) 2446.1186 g, 1027.9090 g
D) 3261.4914 g, 1370.5454 g
E) 2038.4321 g, 856.5909 g

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
34
Find the exponential function 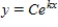 that passes through the two given points. Round your values of C and k to four decimal places.
that passes through the two given points. Round your values of C and k to four decimal places. 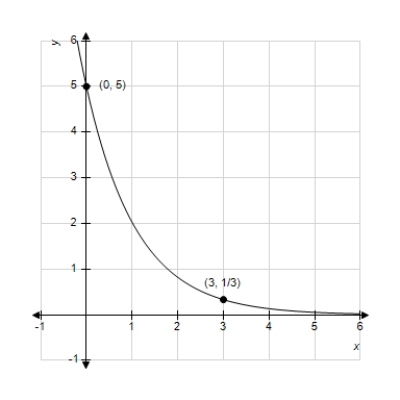
A)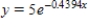
B)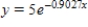
C)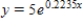
D)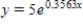
E)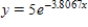
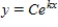 that passes through the two given points. Round your values of C and k to four decimal places.
that passes through the two given points. Round your values of C and k to four decimal places. 
A)
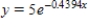
B)
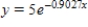
C)
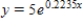
D)
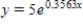
E)
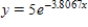

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
35
The logistic function 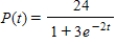 models the growth of a population. Identify the initial population.
models the growth of a population. Identify the initial population.
A) 6
B) 8
C) 3
D) 24
E) 2
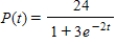 models the growth of a population. Identify the initial population.
models the growth of a population. Identify the initial population.A) 6
B) 8
C) 3
D) 24
E) 2

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
36
Use integration to find a general solution of the differential equation 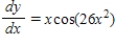
A)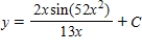
B)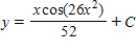
C)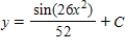
D)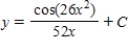
E)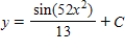
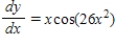
A)
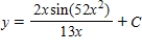
B)
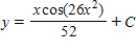
C)
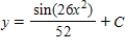
D)
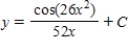
E)
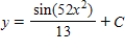

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
37
Which of the following is a solution of the differential equation 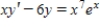 ?
?
A)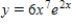
B)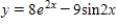
C)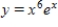
D)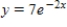
E)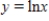
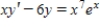 ?
? A)
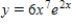
B)
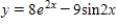
C)
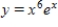
D)
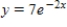
E)
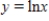

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
38
The logistic function 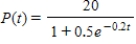 models the growth of a population. Identify the value of k.
models the growth of a population. Identify the value of k.
A) 1.7
B) 2.2
C) 0.2
D) 20
E) 0.5
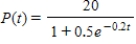 models the growth of a population. Identify the value of k.
models the growth of a population. Identify the value of k.A) 1.7
B) 2.2
C) 0.2
D) 20
E) 0.5

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the differential equation 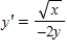 .
.
A)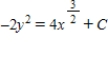
B)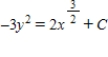
C)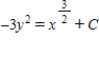
D)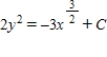
E)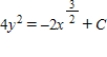
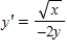 .
. A)
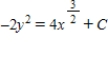
B)
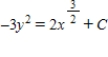
C)
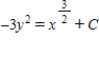
D)
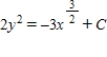
E)
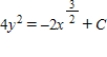

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
40
Use integration to find a general solution of the differential equation . 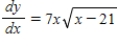
A)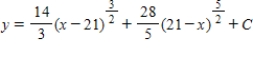
B)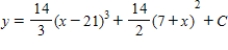
C)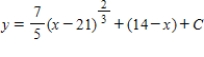
D)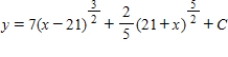
E)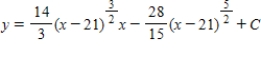
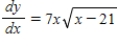
A)
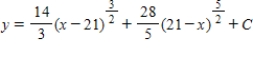
B)
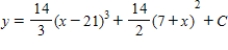
C)
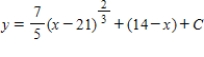
D)
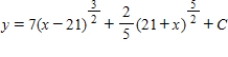
E)
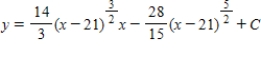

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the Bernoulli differential equation 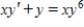 .
.
A)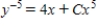
B)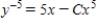
C)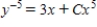
D)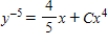
E)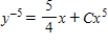
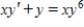 .
.A)
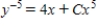
B)
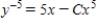
C)
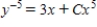
D)
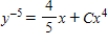
E)
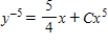

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
42
Sketch a few solutions of the differential equation on the slope field and then find the general solution analytically. 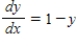
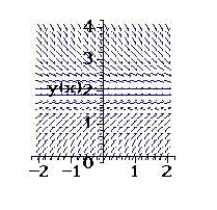
A)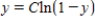
B)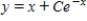
C)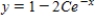
D)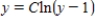
E)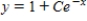
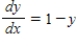

A)
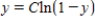
B)
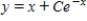
C)
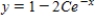
D)
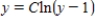
E)
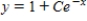

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
43
Suppose that the population (in millions) of Hungary in 2007 was 10 and that the expected continuous annual rate of change of the population is -0.003. Find the exponential growth model 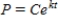 for the population by letting
for the population by letting 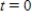 correspond to 2000. Round your answer to four decimal places.
correspond to 2000. Round your answer to four decimal places.
A)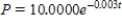
B)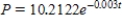
C)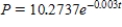
D)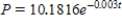
E)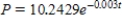
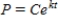 for the population by letting
for the population by letting 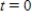 correspond to 2000. Round your answer to four decimal places.
correspond to 2000. Round your answer to four decimal places. A)
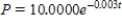
B)
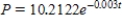
C)
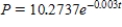
D)
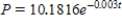
E)
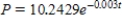

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
44
Find the time (in years) necessary for 1,000 to double if it is invested at a rate 6% compounded continuously. Round your answer to two decimal places.
A) 1.16 years
B) 11.55 years
C) 1.39 years
D) 11.90 years
E) 11.58 years
A) 1.16 years
B) 11.55 years
C) 1.39 years
D) 11.90 years
E) 11.58 years

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
45
The initial investment in a savings account in which interest is compounded continuously is $803. If the time required to double the amount is 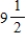 years, what is the annual rate? Round your answer to two decimal places.
years, what is the annual rate? Round your answer to two decimal places.
A) 7.30 %
B) 7.70 %
C) 13.71 %
D) 6.10 %
E) 8.70 %
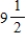 years, what is the annual rate? Round your answer to two decimal places.
years, what is the annual rate? Round your answer to two decimal places. A) 7.30 %
B) 7.70 %
C) 13.71 %
D) 6.10 %
E) 8.70 %

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
46
Use integration to find a general solution of the differential equation. 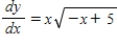
A)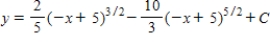
B)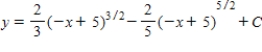
C)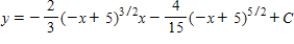
D)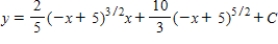
E)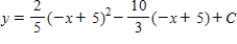
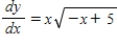
A)
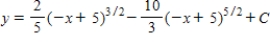
B)
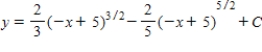
C)
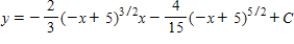
D)
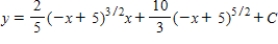
E)
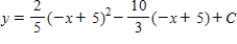

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
47
Assume an object weighing 7 pounds is dropped from a height of 9,000 feet, where the air resistance is proportional to the velocity. Round numerical answers in your answer to two places.
(i) Write the velocity as a function of time if the object's velocity after 4 seconds is 2.33 feet per second.
(ii) What is the limiting value of the velocity function?
A) (i)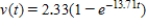 ; (ii) 0
; (ii) 0
B) (i)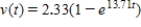 ; (ii) 0
; (ii) 0
C) (i)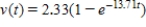 ; (ii) 2.33
; (ii) 2.33
D) (i)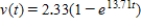 ; (ii) 2.33
; (ii) 2.33
E) (i)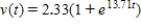 ; (ii) limit does not exist
; (ii) limit does not exist
(i) Write the velocity as a function of time if the object's velocity after 4 seconds is 2.33 feet per second.
(ii) What is the limiting value of the velocity function?
A) (i)
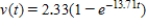 ; (ii) 0
; (ii) 0B) (i)
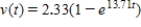 ; (ii) 0
; (ii) 0C) (i)
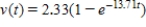 ; (ii) 2.33
; (ii) 2.33D) (i)
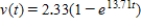 ; (ii) 2.33
; (ii) 2.33E) (i)
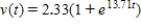 ; (ii) limit does not exist
; (ii) limit does not exist
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
48
Find an equation of the graph that passes through the point 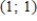 and has the slope
and has the slope 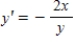 .
.
A)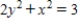
B)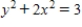
C)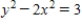
D)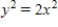
E)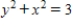
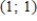 and has the slope
and has the slope 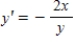 .
. A)
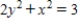
B)
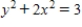
C)
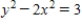
D)
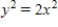
E)
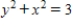

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
49
Find the function 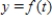 passing through the point
passing through the point 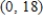 with the first derivative
with the first derivative 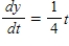 .
.
A)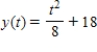
B)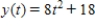
C)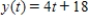
D)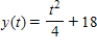
E)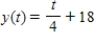
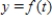 passing through the point
passing through the point 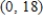 with the first derivative
with the first derivative 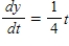 .
. A)
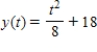
B)
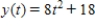
C)
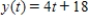
D)
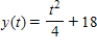
E)
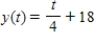

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
50
Use Euler's Method to make a table of values for the approximate solution of the following differential equation with specified initial value. Use 5 steps of size 0.05. 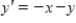 ,
, 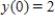
A) 
0)000
1)000
2)000
3)000
4)000
5)000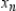
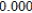
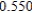
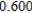
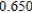
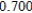
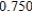
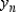
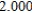
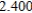
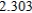
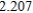
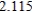
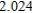
B) 
0)000
1)000
2)000
3)000
4)000
5)000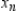
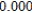
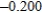
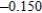
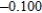
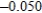
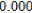
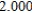
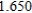
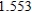
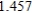
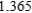
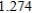
C) 
0)000
1)000
2)000
3)000
4)000
5)000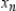
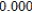
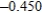
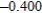
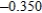
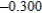
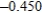
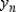
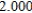
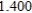
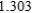
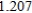
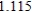
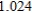
D) 
0)000
1)000
2)000
3)000
4)000
5)000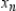
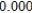
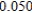
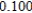
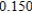
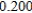
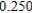
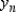
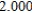
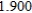
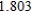
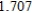
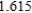
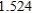
E) 
0)000
1)000
2)000
3)000
4)000
5)000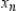
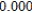
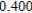
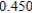
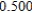
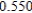
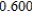
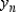
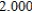
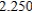
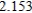
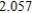
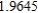
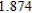
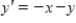 ,
, 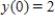
A)

0)000
1)000
2)000
3)000
4)000
5)000
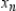
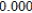
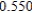
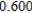
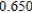
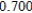
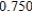
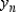
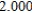
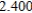
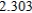
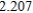
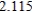
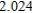
B)

0)000
1)000
2)000
3)000
4)000
5)000
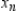
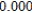
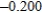
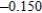
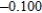
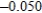
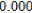
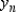
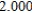
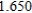
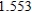
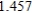
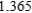
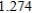
C)

0)000
1)000
2)000
3)000
4)000
5)000
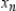
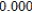
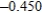
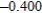
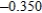
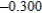
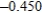
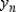
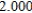
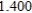
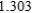
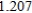
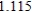
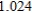
D)

0)000
1)000
2)000
3)000
4)000
5)000
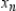
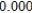
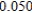
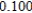
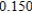
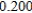
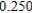
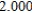
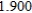
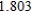
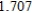
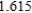
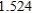
E)

0)000
1)000
2)000
3)000
4)000
5)000
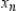
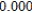
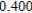
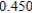
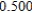
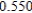
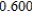
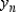
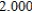
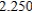
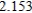
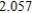
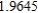
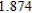

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
51
Find the logistic equation that satisfies the following differential equation and initial condition. 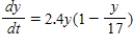 ,
, 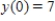
A)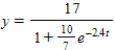
B)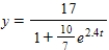
C)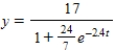
D)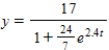
E) none of these
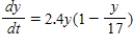 ,
, 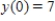
A)
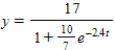
B)
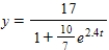
C)
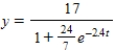
D)
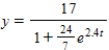
E) none of these

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
52
A calf that weighs 75 pounds at birth gains weight at the rate 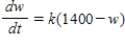 where w is weight in pounds and t is time in years. If the animal is sold when its weight reaches 900 pounds, find the time of sale using the model
where w is weight in pounds and t is time in years. If the animal is sold when its weight reaches 900 pounds, find the time of sale using the model 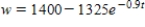 . Round your answer to two decimal places.
. Round your answer to two decimal places.
A) 7.02 years
B) 2.76 years
C) 1.12 years
D) 1.08 years
E) 0.44 year
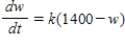 where w is weight in pounds and t is time in years. If the animal is sold when its weight reaches 900 pounds, find the time of sale using the model
where w is weight in pounds and t is time in years. If the animal is sold when its weight reaches 900 pounds, find the time of sale using the model 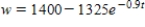 . Round your answer to two decimal places.
. Round your answer to two decimal places. A) 7.02 years
B) 2.76 years
C) 1.12 years
D) 1.08 years
E) 0.44 year

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
53
Solve the differential equation. 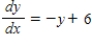
A)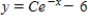
B)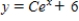
C)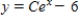
D)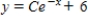
E)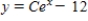
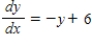
A)
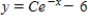
B)
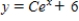
C)
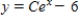
D)
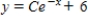
E)
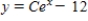

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
54
A conservation organization releases 20 wolves into a preserve. After 2 years, there are 35 wolves in the preserve. The preserve has a carrying capacity of 125. Determine the time it takes for the population to reach 80.
A) 9.020 years
B) 4.875 years
C) 6.259 years
D) 3.692 years
E) 7.884 years
A) 9.020 years
B) 4.875 years
C) 6.259 years
D) 3.692 years
E) 7.884 years

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
55
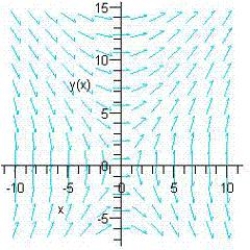
Use the differential equation 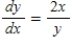 and its slope field to find the slope at the point
and its slope field to find the slope at the point 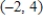 .
. 
A) -8
B) -1
C) -4
D) -16
E) 8
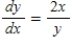 and its slope field to find the slope at the point
and its slope field to find the slope at the point 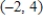 .
. 
A) -8
B) -1
C) -4
D) -16
E) 8

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
56
Select from the choices below the slope field for the differential equation. 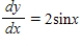
A)
B)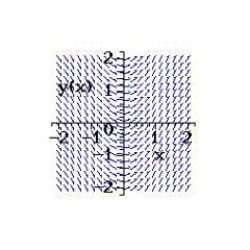
C)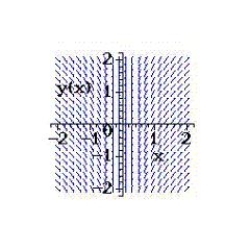
D) none of the above
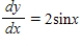
A)

B)

C)

D) none of the above

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
57
Find the particular solution of the differential equation 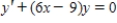 that satisfies the boundary condition
that satisfies the boundary condition 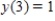 .
.
A)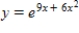
B)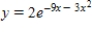
C)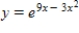
D)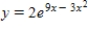
E)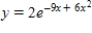
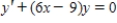 that satisfies the boundary condition
that satisfies the boundary condition 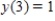 .
. A)
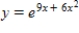
B)
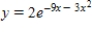
C)
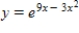
D)
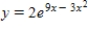
E)
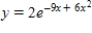

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
58
Match the logistic differential equation and initial condition with the graph of its solution shown below. 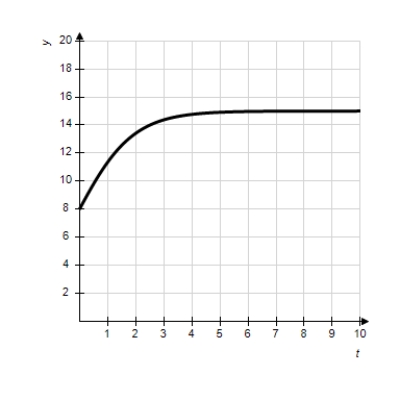
A)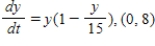
B)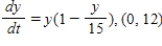
C)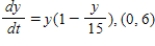
D)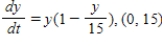
E)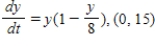

A)
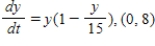
B)
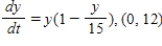
C)
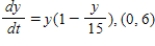
D)
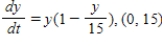
E)
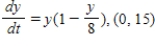

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
59
A 300-gallon tank is half full of distilled water. At time 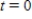 , a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 6 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 4 gallons per minute. At the time the tank is full, how many pounds of concentrate will it contain? Round your answer to two decimal places.
, a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 6 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 4 gallons per minute. At the time the tank is full, how many pounds of concentrate will it contain? Round your answer to two decimal places.
A)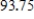 lbs
lbs
B)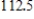 lbs
lbs
C)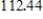 lbs
lbs
D)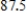 lbs
lbs
E)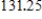 lbs
lbs
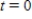 , a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 6 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 4 gallons per minute. At the time the tank is full, how many pounds of concentrate will it contain? Round your answer to two decimal places.
, a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 6 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 4 gallons per minute. At the time the tank is full, how many pounds of concentrate will it contain? Round your answer to two decimal places.A)
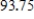 lbs
lbsB)
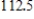 lbs
lbsC)
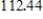 lbs
lbsD)
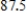 lbs
lbsE)
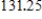 lbs
lbs
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the first order linear differential equation. 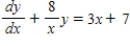
A)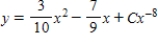
B)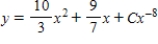
C)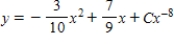
D)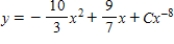
E)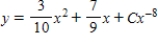
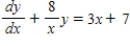
A)
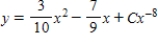
B)
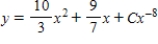
C)
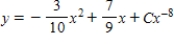
D)
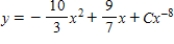
E)
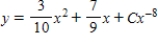

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
61
Find the orthogonal trajectories of the family 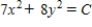 .
.
A)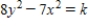
B)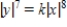
C)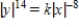
D)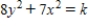
E)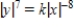
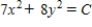 .
. A)
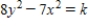
B)
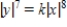
C)
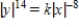
D)
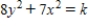
E)
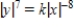

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
62
The number of bacteria in a culture is increasing according to the law of exponential growth. After 2 hours there are 135 bacteria in the culture and after 4 hours there are 390 bacteria in the culture. Answer the following questions, rounding numerical answers to four decimal places.
(i) Find the initial population.
(ii) Write an exponential growth model for the bacteria population. Let t represent time in hours.
(iii) Use the model to determine the number of bacteria after 8 hours.
(iv) After how many hours will the bacteria count be 25,000?
A) (i) 46.7341; (ii)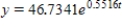 ; (iii) 4,566.8441; (iv) 14.1787 hr
; (iii) 4,566.8441; (iv) 14.1787 hr
B) (i) 48.8841; (ii)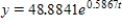 ; (iii) 5,941.5613; (iv) 16.4067 hr
; (iii) 5,941.5613; (iv) 16.4067 hr
C) (i) 46.7341; (ii)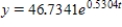 ; (iii) 3,254.11; (iv) 11.8442 hr
; (iii) 3,254.11; (iv) 11.8442 hr
D) (i) 52.5141; (ii)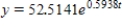 ; (iii) 8,693.0147; (iv) 18.5179hr
; (iii) 8,693.0147; (iv) 18.5179hr
E) (i) 54.0741; (ii)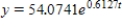 ; (iii) 11,345.4782; (iv) 20.2973 hr
; (iii) 11,345.4782; (iv) 20.2973 hr
(i) Find the initial population.
(ii) Write an exponential growth model for the bacteria population. Let t represent time in hours.
(iii) Use the model to determine the number of bacteria after 8 hours.
(iv) After how many hours will the bacteria count be 25,000?
A) (i) 46.7341; (ii)
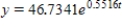 ; (iii) 4,566.8441; (iv) 14.1787 hr
; (iii) 4,566.8441; (iv) 14.1787 hrB) (i) 48.8841; (ii)
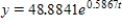 ; (iii) 5,941.5613; (iv) 16.4067 hr
; (iii) 5,941.5613; (iv) 16.4067 hrC) (i) 46.7341; (ii)
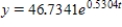 ; (iii) 3,254.11; (iv) 11.8442 hr
; (iii) 3,254.11; (iv) 11.8442 hrD) (i) 52.5141; (ii)
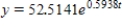 ; (iii) 8,693.0147; (iv) 18.5179hr
; (iii) 8,693.0147; (iv) 18.5179hrE) (i) 54.0741; (ii)
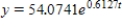 ; (iii) 11,345.4782; (iv) 20.2973 hr
; (iii) 11,345.4782; (iv) 20.2973 hr
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
63
Use integration to find a general solution of the differential equation. 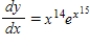
A)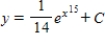
B)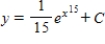
C)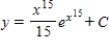
D)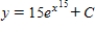
E)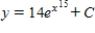
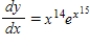
A)
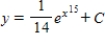
B)
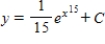
C)
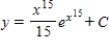
D)
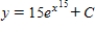
E)
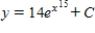

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
64
Find the general solution of the differential equation 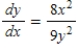 .
.
A)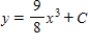
B)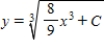
C)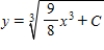
D)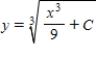
E)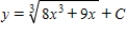
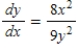 .
. A)
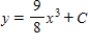
B)
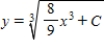
C)
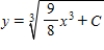
D)
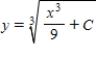
E)
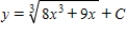

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
65
A 300-gallon tank is full of a solution containing 55 pounds of concentrate. Starting at time 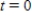 distilled water is added to the tank at a rate of 30 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the quantity of the concentrate in the solution as
distilled water is added to the tank at a rate of 30 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the quantity of the concentrate in the solution as 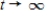 .
.
A) 30
B) 56
C) 55
D) 0
E) 1
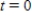 distilled water is added to the tank at a rate of 30 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the quantity of the concentrate in the solution as
distilled water is added to the tank at a rate of 30 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the quantity of the concentrate in the solution as 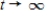 .
. A) 30
B) 56
C) 55
D) 0
E) 1

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
66
The initial investment in a savings account in which interest is compounded continuously is $768. If the time required to double the amount is 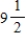 years, what is the amount after 13 years? Round your answer to the nearest cent.
years, what is the amount after 13 years? Round your answer to the nearest cent.
A) $2,090.17
B) $1,982.88
C) $2,101.89
D) $1,582.88
E) $10,525.90
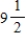 years, what is the amount after 13 years? Round your answer to the nearest cent.
years, what is the amount after 13 years? Round your answer to the nearest cent. A) $2,090.17
B) $1,982.88
C) $2,101.89
D) $1,582.88
E) $10,525.90

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
67
The isotope 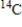 has a half-life of 5,715 years. After 2,000 years, a sample of the isotope is reduced to 2.1 grams. What was the initial size of the sample (in grams)? How much will remain after 20,000 years (i.e., after another 18,000 years)? Round your answers to four decimal places.
has a half-life of 5,715 years. After 2,000 years, a sample of the isotope is reduced to 2.1 grams. What was the initial size of the sample (in grams)? How much will remain after 20,000 years (i.e., after another 18,000 years)? Round your answers to four decimal places.
A) 1.8735 g, 0.1656 g
B) 4.2824 g, 0.3786 g
C) 2.6765 g, 0.2366 g
D) 3.7471 g, 0.3313 g
E) 3.4794 g, 0.3076 g
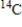 has a half-life of 5,715 years. After 2,000 years, a sample of the isotope is reduced to 2.1 grams. What was the initial size of the sample (in grams)? How much will remain after 20,000 years (i.e., after another 18,000 years)? Round your answers to four decimal places.
has a half-life of 5,715 years. After 2,000 years, a sample of the isotope is reduced to 2.1 grams. What was the initial size of the sample (in grams)? How much will remain after 20,000 years (i.e., after another 18,000 years)? Round your answers to four decimal places. A) 1.8735 g, 0.1656 g
B) 4.2824 g, 0.3786 g
C) 2.6765 g, 0.2366 g
D) 3.7471 g, 0.3313 g
E) 3.4794 g, 0.3076 g

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
68
The logistic function 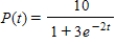 models the growth of a population. Identify the maximum carrying capacity.
models the growth of a population. Identify the maximum carrying capacity.
A) 10
B) 3.5
C) 3
D) 2
E) 4
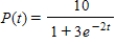 models the growth of a population. Identify the maximum carrying capacity.
models the growth of a population. Identify the maximum carrying capacity.A) 10
B) 3.5
C) 3
D) 2
E) 4

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
69
A calf that weighs 70 pounds at birth gains weight at the rate 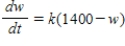 where w is weight in pounds and t is time in years. Use a computer algebra system to solve the differential equation for
where w is weight in pounds and t is time in years. Use a computer algebra system to solve the differential equation for 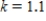 .
.
A)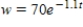
B)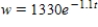
C)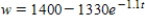
D)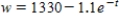
E)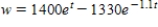
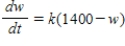 where w is weight in pounds and t is time in years. Use a computer algebra system to solve the differential equation for
where w is weight in pounds and t is time in years. Use a computer algebra system to solve the differential equation for 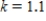 .
. A)
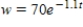
B)
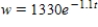
C)
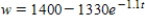
D)
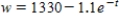
E)
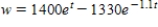

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
70
A conservation organization releases 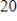
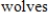 into a preserve. After
into a preserve. After  years, there are
years, there are 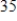
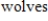 in the preserve. The preserve has a carrying capacity of
in the preserve. The preserve has a carrying capacity of 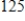 . Write a logistic function that models the population of
. Write a logistic function that models the population of 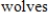 in the preserve.
in the preserve.
A)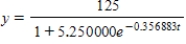
B)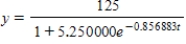
C)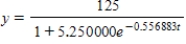
D)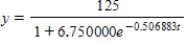
E)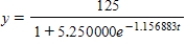
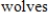 into a preserve. After
into a preserve. After  years, there are
years, there are 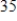
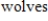 in the preserve. The preserve has a carrying capacity of
in the preserve. The preserve has a carrying capacity of 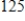 . Write a logistic function that models the population of
. Write a logistic function that models the population of  in the preserve.
in the preserve.A)
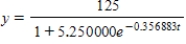
B)
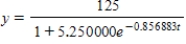
C)
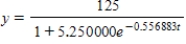
D)
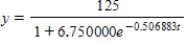
E)
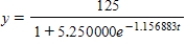

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
71
Select from the choices below the slope field for the differential equation. 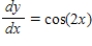
A)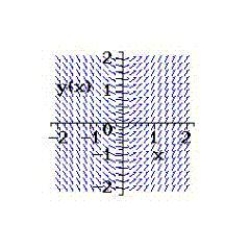
B)
C)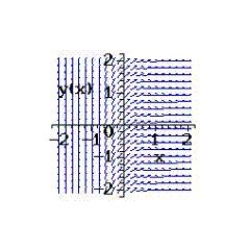
D)
E) none of the above
A)

B)

C)

D)

E) none of the above

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
72
Use  as a integrating factor to find the general solution of the differential equation
as a integrating factor to find the general solution of the differential equation  .
.
A)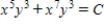
B)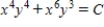
C)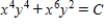
D)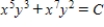
E)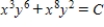
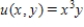 as a integrating factor to find the general solution of the differential equation
as a integrating factor to find the general solution of the differential equation 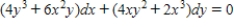 .
. A)
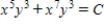
B)
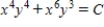
C)
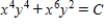
D)
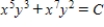
E)
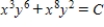

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
73
Find the particular solution of the differential equation 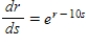 that satisfies the initial condition
that satisfies the initial condition 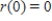 .
.
A)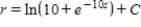
B)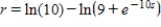
C)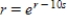
D)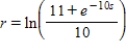
E)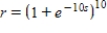
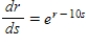 that satisfies the initial condition
that satisfies the initial condition 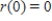 .
. A)
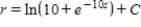
B)
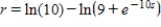
C)
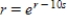
D)
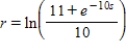
E)
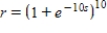

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
74
Find the general solution of the differential equation. 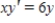
A)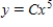
B)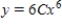
C)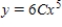
D)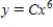
E)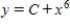
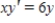
A)
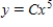
B)
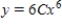
C)
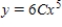
D)
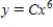
E)
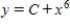

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
75
The half-life of the carbon isotope C-14 is approximately 5,715 years. If the amount left after 4,000 years is 1.3 g, what is the amount after 8,000 years? Round your answer to three decimal places.
A) 0.800 g
B) 0.628 g
C) 1.300 g
D) 0.303 g
E) 1.601 g
A) 0.800 g
B) 0.628 g
C) 1.300 g
D) 0.303 g
E) 1.601 g

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
76
A phase trajectory is shown for populations of rabbits and foxes. Describe how each population changes as time goes by. 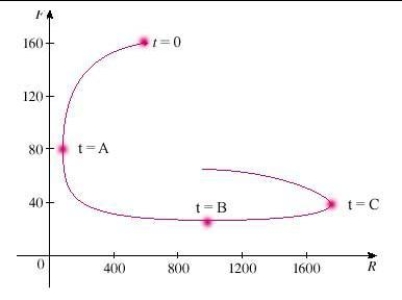
Select the correct statement.
A) At the population of foxes reaches a minimum of about 30.
the population of foxes reaches a minimum of about 30.
B) At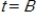 the number of rabbits rebounds to 500.
the number of rabbits rebounds to 500.
C) At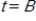 the number of foxes reaches a maximum of about 2400.
the number of foxes reaches a maximum of about 2400.

Select the correct statement.
A) At
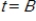 the population of foxes reaches a minimum of about 30.
the population of foxes reaches a minimum of about 30.B) At
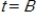 the number of rabbits rebounds to 500.
the number of rabbits rebounds to 500.C) At
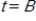 the number of foxes reaches a maximum of about 2400.
the number of foxes reaches a maximum of about 2400.
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
77
Write and solve the differential equation that models the following verbal statement:
The rate of change of with respect to
with respect to  is proportional to
is proportional to 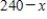 .
.
A)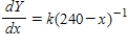 ,
, 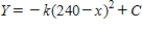
B)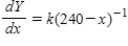 ,
, 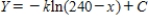
C)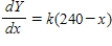 ,
, 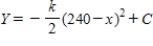
D)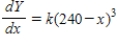 ,
, 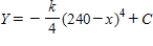
E)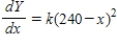 ,
, 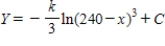
The rate of change of
 with respect to
with respect to  is proportional to
is proportional to 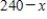 .
.
A)
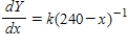 ,
, 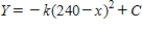
B)
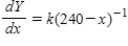 ,
, 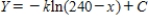
C)
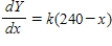 ,
, 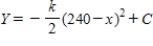
D)
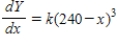 ,
, 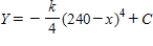
E)
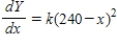 ,
, 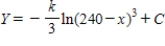

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
78
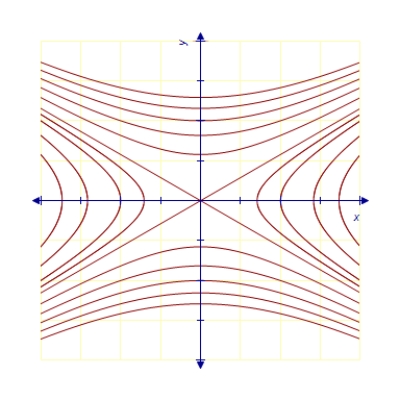
Find the orthogonal trajectories of the family 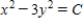 .
. 
A)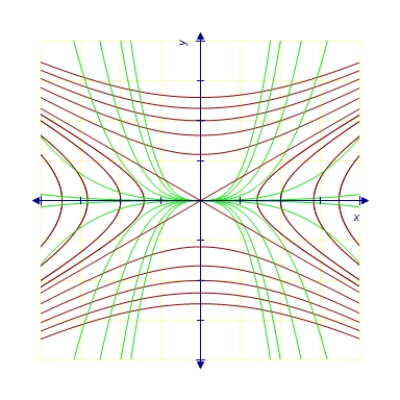
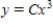
B)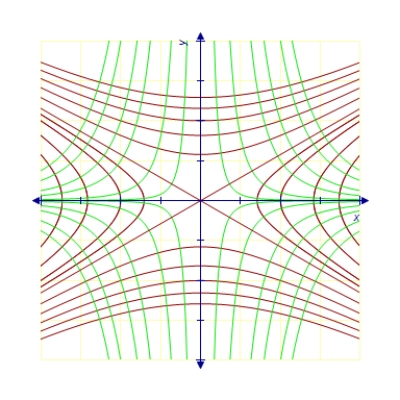
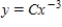
C)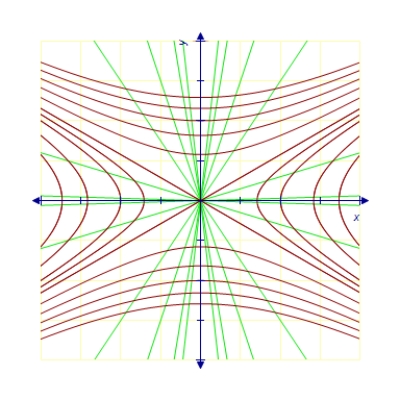
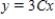
D)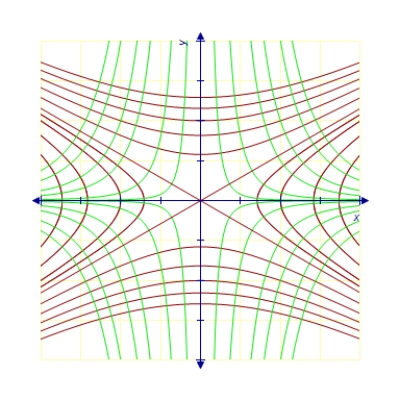
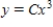
E)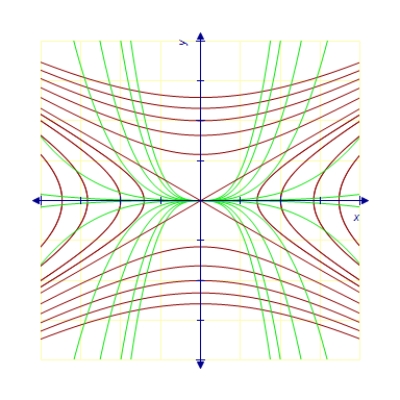
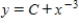
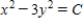 .
. 
A)

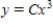
B)

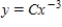
C)

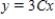
D)

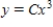
E)

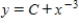

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
79
Each of the following graphs is from a logistic function 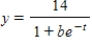 . Which one has the smallest value of b?
. Which one has the smallest value of b?
A)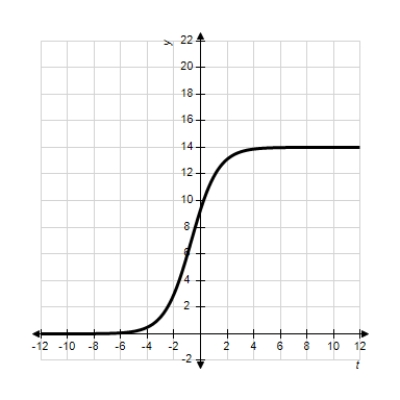
B)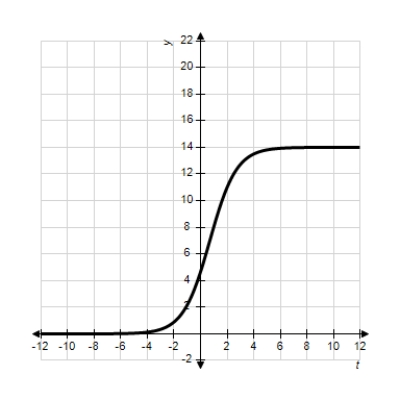
C)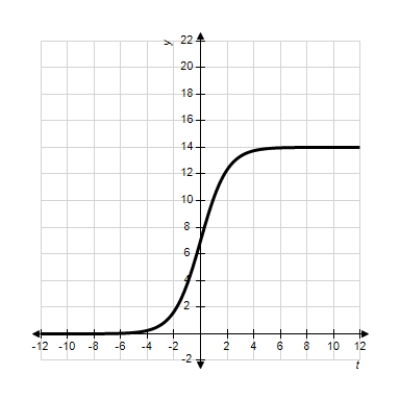
D)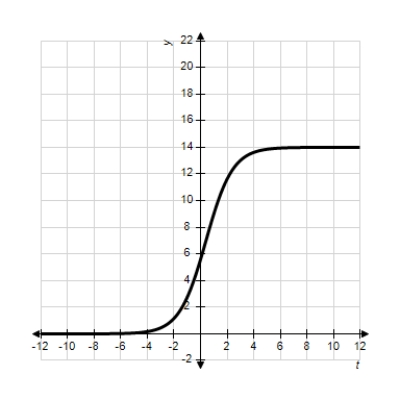
E)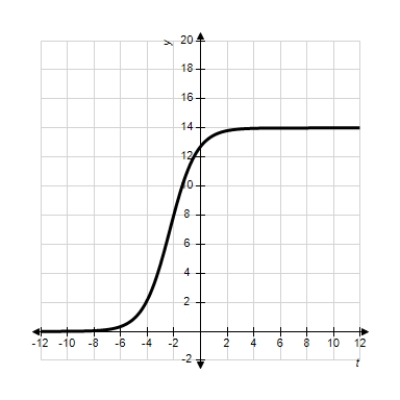
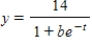 . Which one has the smallest value of b?
. Which one has the smallest value of b? A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
80
Suppose an eight-pound object is dropped from a height of 5,000 feet, where the air resistance is proportional to the velocity. Write the velocity as a function of time if its velocity after 4 seconds is approximately -50 feet per second. Use a graphing utility or a computer algebra system. Round numerical answers in your answer to four places.
A)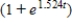
B)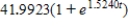
C)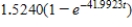
D)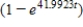
E)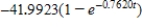
A)
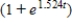
B)
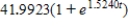
C)
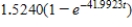
D)
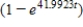
E)
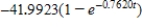

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck


