Deck 14: Iterated Integrals and Area in the Plane
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/118
Play
Full screen (f)
Deck 14: Iterated Integrals and Area in the Plane
1
 order of integration and show that both orders yield the same area. What is this area?
order of integration and show that both orders yield the same area. What is this area? 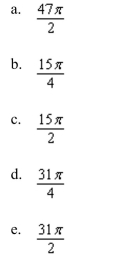
C
2
Evaluate the following iterated integral. 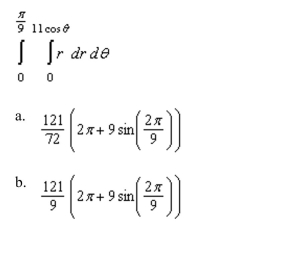
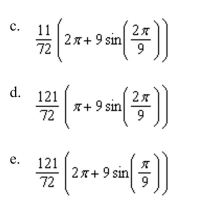
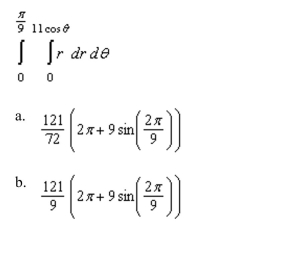
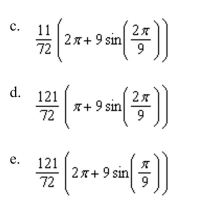
A
3
an iterated integral to find the area of the region bounded by 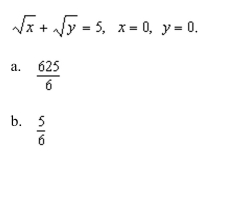

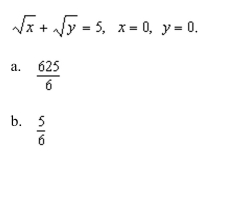

A
4
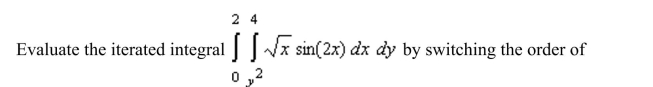 integration. Round your answer to three decimal places.
integration. Round your answer to three decimal places. 

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
5
Evaluate the following iterated integral. 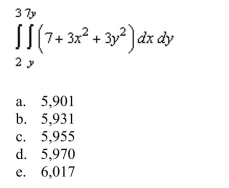
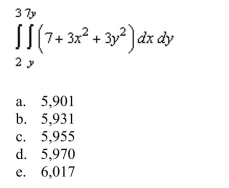

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
6
Evaluate the following integral. 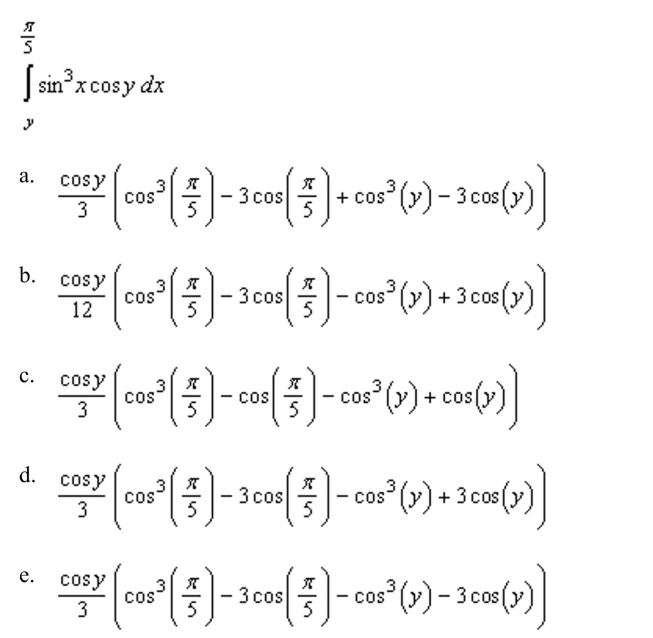
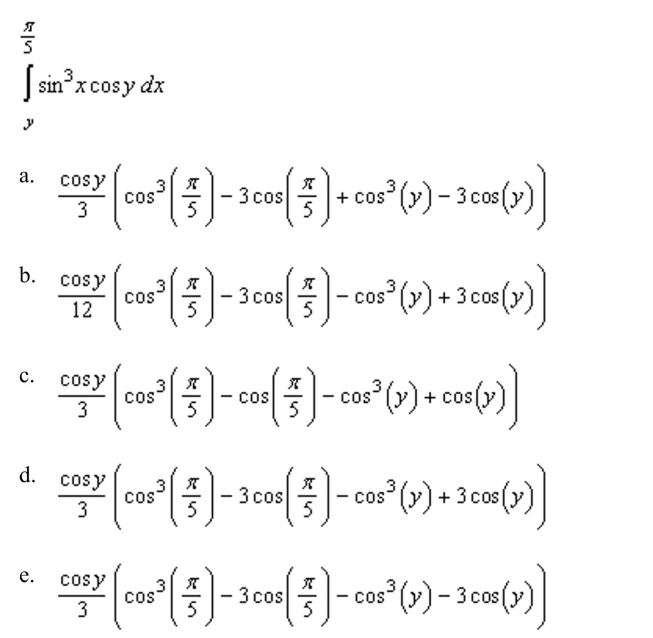

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
7
Sketch the region R of integration and then switch the order of integration for the following integral. 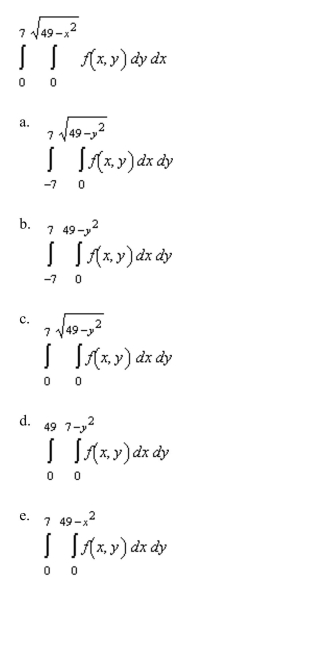
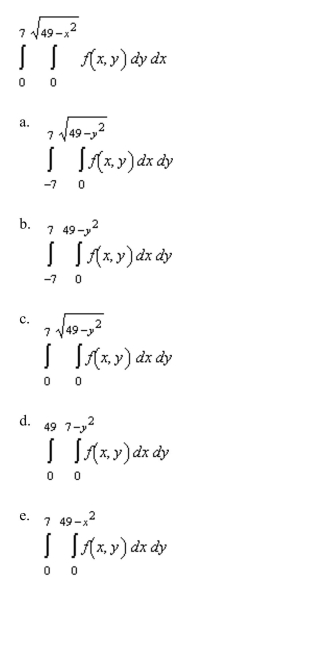

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
8
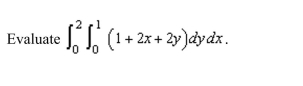
A)3
B)8
C)6
D)9
E)5

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
9
an iterated integral to find the area of the region bounded by the graphs of the equations 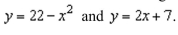

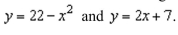


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate the following integral. 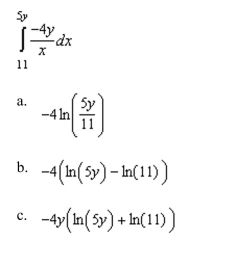
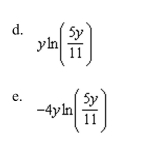
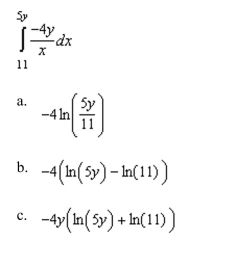
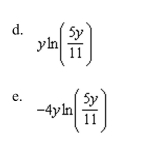

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
11
Evaluate the following iterated integral. 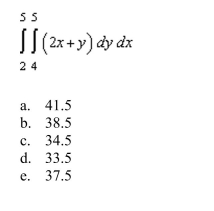
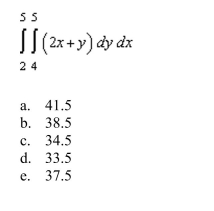

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
12
Evaluate the following integral. 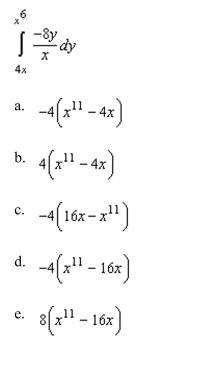
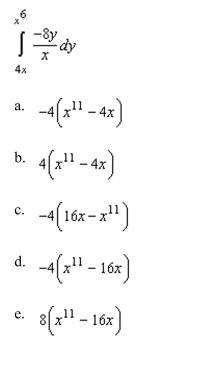

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
13
Evaluate the following iterated integral. 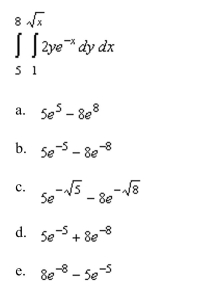
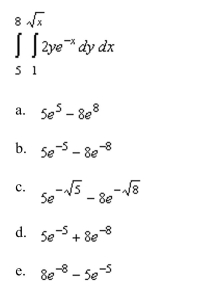

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
14
Evaluate the following improper integral. 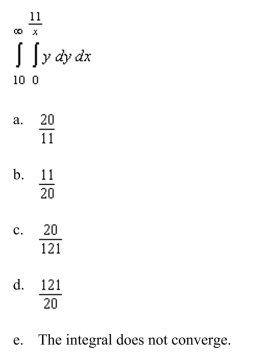
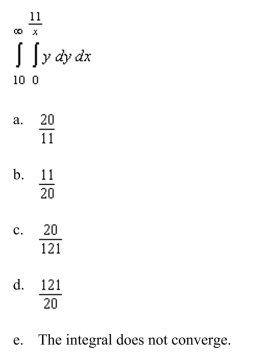

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
15
an iterated integral to find the area of the region shown in the figure below. 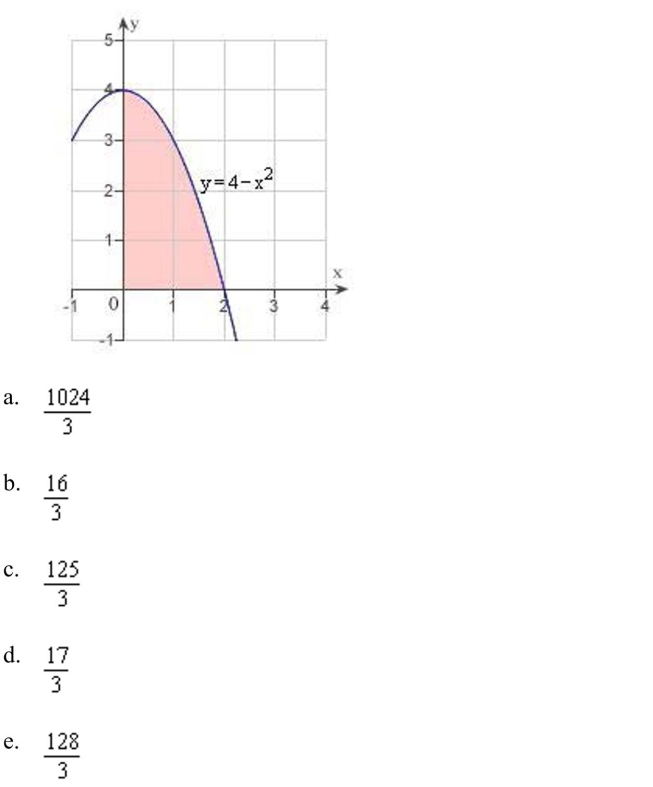


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
16
Evaluate the iterated integral below. Note that it is necessary to switch the order of integration. 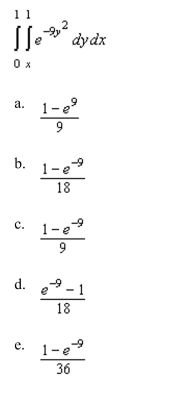
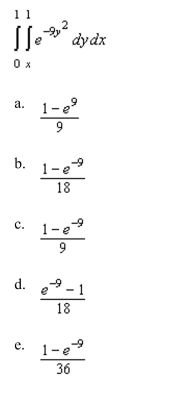

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
17
 of integration and show that both orders yield the same area. What is this area?
of integration and show that both orders yield the same area. What is this area? 

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
18
area of a region R is given by the iterated integrals 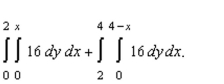 Switch the order of integration and show that both orders yield the same area. What is this area?
Switch the order of integration and show that both orders yield the same area. What is this area? 
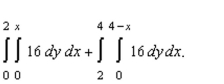 Switch the order of integration and show that both orders yield the same area. What is this area?
Switch the order of integration and show that both orders yield the same area. What is this area? 

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
19

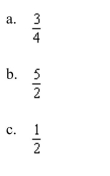
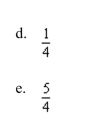

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
20
an iterated integral to find the area of the region bounded by 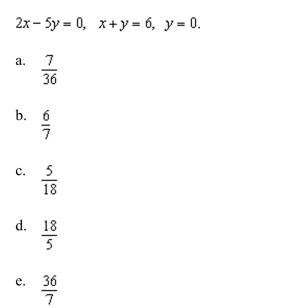
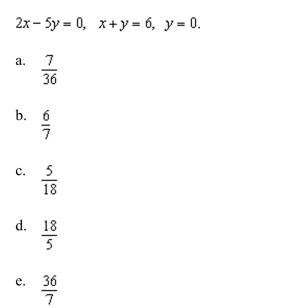

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
21
Suppose the temperature in degrees Celsius on the surface of a metal plate is 


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
22
up and evaluate a double integral to find the volume of the solid bounded by the graphs of the equations 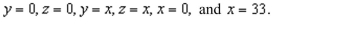
A)1,089
B)35,937
C)35,949
D)11,979
E)2,178
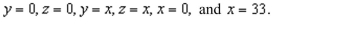
A)1,089
B)35,937
C)35,949
D)11,979
E)2,178

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
23
a double integral to find the volume of the indicated solid. 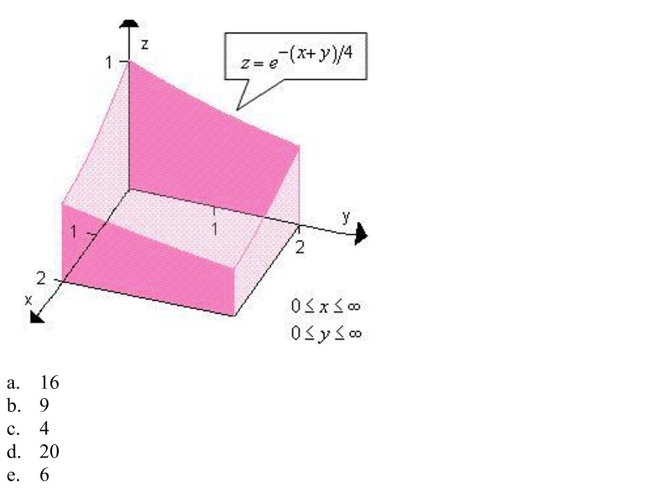


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
24
Evaluate the double integral below. 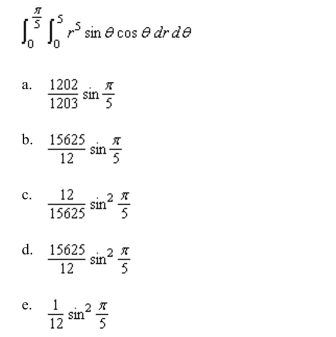
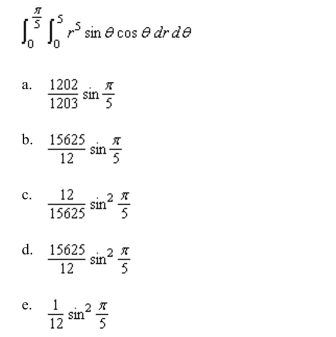

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
25
Combine the sum of the two iterated integrals into a single integral by converting to polar coordinates. Evaluate the resulting iterated integral. 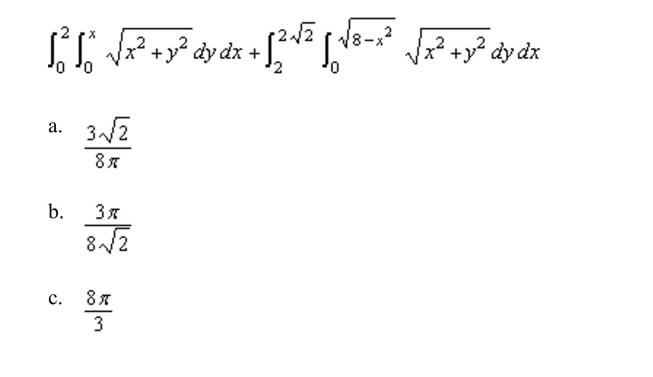
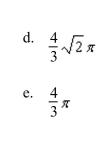
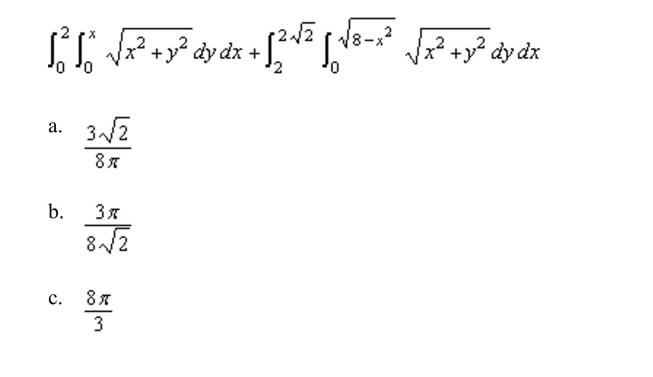
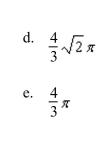

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
26
a double integral in polar coordinates to find the volume of the solid inside the hemisphere 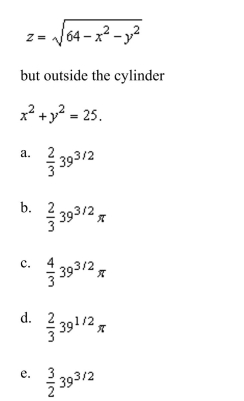
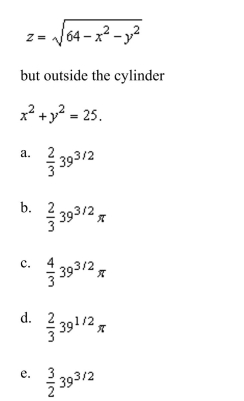

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
27
polar coordinates to describe the region as shown in the figure below: 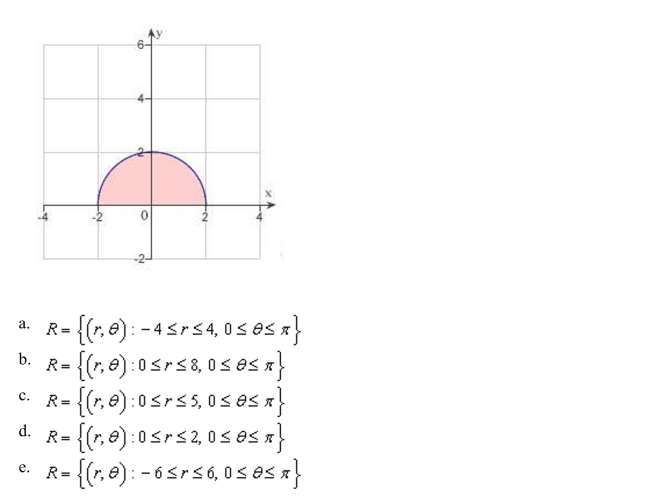


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
28



Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
29
up and evaluate a double integral to find the volume of the solid bounded by the 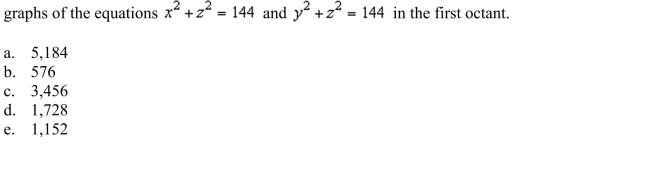
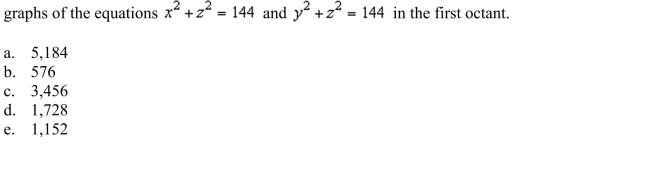

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
30
a double integral to find the volume of the indicated solid. 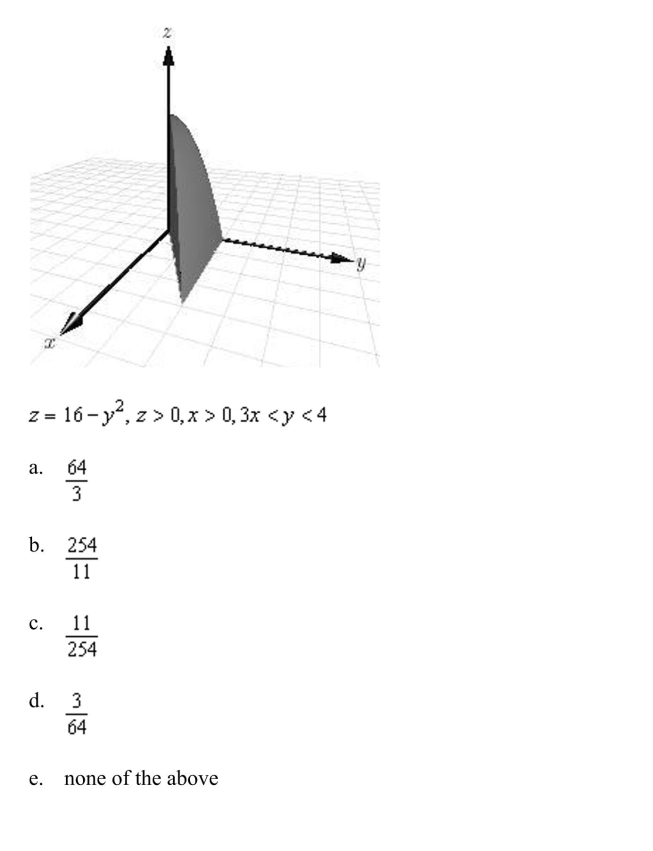


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
31
a double integral in polar coordinates to find the volume of the solid in the first octant bounded by the graphs of the equations given below. 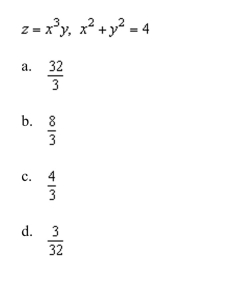
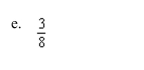
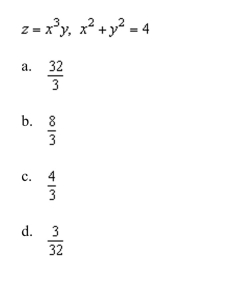
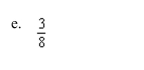

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
32
up and evaluate a double integral to find the volume of the solid bounded by the graphs of the equations given below. 


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
33
Evaluate the double integral below. 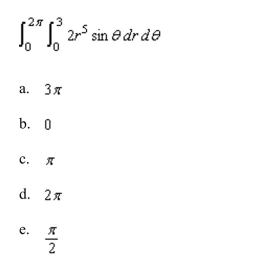
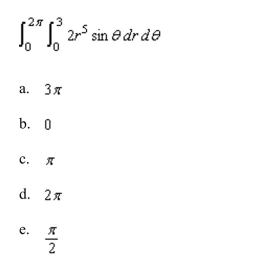

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
34
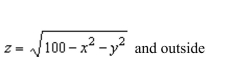 Find a such that the volume inside the hemisphere
Find a such that the volume inside the hemisphere 

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
35
a double integral to find the volume of the indicated solid. 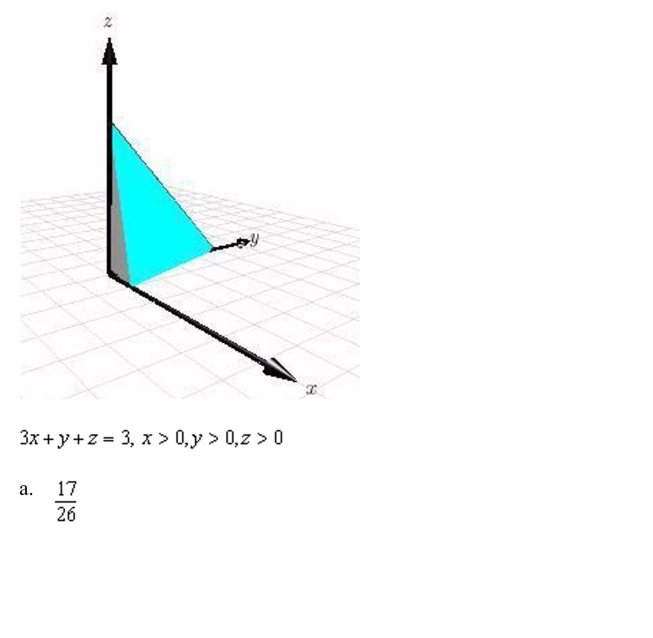
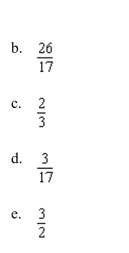

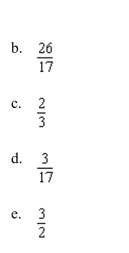

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
36
Evaluate the double integral below. 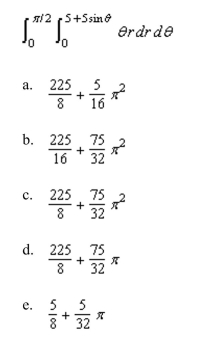
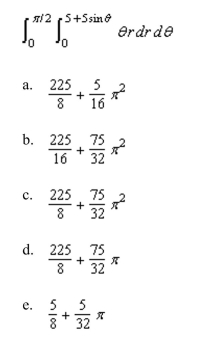

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
37
up and evaluate a double integral to find the volume of the solid bounded by the graphs of the equations given below. 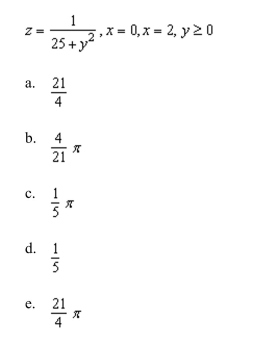
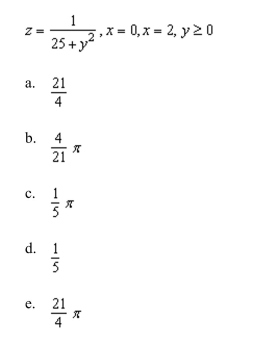

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
38
up an integral for both orders of integration, and use the more convenient order to evaluate the integral below over the region R. 


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
39
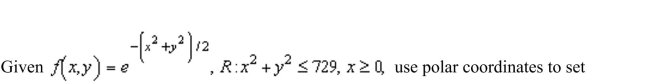
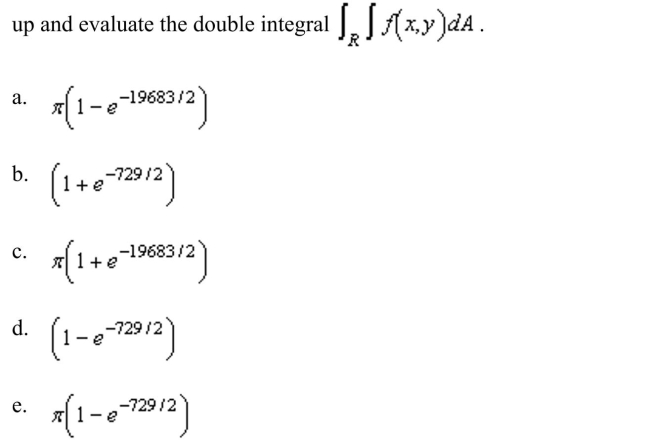

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
40
a double integral to find the volume of the indicated solid. 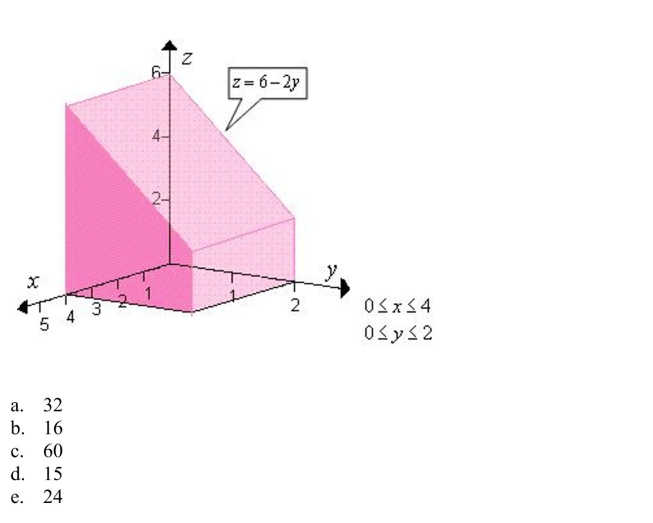


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
41
the center of mass of the rectangular lamina with vertices 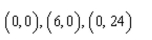
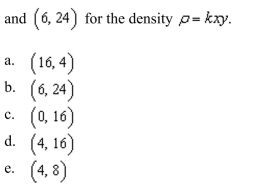
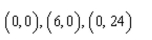
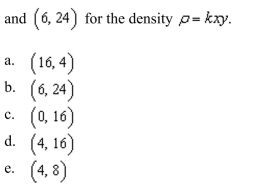

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
42
Determine the diameter of a hole that is drilled vertically through the center of the 


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
43
a double integral to find the area of the shaded region as shown in the figure below. 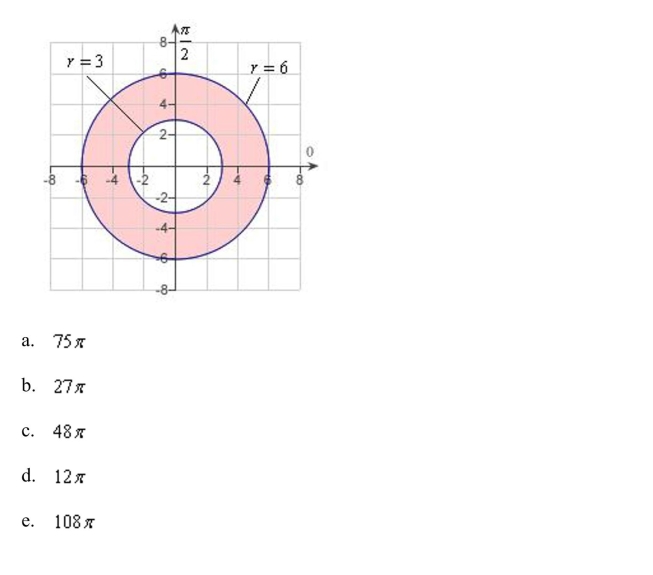


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
44
the mass of the lamina described by the inequalities 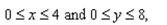

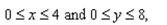


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
45
the mass of the lamina described by the inequalities 


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
46
up the double integral required to find the moment of inertia I, about the line 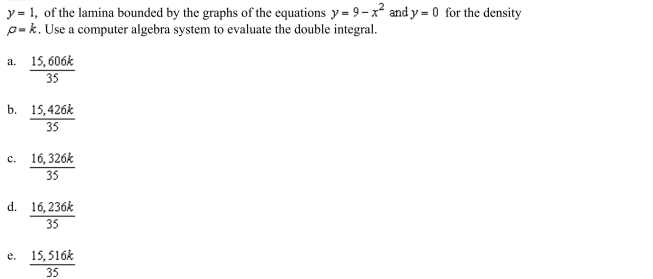
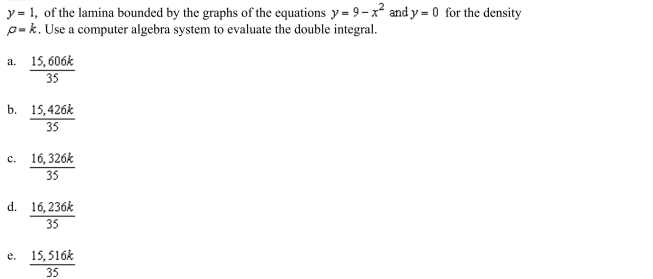

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
47
a double integral to find the area enclosed by the graph of 
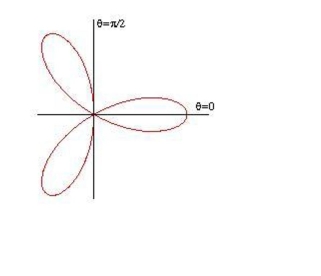
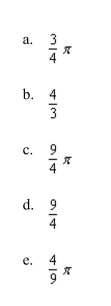


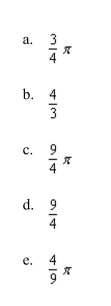

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
48
the center of mass of the lamina bounded by the graphs of the equations 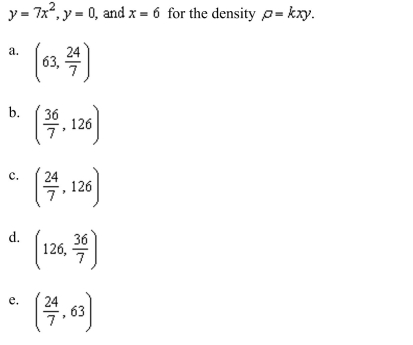
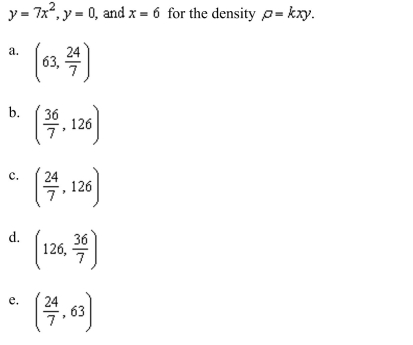

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
49
the mass of the triangular lamina with vertices the density 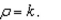
A)401k
B)809k
C)800k
D)400k
E)805k
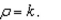
A)401k
B)809k
C)800k
D)400k
E)805k

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
50
the mass of the lamina bounded by the graphs of the equations 

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
51
the center of mass of the lamina bounded by the graphs of the equations 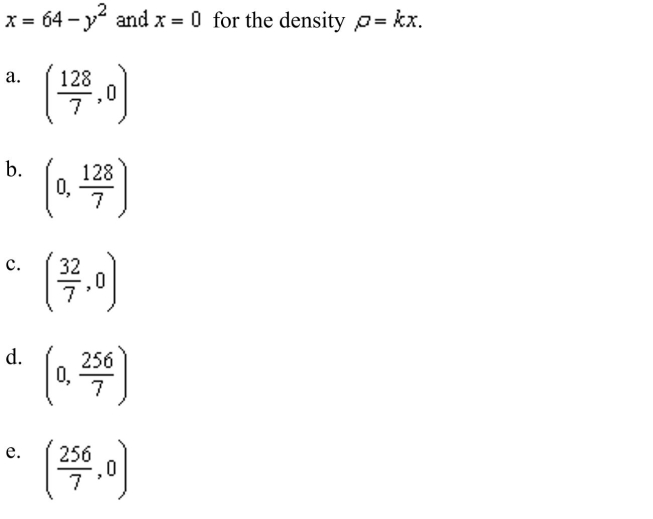
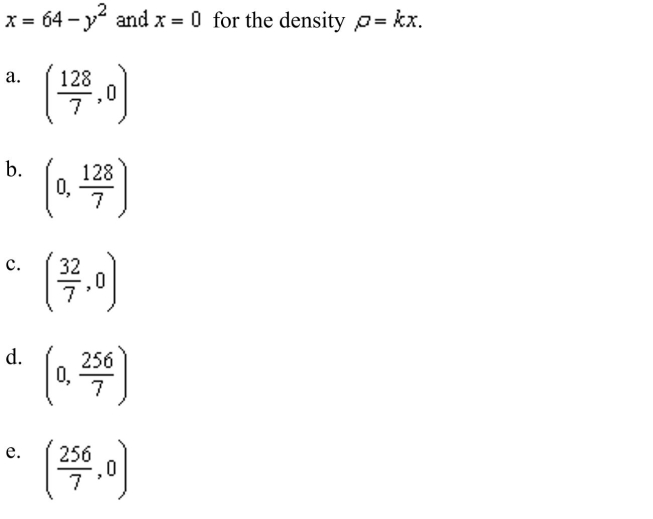

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
52
a double integral to find the area enclosed by the graph of 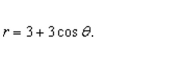
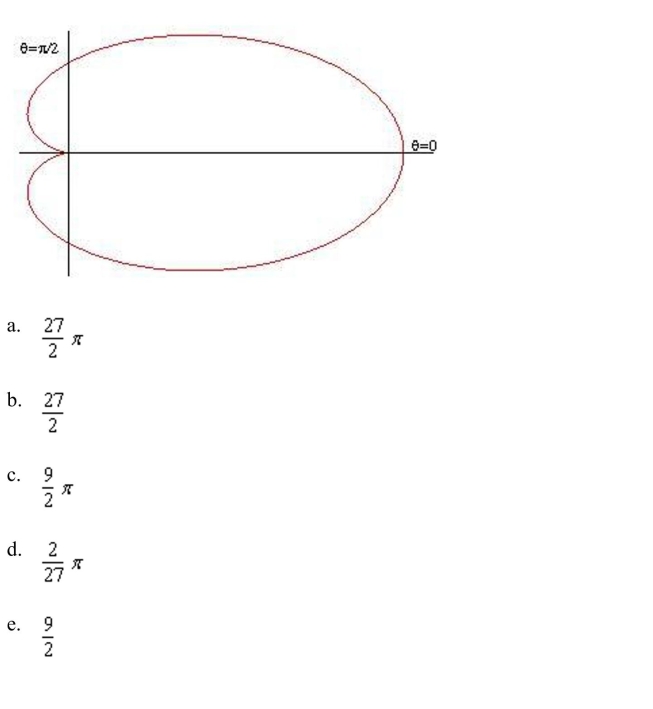
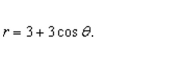


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
53
the mass of the triangular lamina with vertices the density 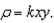

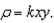


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
54
the mass of the lamina bounded by the graphs of the equations 
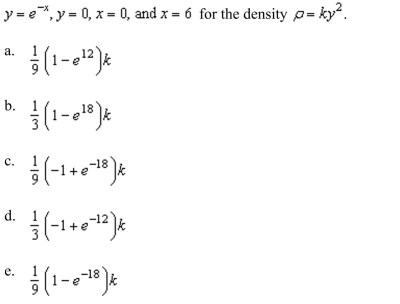

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
55
up and evaluate a double integral required to find the moment of inertia, I, about the given line, of the lamina bounded by the graphs of the following equations. Use a computer
Algebra system to evaluate the double integral.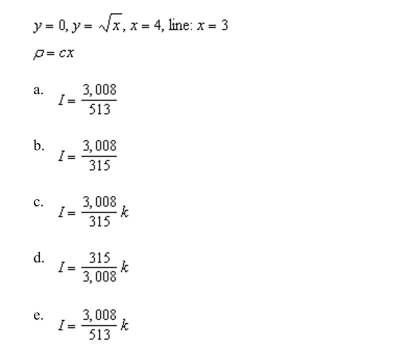
Algebra system to evaluate the double integral.
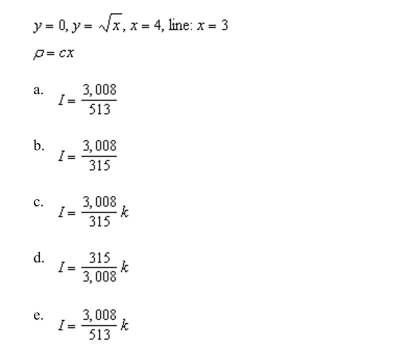

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
56
Suppose the population density of a city is approximated by the model 


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
57
the center of mass of the rectangular lamina with vertices 
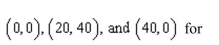

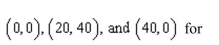

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
58
the mass and center of mass of the lamina bounded by the graphs of the equations given below for the given density. 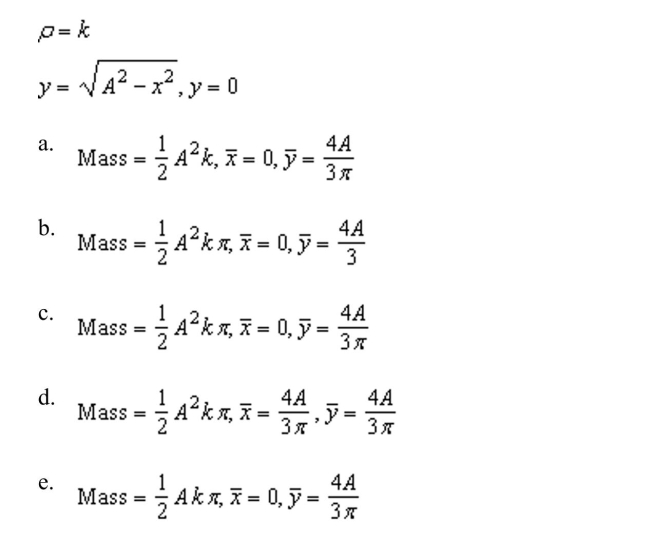
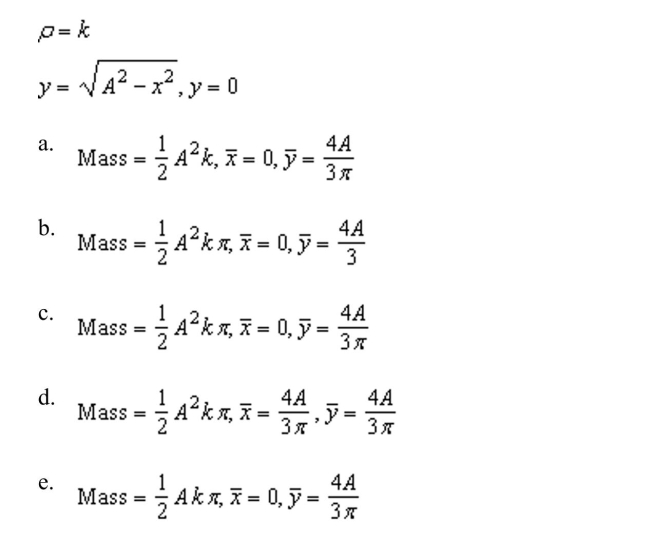

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
59
the center of mass of the lamina bounded by the graphs of the equations 
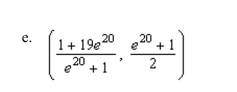

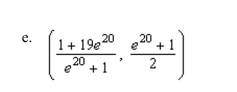

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
60
a double integral to find the area of the region inside the circle 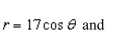 outside the cardioid
outside the cardioid 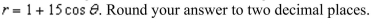
A)46.68
B)58.34
C)20.34
D)55.34
E)22.34
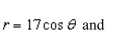 outside the cardioid
outside the cardioid 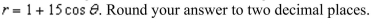
A)46.68
B)58.34
C)20.34
D)55.34
E)22.34

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
61
Evaluate the following iterated integral. 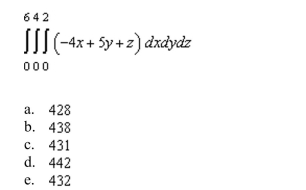
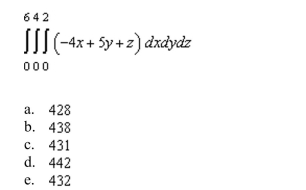

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
62
the area of the portion of the surface 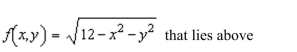 the region
the region 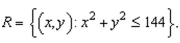 Round your answer to two decimal places.
Round your answer to two decimal places.
A)144.00
B)118.44
C)904.78
D)452.39
E)1,421.22
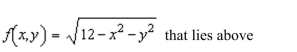 the region
the region 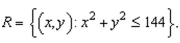 Round your answer to two decimal places.
Round your answer to two decimal places.A)144.00
B)118.44
C)904.78
D)452.39
E)1,421.22

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
63
company produces a spherical object of radius 17 centimeters. A hole of radius 7 centimeters is drilled through the center of the object. Find the volume of the object. 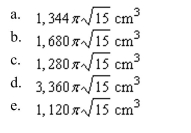
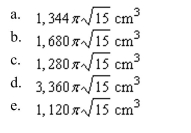

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
64
the area of the surface given by 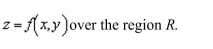
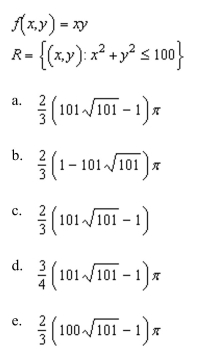
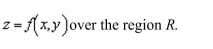
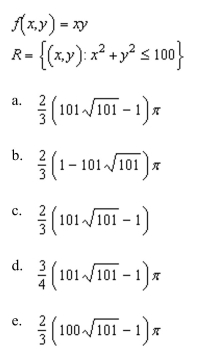

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
65
Write a double integral that represents the surface area of 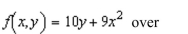 the region R: triangle with vertices
the region R: triangle with vertices 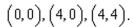 . Use a computer algebra system to evaluate the double integral. Round your answer to two decimal places.
. Use a computer algebra system to evaluate the double integral. Round your answer to two decimal places. 
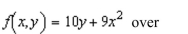 the region R: triangle with vertices
the region R: triangle with vertices 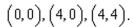 . Use a computer algebra system to evaluate the double integral. Round your answer to two decimal places.
. Use a computer algebra system to evaluate the double integral. Round your answer to two decimal places. 

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
66
the area of the surface for the portion of the paraboloid first
Octant.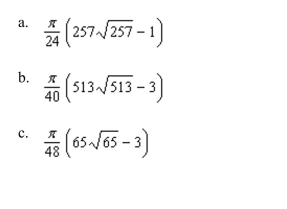
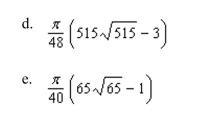
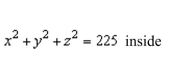
Octant.
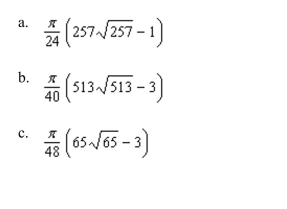
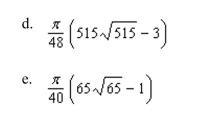
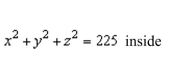

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
67
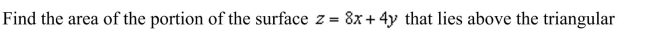


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
68
the area of the portion of the surface 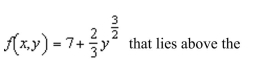

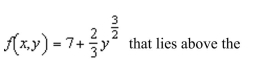


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
69
company produces a spherical object of radius 24 centimeters. A hole of radius 5 centimeters is drilled through the center of the object. Find the outer surface area of the object. 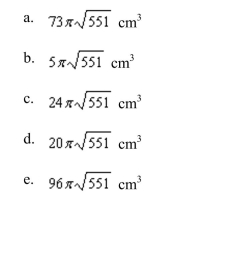
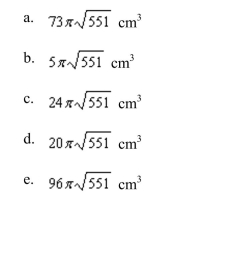

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
70
the area of the surface for the portion of the sphere 


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
71
up a double integral that gives the area of the surface on the graph of 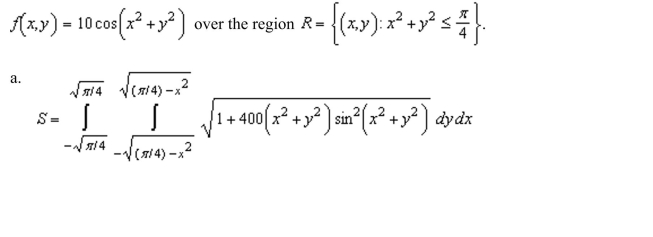
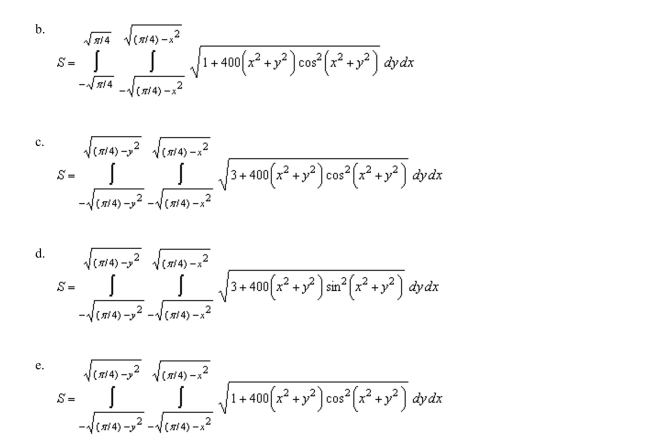
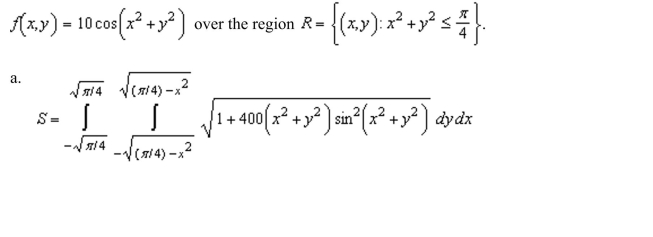


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
72
Determine the location of the horizontal axis 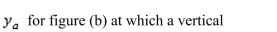 gate in a dam is to be hinged so that there is no moment causing rotation under the indicated loading
gate in a dam is to be hinged so that there is no moment causing rotation under the indicated loading 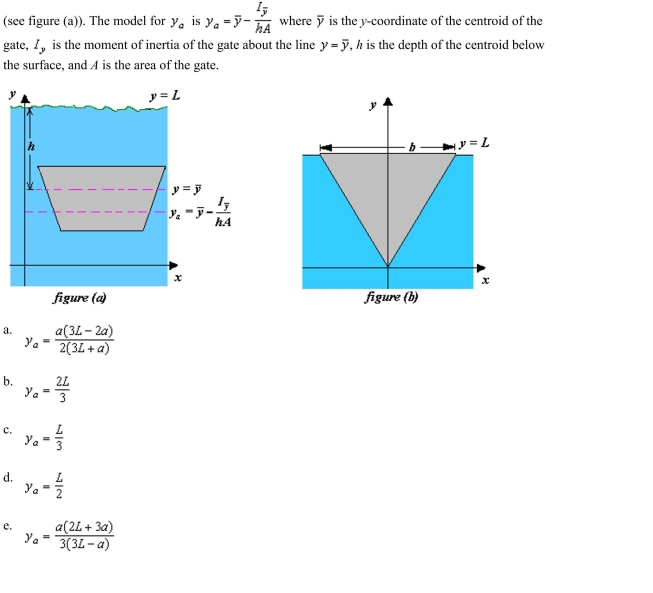
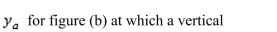 gate in a dam is to be hinged so that there is no moment causing rotation under the indicated loading
gate in a dam is to be hinged so that there is no moment causing rotation under the indicated loading 

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
73
the area of the surface given by 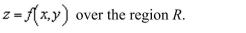

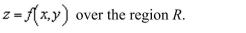


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
74
the area of the surface given by 


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
75
the area of the surface of the portion of the plane 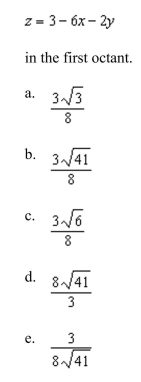
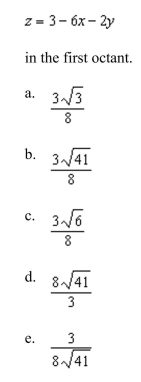

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
76
up a double integral that gives the area of the surface of the graph of f over the region R. 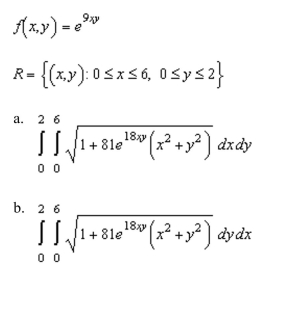
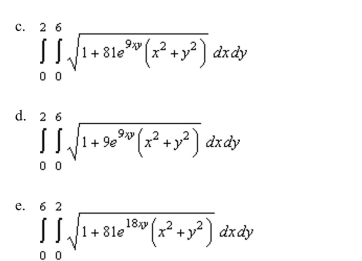
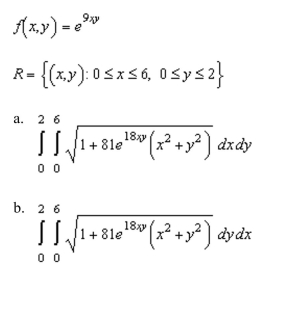
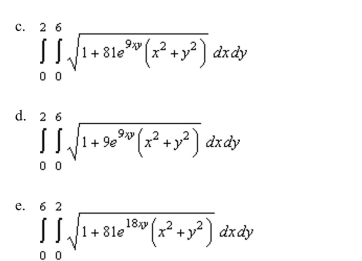

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
77
the area of the portion of the surface 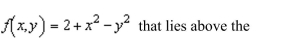

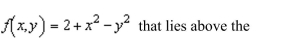


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
78
up a double integral that gives the area of the surface of the graph of f over the region R. 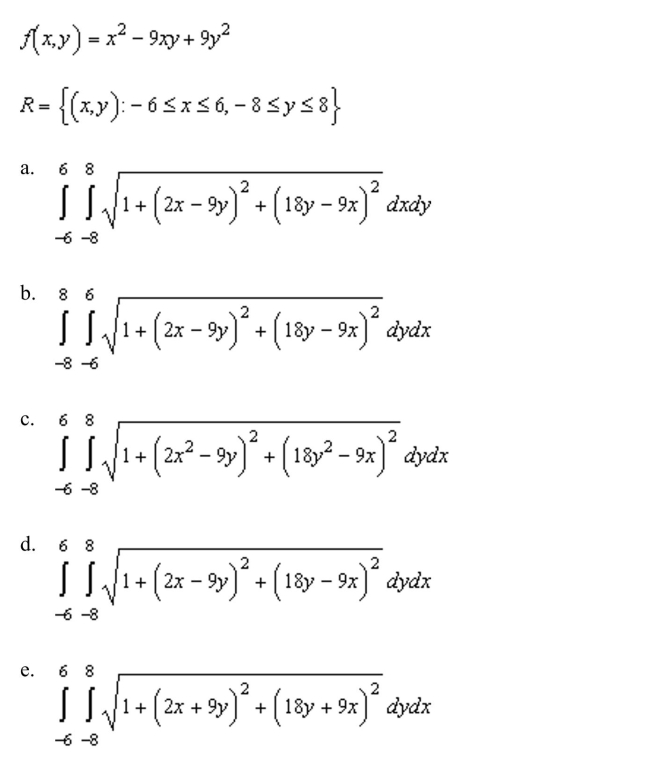
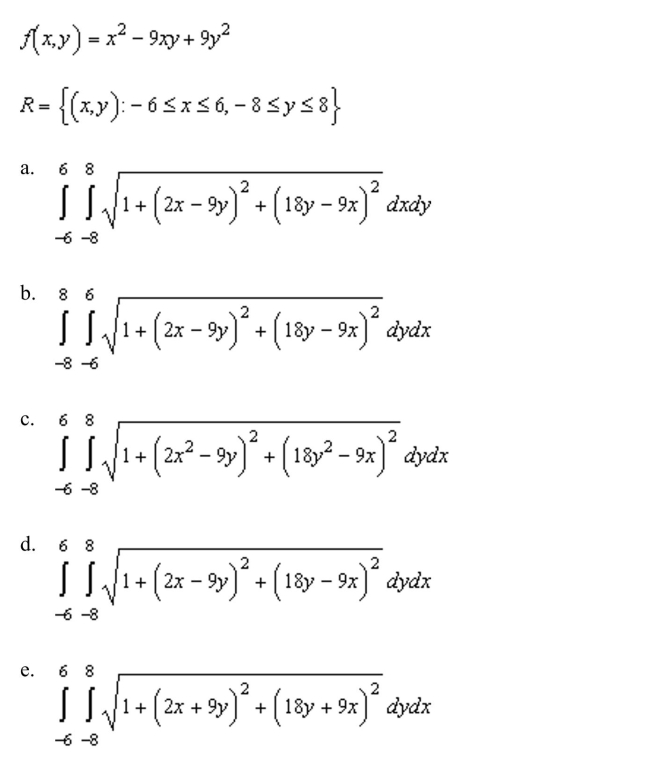

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
79
Determine the location of the horizontal axis 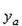 for figure (b) at which a vertical
for figure (b) at which a vertical 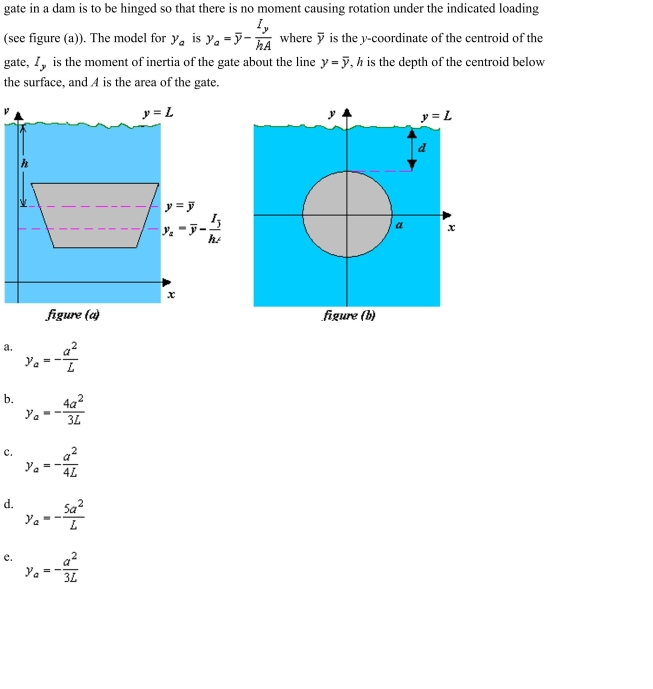
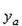 for figure (b) at which a vertical
for figure (b) at which a vertical 

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
80
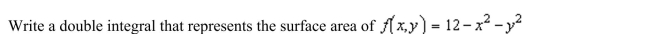


Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck


