Exam 14: Iterated Integrals and Area in the Plane
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Convert the integral below from rectangular coordinates to both cylindrical and spherical coordinates, and evaluate the simpler iterated integral.
Free
(Multiple Choice)
4.8/5  (28)
(28)
Correct Answer:
E
Set up a triple integral for the volume of the solid bounded by the coordinate planes and the plane given below.
Free
(Multiple Choice)
4.9/5  (31)
(31)
Correct Answer:
A
Evaluate the following iterated integral. r dr d
Free
(Multiple Choice)
4.8/5  (33)
(33)
Correct Answer:
A
Use cylindrical coordinates to find the volume of the solid bounded above by and below by .
(Multiple Choice)
4.9/5  (40)
(40)
Find the mass of the triangular lamina with vertices the density
(Multiple Choice)
4.9/5  (30)
(30)
Find the average value of
cube in the first octant bounded by the coordinate planes, and the planes , and . The average value of a continuous function over a solid region is where is the volume of the solid region .
(Multiple Choice)
4.8/5  (43)
(43)
Use a double integral to find the area of the region inside the circle outside the cardioid
(Multiple Choice)
4.8/5  (29)
(29)
tetrahedron in the first octant with vertices and . The average value of a continuous function over a solid region is , where is the volume of the solid region .
(Multiple Choice)
4.8/5  (30)
(30)
order of integration and show that both orders yield the same area. What is this area?
(Multiple Choice)
4.7/5  (42)
(42)
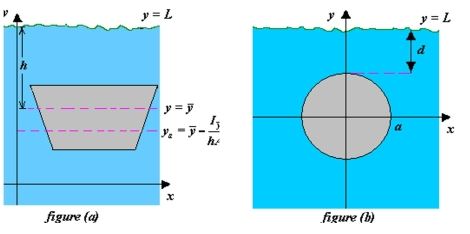
Determine the location of the horizontal axis for figure (b) at which a vertical gate in a dam is to be hinged so that there is no moment causing rotation under the indicated loading (see figure (a)). The model for is where is the -coordinate of the centroid of the gate, is the moment of inertia of the gate about the line is the depth of the centroid below the surface, and is the area of the gate.
(Multiple Choice)
4.8/5  (34)
(34)
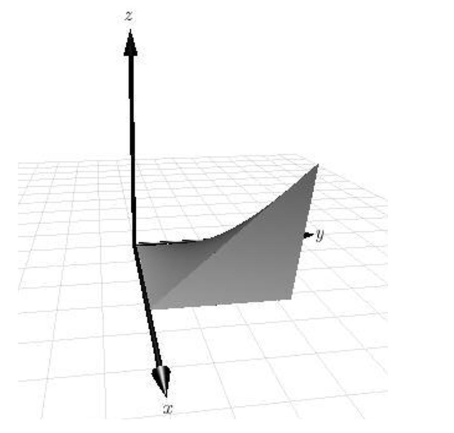
Use a triple integral to find the volume of the solid shown below.
(Multiple Choice)
4.8/5  (29)
(29)
Use a double integral to find the area enclosed by the graph of 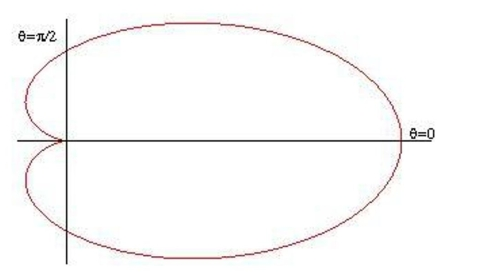
(Multiple Choice)
4.8/5  (32)
(32)
Find the area of the portion of the surface region . Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (33)
(33)
Write a double integral that represents the surface area of the region R: triangle with vertices . Use a computer algebra system to evaluate the double integral. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (34)
(34)
Use a change of variables to find the volume of the solid region lying below the surface and above the plane region : region bounded by the parallelogram with vertices . Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (34)
(34)
Convert the integral below from rectangular coordinates to both cylindrical and spherical coordinates, and evaluate the simpler iterated integral.
(Multiple Choice)
4.9/5  (38)
(38)
Showing 1 - 20 of 118
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)