Deck 15: Vector Fields
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/108
Play
Full screen (f)
Deck 15: Vector Fields
1
a piecewise smooth parametrization of the path C given in the following graph. 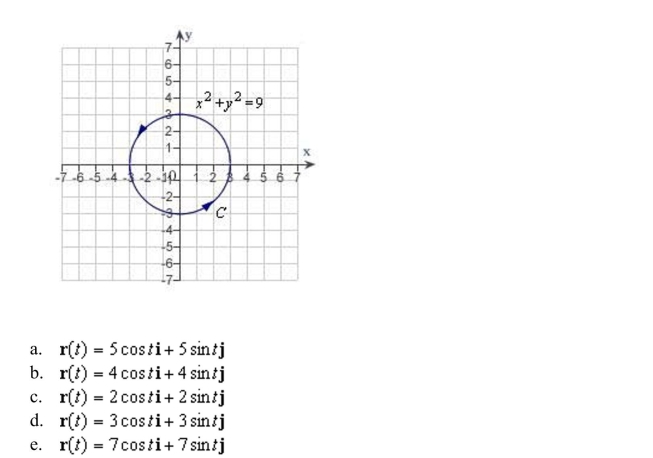

D
2
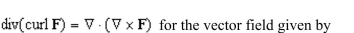
C
3
Sketch the vector field 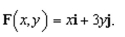
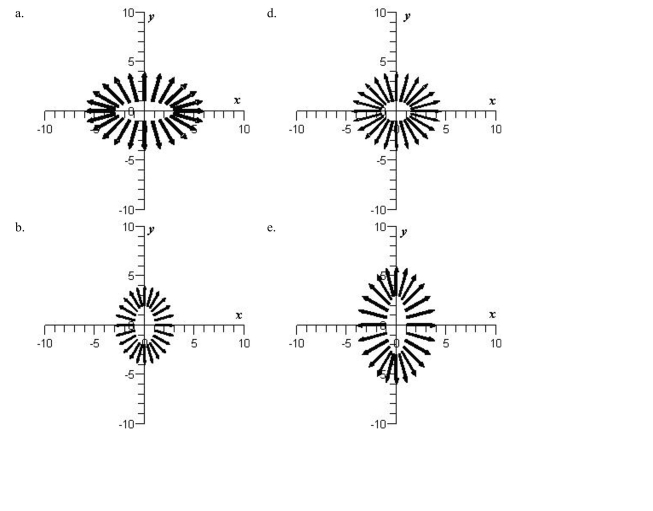
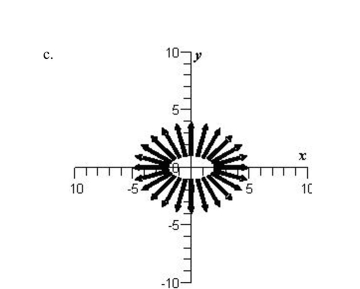
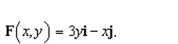
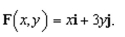


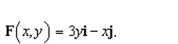
A
4
the conservative vector field for the potential function 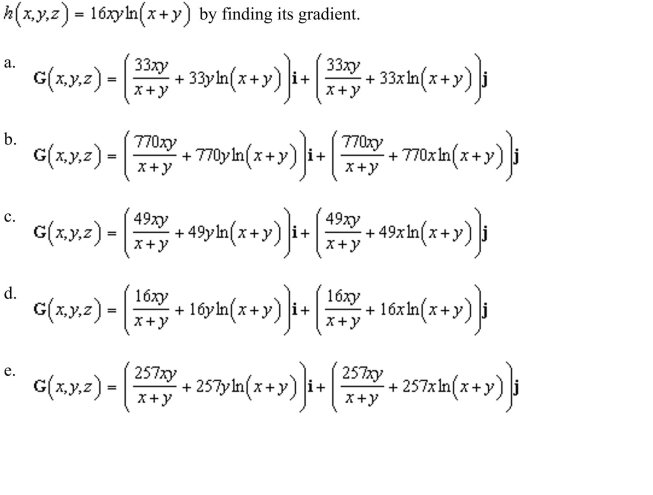
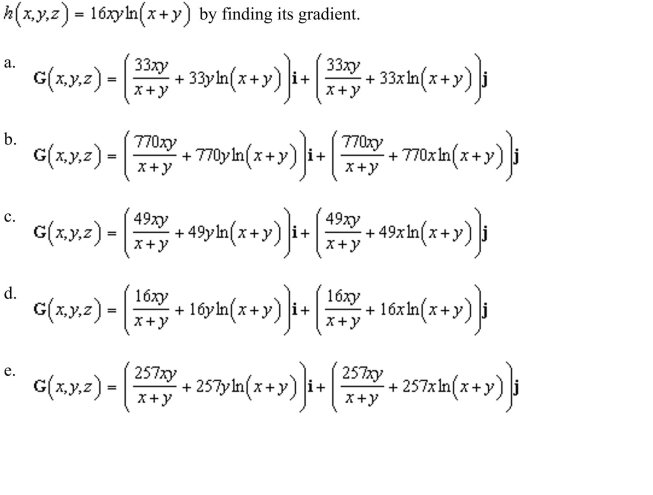

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
5
the work done by the force field 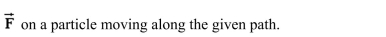
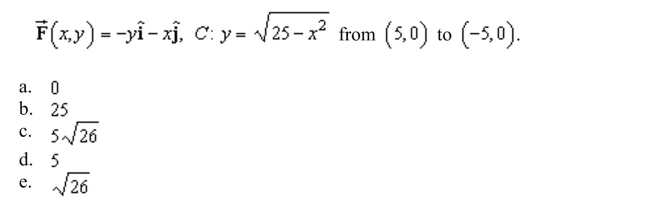
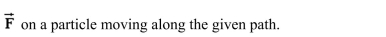
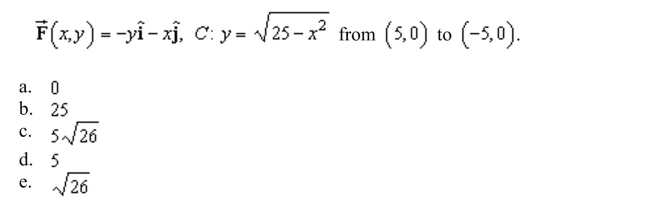

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
6
Determine whether the vector field is conservative. If it is, find a potential function 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
7
the divergence at 

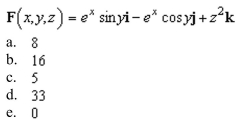

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
8
a piecewise smooth parametrization of the path C given in the following graph. 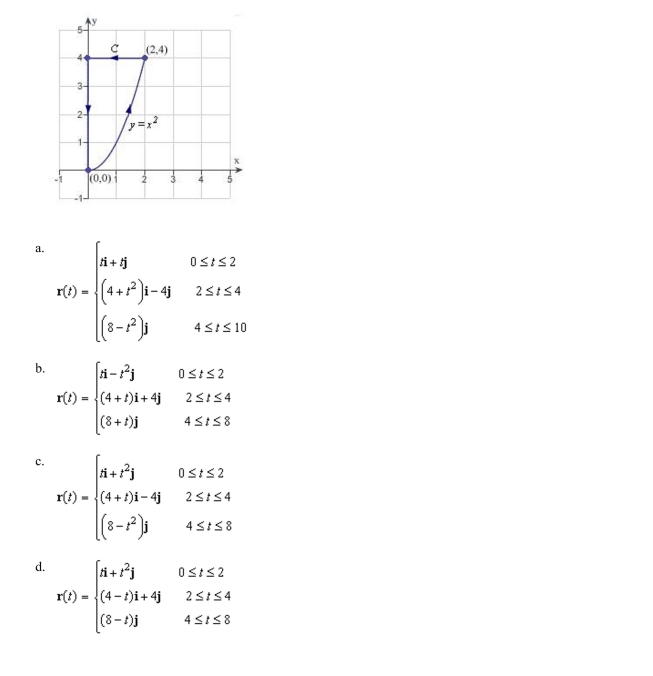
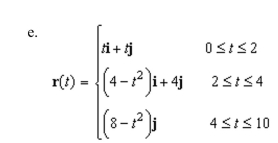

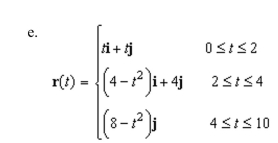

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
9
Determine whether the vector field is conservative. If it is, find a potential function 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate the integral 




Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
11
Determine whether the vector field is conservative. If it is, find a potential function for the vector field. 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
12
the gradient vector for the scalar function. (That is, find the conservative vector field for the potential function.) 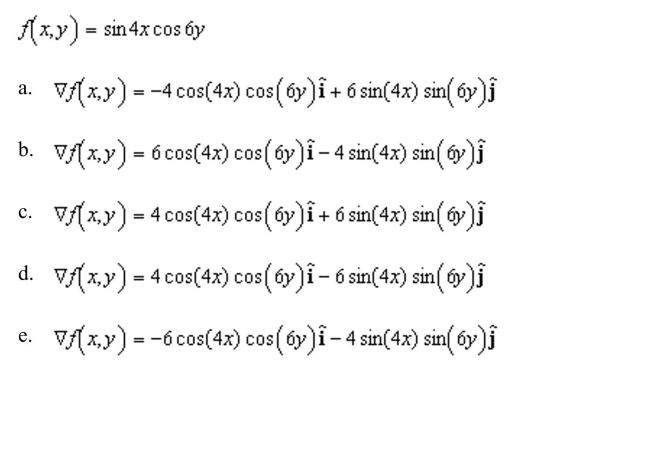
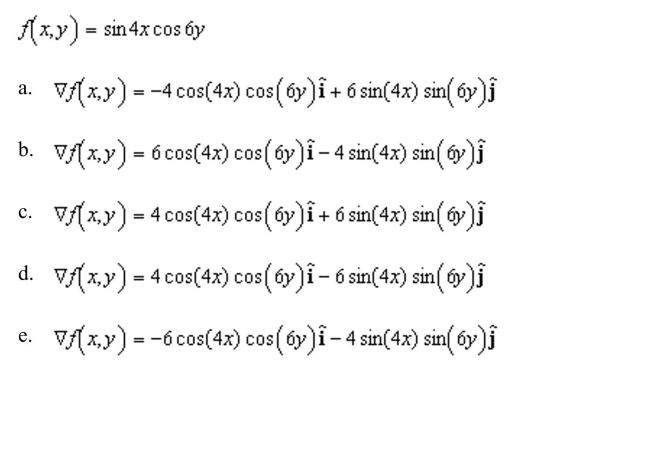

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
13
the divergence of the vector field F given by 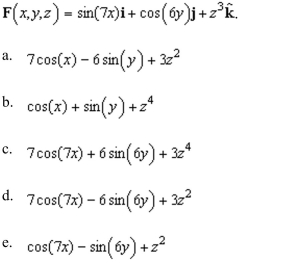
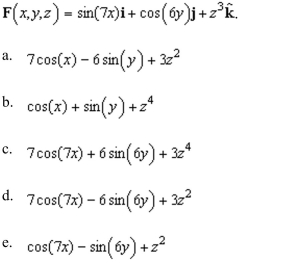

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
14
Evaluate 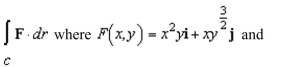

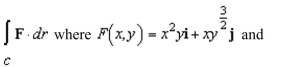


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
15
Evaluate the line integral along the given path. 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
16
the divergence of the vector field. 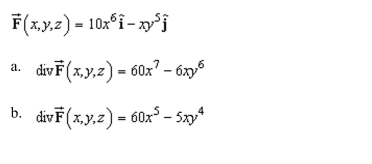
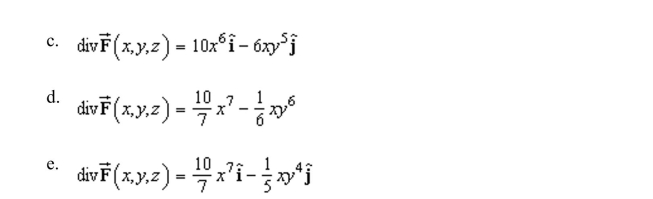
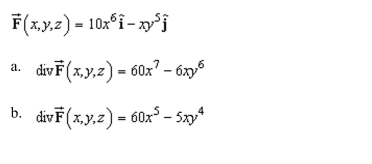
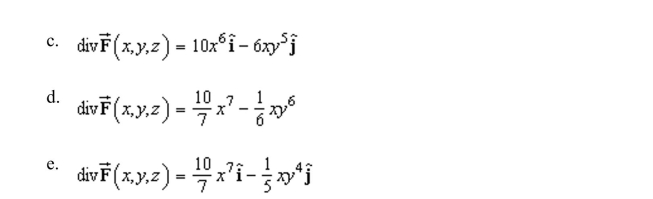

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
17
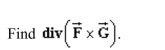
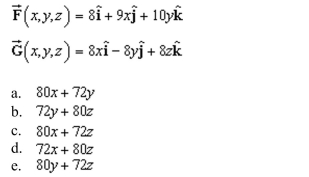

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
18
the curl for the vector field at the given point. 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
19
the gradient vector for the scalar function. (That is, find the conservative vector field for the potential function.) 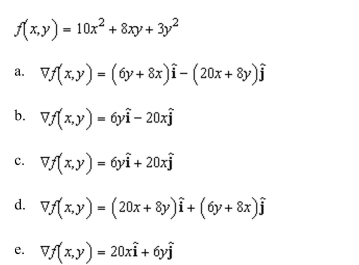
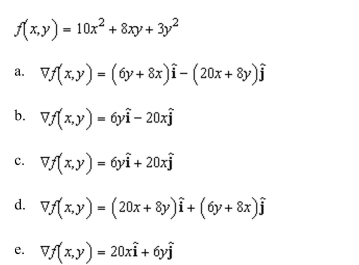

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
20
the divergence of the vector field at the given point. 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
21
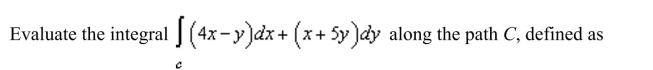
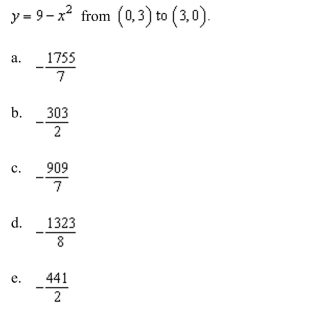

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
22
the vector field  field is conservative.
field is conservative. 
 field is conservative.
field is conservative. 

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
23
the work done by the force field 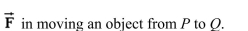
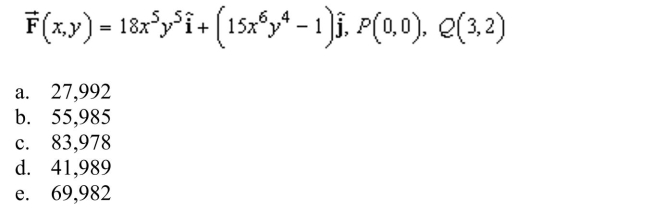
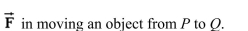
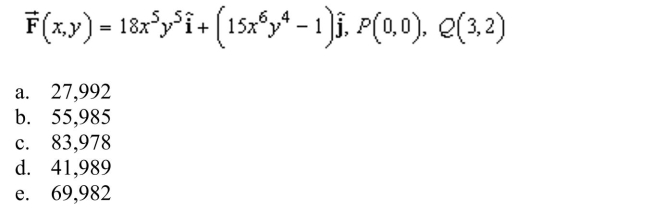

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
24
Calculate the line integral along 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
25
the value of the line integral 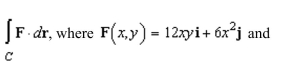

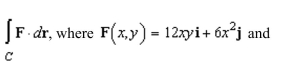


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
26
Evaluate the line integral using the Fundamental Theorem of Line Integrals. Use a computer algebra system to verify your results. 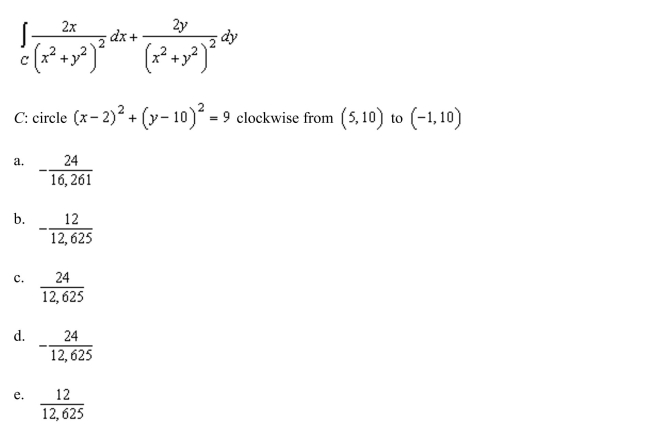
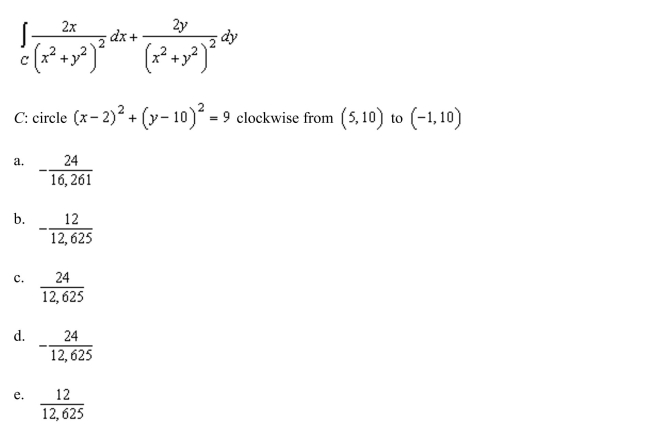

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
27
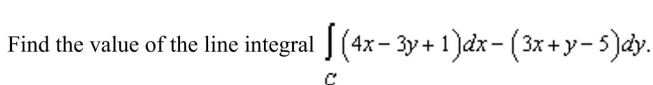 .
. 
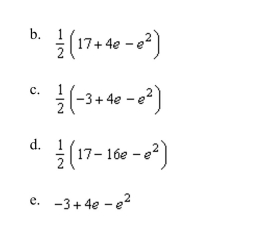

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
28
Calculate the line integral along 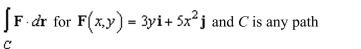

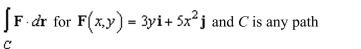


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
29
tractor engine has a steel component with a circular base modeled by the 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
30
the area of the lateral surface over the curve C in the xy-plane and under the 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
31
Evaluate the line integral 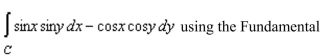



Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
32
the value of the line integral 




Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
33
stone weighing 2 pounds is attached to the end of a four-foot string and is whirled horizontally with one end held fixed. It makes 1 revolution per second. Find the work done by the
Force F that keeps the stone moving in a circular path. [Hint: Use Force = (mass)(centripetal
Acceleration).] Round your answer to two decimal places, if required.![stone weighing 2 pounds is attached to the end of a four-foot string and is whirled horizontally with one end held fixed. It makes 1 revolution per second. Find the work done by the Force F that keeps the stone moving in a circular path. [Hint: Use Force = (mass)(centripetal Acceleration).] Round your answer to two decimal places, if required.](https://storage.examlex.com/TB8682/11eb8bd6_fc45_8a8f_8494_25096a11afd0_TB8682_00.jpg)
Force F that keeps the stone moving in a circular path. [Hint: Use Force = (mass)(centripetal
Acceleration).] Round your answer to two decimal places, if required.
![stone weighing 2 pounds is attached to the end of a four-foot string and is whirled horizontally with one end held fixed. It makes 1 revolution per second. Find the work done by the Force F that keeps the stone moving in a circular path. [Hint: Use Force = (mass)(centripetal Acceleration).] Round your answer to two decimal places, if required.](https://storage.examlex.com/TB8682/11eb8bd6_fc45_8a8f_8494_25096a11afd0_TB8682_00.jpg)

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
34
the work done by a person weighing pounds walking exactly one revolution up a circular helical staircase of radius feet if the person rises feet. 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
35
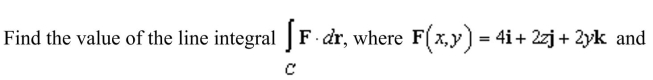


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
36
Determine whether or not the vector field is conservative. 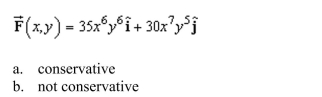
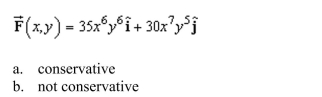

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
37



Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
38
the moments of inertia for a wire that lies along 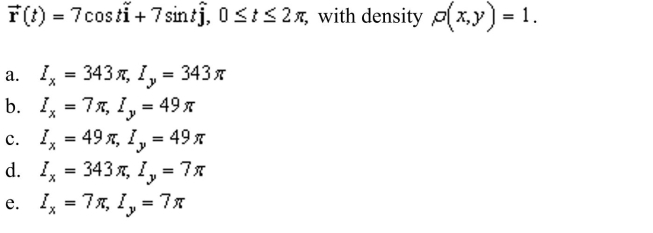
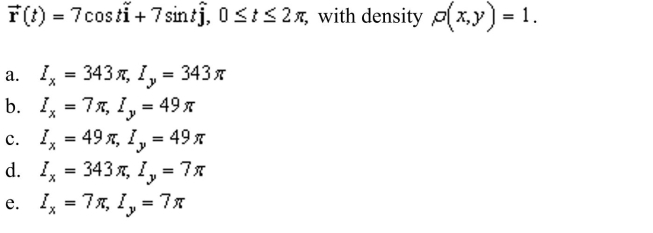

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
39
Evaluate the line integral using the Fundamental Theorem of Line Integrals. Use a computer algebra system to verify your results. 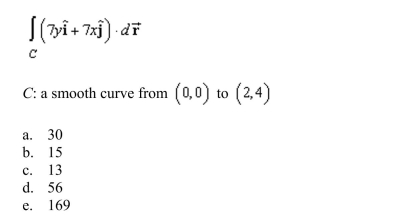
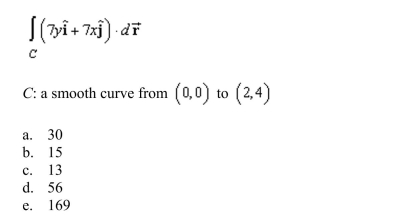

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
40
the value of the line integral 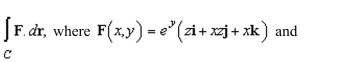

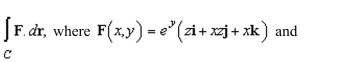


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
41
Green's Theorem to calculate the work done by the force 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
42
Verify Green's Theorem by evaluating both integrals 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
43
up and evaluate a line integral to find the area of the region R bounded by the 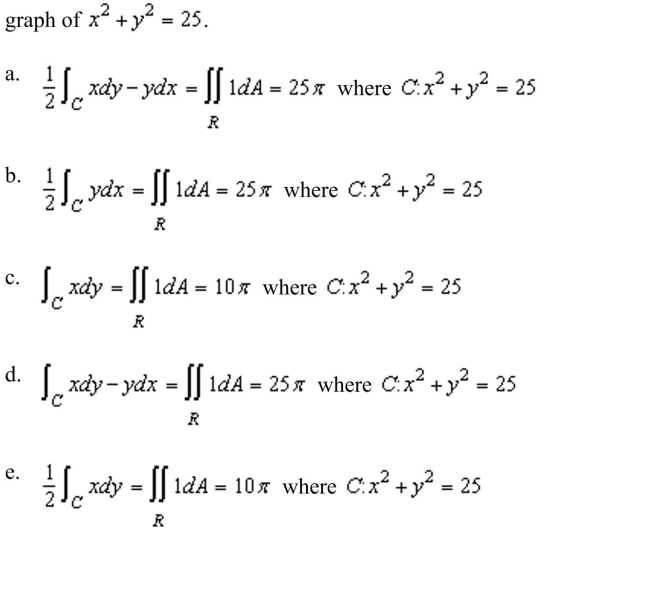
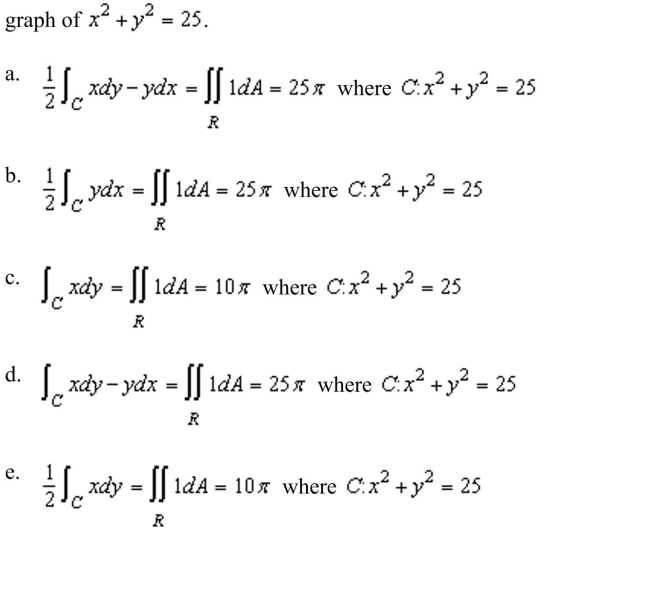

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
44
Identify the surface by eliminating the parameters from the vector-valued function 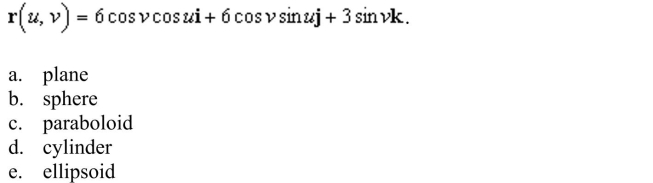
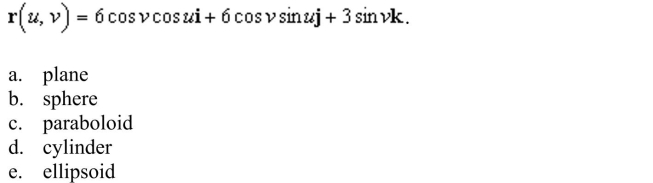

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
45


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
46
Green's Theorem to calculate the work done by the force 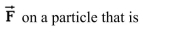 moving counterclockwise around the closed path C.
moving counterclockwise around the closed path C. 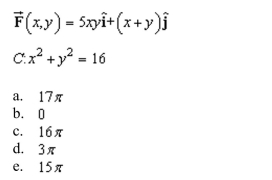
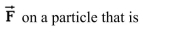 moving counterclockwise around the closed path C.
moving counterclockwise around the closed path C. 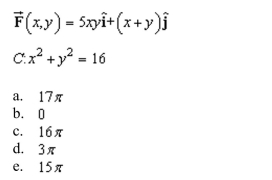

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
47
a computer algebra system and the result "The area of a plane region bounded by the simple closed path C given in polar coordinates is 
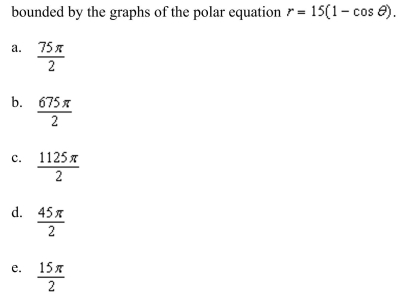

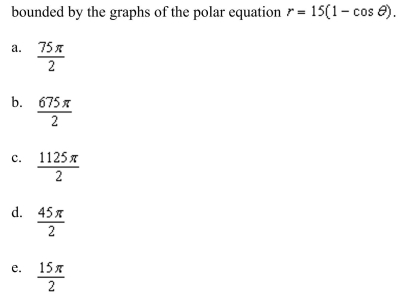

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
48
Green's Theorem to evaluate the integral 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
49
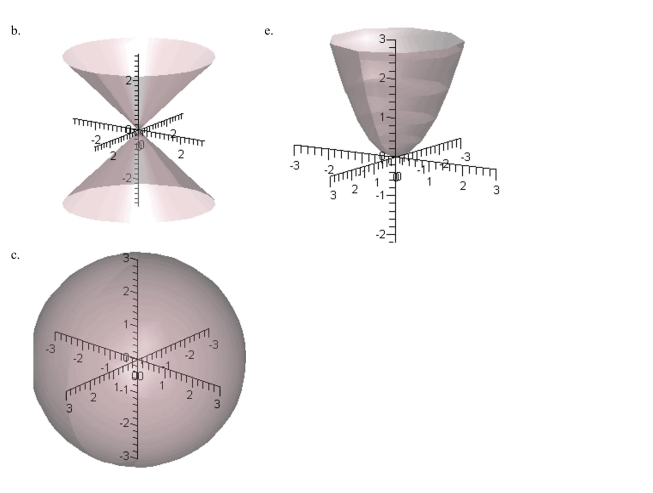
Match the following vector-valued function with its graph. 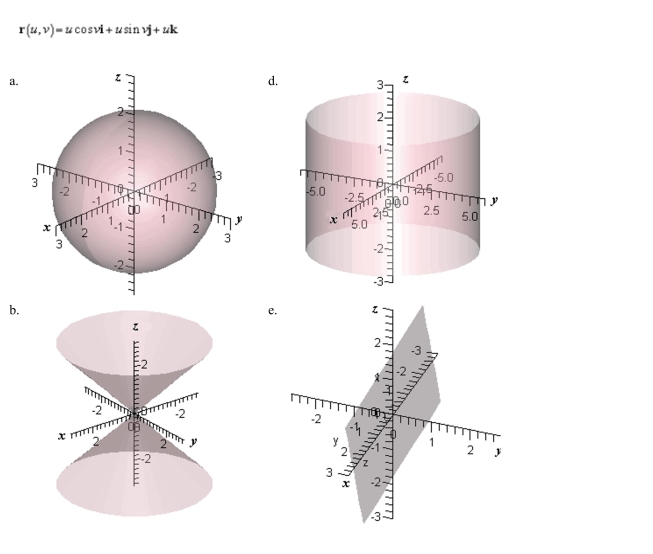
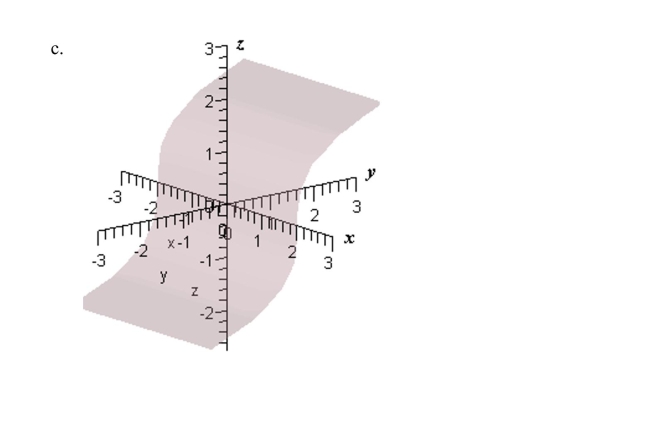



Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
50
Green's Theorem to evaluate the integral 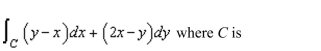
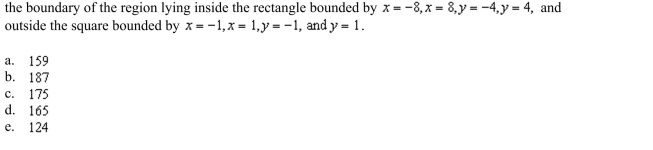
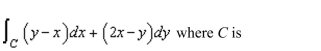
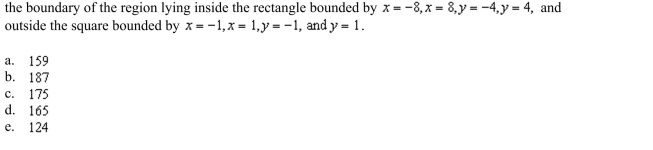

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
51
Green's Theorem to evaluate the line integral 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
52
15. Use a computer algebra system and the result "The area of a plane region bounded by 
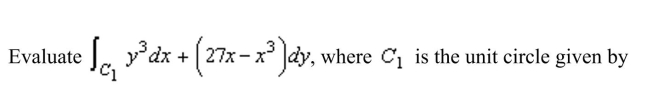

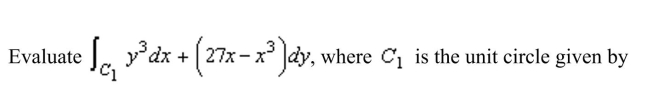

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
53
the rectangular equation for the surface by eliminating parameters from the vector-valued function. Identify the surface. 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
54
the rectangular equation for the surface by eliminating the parameters from the 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
55
Match the following vector -valued function with its graph. 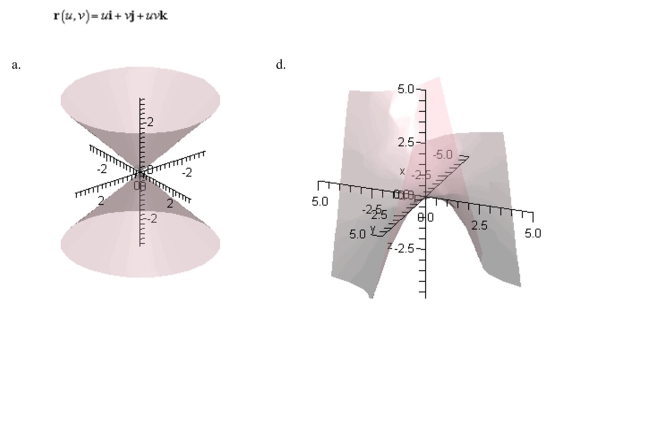
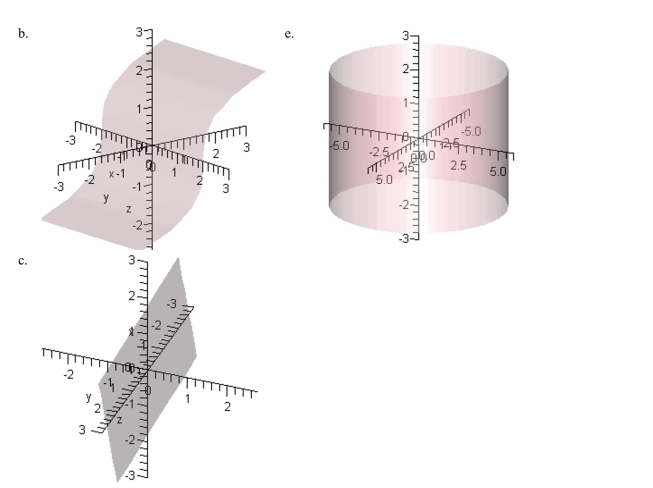



Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
56
Green's Theorem to evaluate the integral 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
57
the maximum value of  in the xy-plane, oriented counterclockwise.
in the xy-plane, oriented counterclockwise. 
 in the xy-plane, oriented counterclockwise.
in the xy-plane, oriented counterclockwise. 

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
58
Green's Theorem to evaluate the line integral 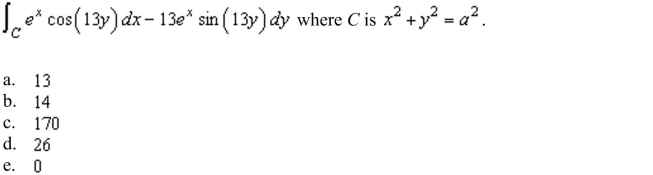
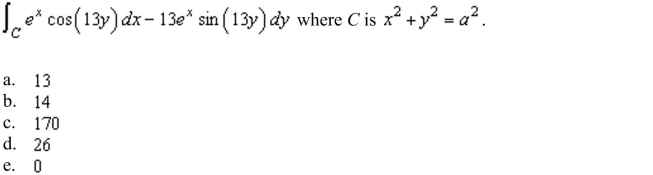

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
59
Green's Theorem to evaluate the integral 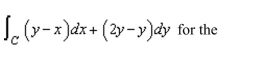
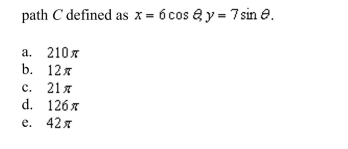
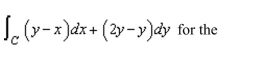
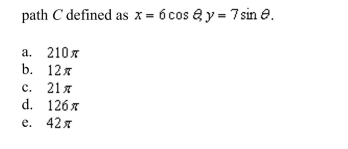

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
60
a computer algebra system and the result "The centroid of the region 
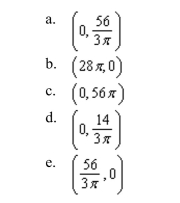

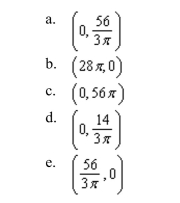

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
61
a computer algebra system to evaluate 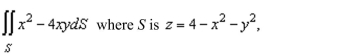

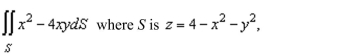


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
62
Write a set of parametric equations for the surface of revolution obtained by revolving the graph of the function about the given axis. 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
63
a vector-valued function for the hyperboloid 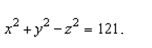
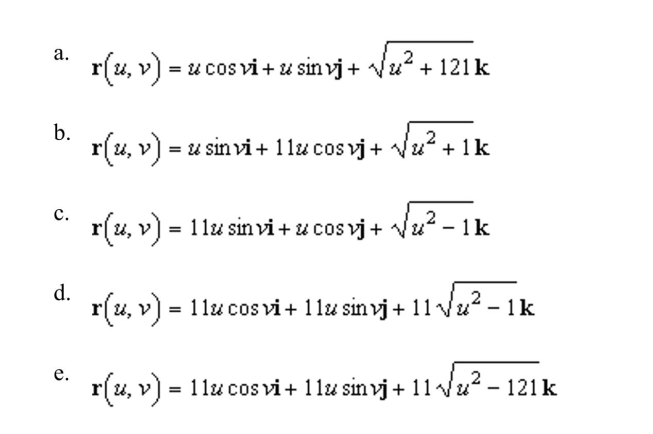
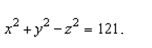
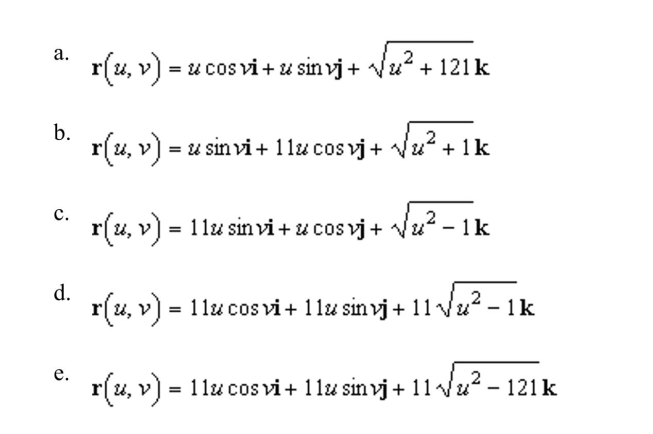

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
64
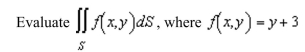
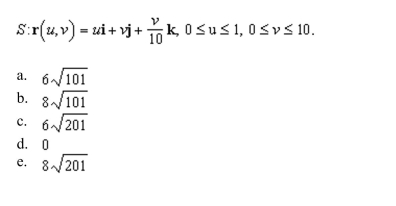

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
65
Write a set of parametric equations for the surface of revolution obtained by 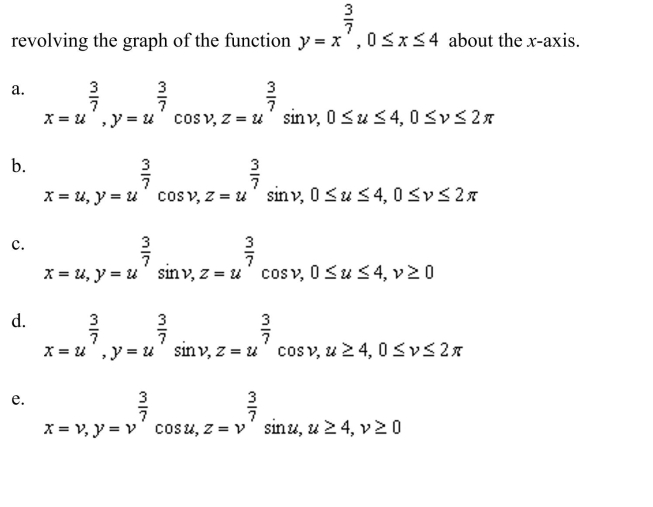
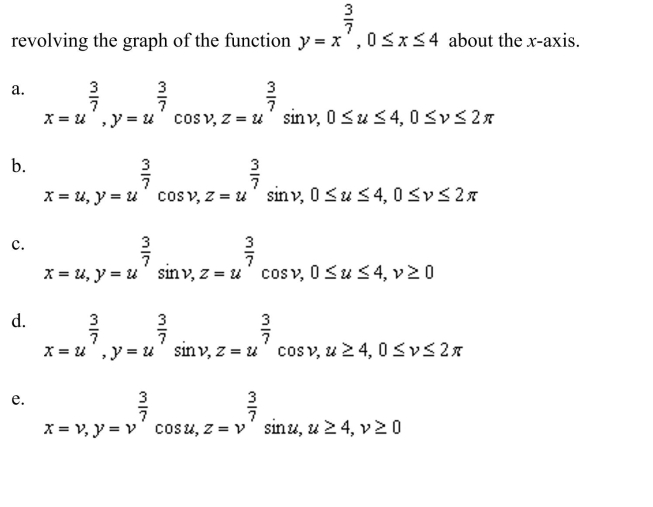

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
66
an equation of the tangent plane to the surface represented by the vector-valued function at the given point. 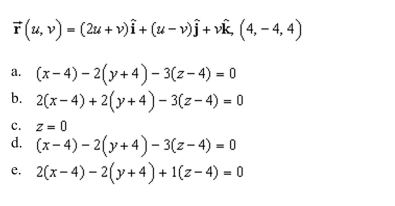
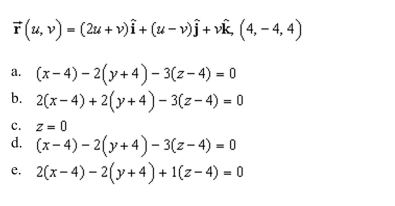

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
67
surface of the dome on a new museum is given by 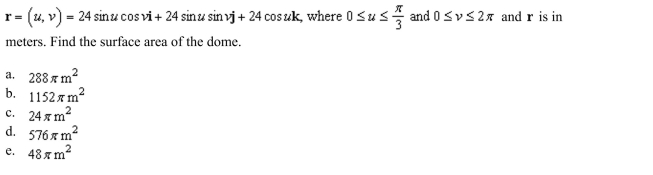
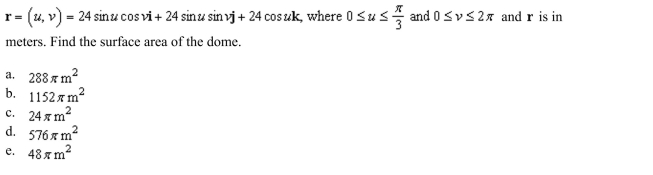

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
68
a vector-valued function whose graph is the plane 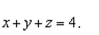
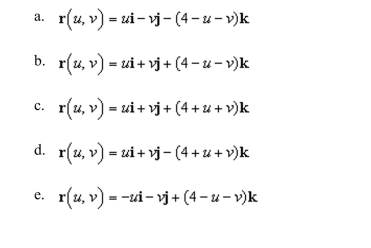
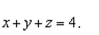
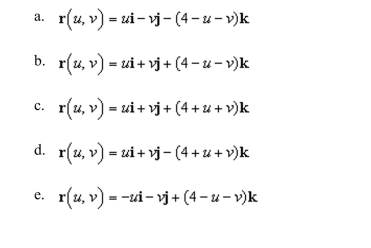

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
69
a computer algebra system to evaluate 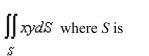

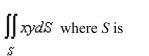


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
70
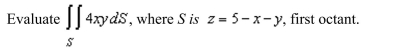
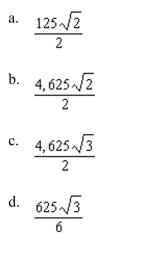

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
71
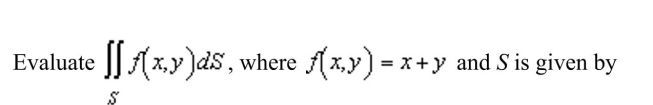
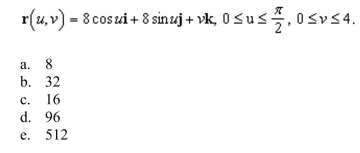

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
72
Determine the tangent plane for the hyperboloid 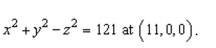
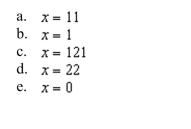
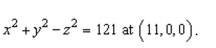
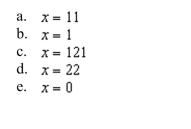

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
73
the rectangular equation for the surface by eliminating the parameters from the 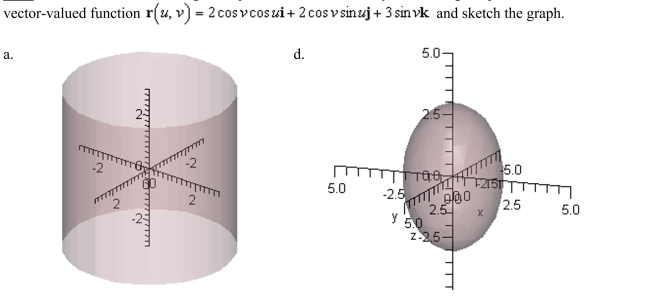



Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
74
the area of the surface of revolution 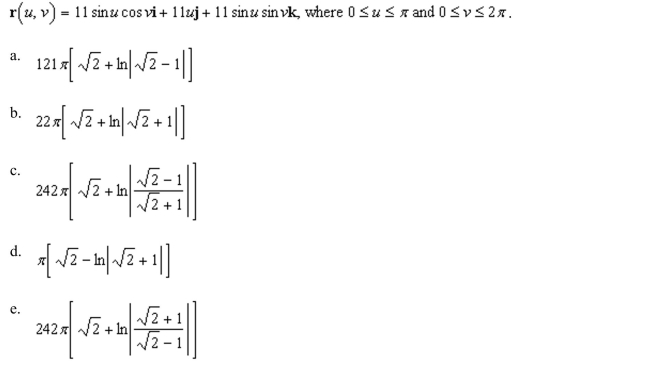
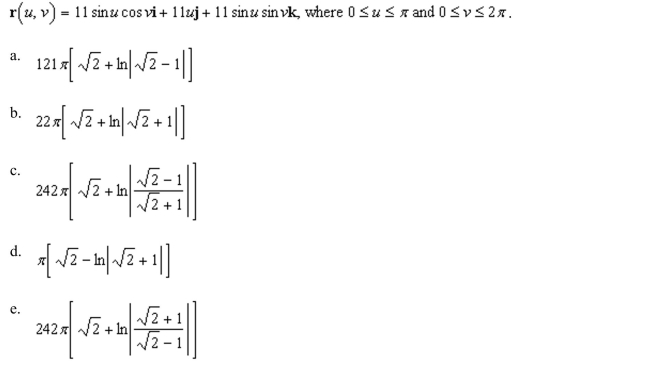

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
75
the area of the surface over the given region. Use a computer algebra system to verify your results.
The part of the cone,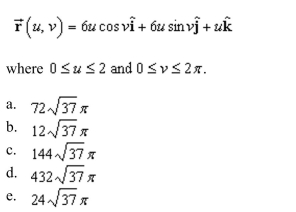
The part of the cone,
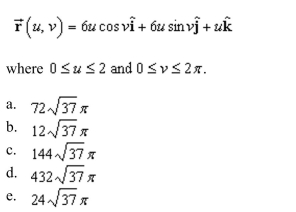

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
76



Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
77
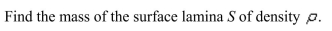
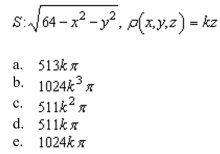

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
78
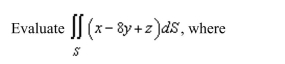
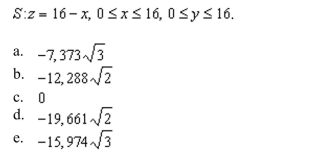

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
79
the area of the surface over the given region. Use a computer algebra system to verify your results. 


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
80
the area of the surface given by 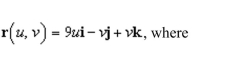
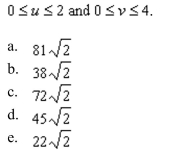
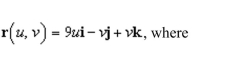
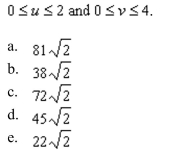

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck


