Deck 9: Vectors in Two and Three Dimensions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/150
Play
Full screen (f)
Deck 9: Vectors in Two and Three Dimensions
1
Use DeMoivre's Theorem to find the indicated power. 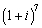
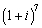
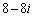
2
Convert the equation to polar form.
3
Convert the polar equation to rectangular coordinates.
4
Graph the polar equation .

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
5
Test the polar equation for symmetry with respect to the polar axis, the pole, and the line .

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
6
Convert the point whose polar coordinates are to rectangular coordinates.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
7
Sketch a graph of the rectangular equation. [Hint: First convert the equation to polar coordinates.] ![Sketch a graph of the rectangular equation. [Hint: First convert the equation to polar coordinates.]](https://storage.examlex.com/TB8630/11eb96c8_1886_e02d_8cd3_67b79ab0d22a_TB8630_11.jpg)
![Sketch a graph of the rectangular equation. [Hint: First convert the equation to polar coordinates.]](https://storage.examlex.com/TB8630/11eb96c8_1886_e02d_8cd3_67b79ab0d22a_TB8630_11.jpg)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
8
Convert the equation to polar form. 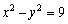
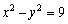

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
9
Convert the rectangular coordinates to polar coordinates with

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
10
Test the polar equation for symmetry with respect to the polar axis, the pole, and the line .

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
11
Write in polar form then find

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
12
Find two polar coordinate representations for the point , one with , and the other with

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
13
Convert the polar equation to rectangular coordinates.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
14
Convert the rectangular coordinates to polar coordinates with

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
15
Write the complex conjugate of z in polar form with argument between 0 and

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
16
Let and . Find

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
17
Write the complex number in polar form. 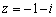
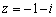

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
18
Sketch a graph of the polar equation.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
19
Let and . Find

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
20
Find the modulus and the argument for the complex number.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
21
Convert the equation to polar form.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
22
Find the cube roots of

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
23
If a projectile is fired with an initial speed of ft/s at an angle
above the horizontal, then its position after t seconds is given by the parametric equations
where x and y are measured in feet.Suppose a gun fires a bullet into the air with an initial speed of 1024 ft/s at an angle of to the horizontal. What is the maximum height attained by the bullet?
above the horizontal, then its position after t seconds is given by the parametric equations
where x and y are measured in feet.Suppose a gun fires a bullet into the air with an initial speed of 1024 ft/s at an angle of to the horizontal. What is the maximum height attained by the bullet?

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
24
Convert the rectangular coordinates to polar coordinates with

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
25
Test the polar equation for symmetry with respect to the polar axis, the pole, and the line .

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
27
Convert the point whose polar coordinates are 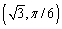
to rectangular coordinates.
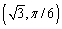
to rectangular coordinates.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
28
Find the modulus and the argument for the complex number.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
29
Graph the polar equation

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
30
Sketch a graph of the rectangular equation. [Hint: First convert the equation to polar coordinates.] ![Sketch a graph of the rectangular equation. [Hint: First convert the equation to polar coordinates.]](https://storage.examlex.com/TB8630/11eb96c8_188b_e97f_8cd3_5f4c0338524f_TB8630_11.jpg)
![Sketch a graph of the rectangular equation. [Hint: First convert the equation to polar coordinates.]](https://storage.examlex.com/TB8630/11eb96c8_188b_e97f_8cd3_5f4c0338524f_TB8630_11.jpg)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
31
Convert the equation to polar form.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
32
Convert the polar equation to rectangular coordinates.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
33
Sketch the curve represented by the parametric equations and find its rectangular-coordinate equation. 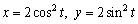
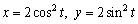

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
34
Convert the polar equation to rectangular coordinates. 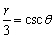
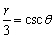

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
35
Sketch a graph of the polar equation.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
36
Find parametric equations for the line with the given properties.Passing through 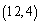
and the origin
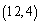
and the origin

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
37
Test the polar equation for symmetry with respect to the polar axis, the pole, and the line .

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
38
Find two polar coordinate representations for the point , one with , and both with

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
39
Find a rectangular-coordinate equation for the curve by eliminating the parameter. 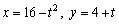
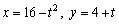

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
40
Convert the rectangular coordinates to polar coordinates with

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
41
Test the polar equation for symmetry with respect to the polar axis, the pole, and the line .
I
II
III
A)I only
B)I and II
C) I and III
D)II and III
E) none of these
I
II
III
A)I only
B)I and II
C) I and III
D)II and III
E) none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
42
Which of the following is not a polar point representation for the point 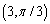 ?
?
A)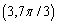
B)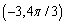
C)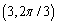
D)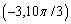
E)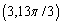
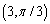 ?
?A)
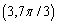
B)
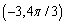
C)
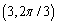
D)
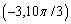
E)
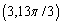

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
43
Sketch the curve represented by the parametric equations and find its rectangular-coordinate equation. 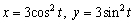
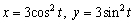

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
44
Write the complex conjugate of z in polar form with argument between 0 and

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
45
Convert the polar equation to rectangular coordinates.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
46
Find a rectangular-coordinate equation for the curve by eliminating the parameter. 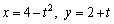
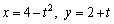

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the equation. 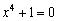
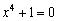

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
48
Write in polar form then find

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
49
Let and . Find

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
50
Convert the equation to polar form.
A)
B)
C)
D)
E)none of these
A)
B)
C)
D)
E)none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
51
Convert the rectangular coordinates to polar coordinates with 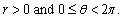
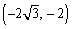
A)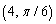
B)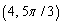
C)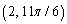
D)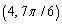
E)none of these
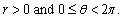
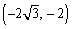
A)
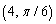
B)
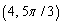
C)
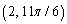
D)
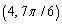
E)none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
53
Convert the polar equation to rectangular coordinates.
A)
B)
C)
D)
E)none of these
A)
B)
C)
D)
E)none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
54
Graph the polar equation
A)
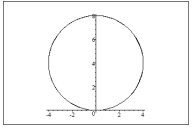
B)
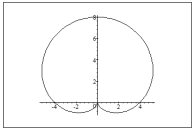
C)
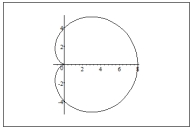
D)
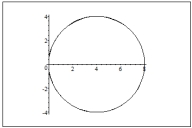
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
56
Convert the point whose polar coordinates are to rectangular coordinates
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
57
Convert the rectangular coordinates to polar coordinates with 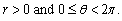
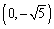
A)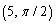
B)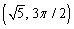
C)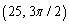
D)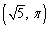
E)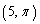
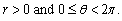
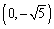
A)
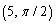
B)
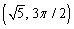
C)
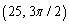
D)
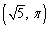
E)
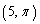

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
58
Convert the equation to polar form.
A)
B)
C)
D)
E)none of these
A)
B)
C)
D)
E)none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
59
Find parametric equations for the line with the given properties.Passing through 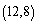
and the origin
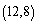
and the origin

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
60
Use DeMoivre's Theorem to find the indicated power.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
61
Let and ) Find
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
62
Which of the following is not a polar point representation for the point 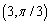 ?
?
A)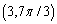
B)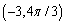
C)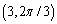
D)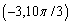
E)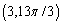
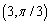 ?
?A)
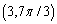
B)
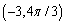
C)
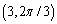
D)
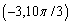
E)
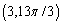

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
63
Write the complex conjugate of z in polar form with argument between 0 and
A)
B)
C)
D)
E) none
A)
B)
C)
D)
E) none

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
64
Sketch a graph of the polar equation.
A)
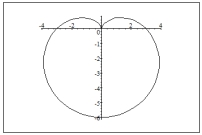
B)
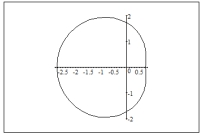
C)
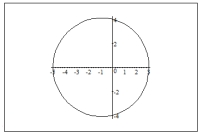
D)
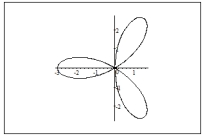
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
65
Find the modulus and the argument for the complex number.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
66
Let and ) Find
A)
B)
C)
D)
E)none
A)
B)
C)
D)
E)none

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
67
Find the rectangular-coordinate equation for the parametric equations given. 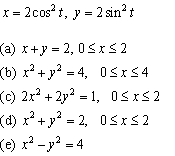
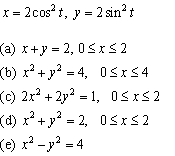

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
68
Convert the point whose polar coordinates are 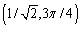 to rectangular coordinates
to rectangular coordinates
A)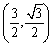
B)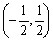
C)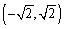
D)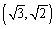
E)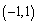
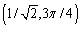 to rectangular coordinates
to rectangular coordinatesA)
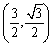
B)
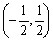
C)
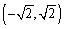
D)
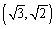
E)
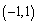

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
69
Write the complex number in polar form.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the equation. 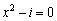
A)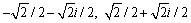
B)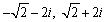
C)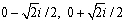
D)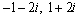
E)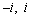
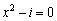
A)
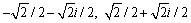
B)
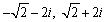
C)
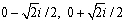
D)
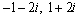
E)
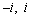

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
71
Test the polar equation for symmetry with respect to the polar axis, the pole, and the line .
I
II
III
A)I only
B)I and II
C) I and III
D)II and III
E) I, II, III
I
II
III
A)I only
B)I and II
C) I and III
D)II and III
E) I, II, III

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
72
Graph the polar equation
A)
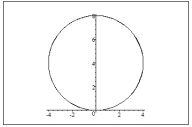
B)
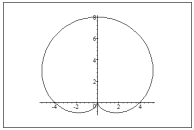
C)
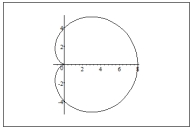
D)
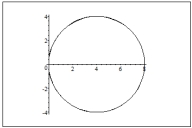
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
73
Use DeMoivre's Theorem to find the indicated power. 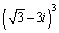
A)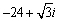
B)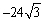
C)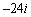
D)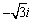
E)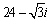
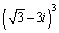
A)
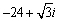
B)
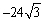
C)
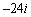
D)
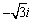
E)
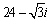

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
74
Find parametric equations for the line with the given properties.Passing through 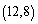 and the origin
and the origin
A)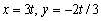
B)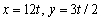
C)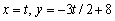
D)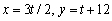
E)none of these
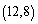 and the origin
and the originA)
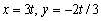
B)
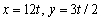
C)
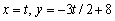
D)
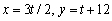
E)none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
75
Write 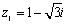 in polar form then find
in polar form then find 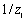
A)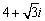
B)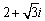
C)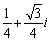
D)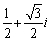
E)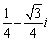
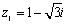 in polar form then find
in polar form then find 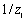
A)
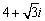
B)
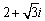
C)
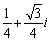
D)
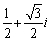
E)
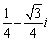

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
76
Sketch a graph of the rectangular equation. [Hint: First convert the equation to polar coordinates.]
A)
![<strong>Sketch a graph of the rectangular equation. [Hint: First convert the equation to polar coordinates.] \left( x ^ { 2 } + y ^ { 2 } + 3 y \right) ^ { 2 } = 9 \left( x ^ { 2 } + y ^ { 2 } \right) </strong> A) B) C) D)](https://storage.examlex.com/TB8630/11eb96c8_1893_14d8_8cd3_032bea2b9a5e_TB8630_11.jpg)
B)
![<strong>Sketch a graph of the rectangular equation. [Hint: First convert the equation to polar coordinates.] \left( x ^ { 2 } + y ^ { 2 } + 3 y \right) ^ { 2 } = 9 \left( x ^ { 2 } + y ^ { 2 } \right) </strong> A) B) C) D)](https://storage.examlex.com/TB8630/11eb96c8_1893_14d9_8cd3_4f7073ac6f69_TB8630_11.jpg)
C)
![<strong>Sketch a graph of the rectangular equation. [Hint: First convert the equation to polar coordinates.] \left( x ^ { 2 } + y ^ { 2 } + 3 y \right) ^ { 2 } = 9 \left( x ^ { 2 } + y ^ { 2 } \right) </strong> A) B) C) D)](https://storage.examlex.com/TB8630/11eb96c8_1893_14da_8cd3_eb946951fb11_TB8630_11.jpg)
D)
![<strong>Sketch a graph of the rectangular equation. [Hint: First convert the equation to polar coordinates.] \left( x ^ { 2 } + y ^ { 2 } + 3 y \right) ^ { 2 } = 9 \left( x ^ { 2 } + y ^ { 2 } \right) </strong> A) B) C) D)](https://storage.examlex.com/TB8630/11eb96c8_1893_14db_8cd3_2d5e209bc976_TB8630_11.jpg)
A)
![<strong>Sketch a graph of the rectangular equation. [Hint: First convert the equation to polar coordinates.] \left( x ^ { 2 } + y ^ { 2 } + 3 y \right) ^ { 2 } = 9 \left( x ^ { 2 } + y ^ { 2 } \right) </strong> A) B) C) D)](https://storage.examlex.com/TB8630/11eb96c8_1893_14d8_8cd3_032bea2b9a5e_TB8630_11.jpg)
B)
![<strong>Sketch a graph of the rectangular equation. [Hint: First convert the equation to polar coordinates.] \left( x ^ { 2 } + y ^ { 2 } + 3 y \right) ^ { 2 } = 9 \left( x ^ { 2 } + y ^ { 2 } \right) </strong> A) B) C) D)](https://storage.examlex.com/TB8630/11eb96c8_1893_14d9_8cd3_4f7073ac6f69_TB8630_11.jpg)
C)
![<strong>Sketch a graph of the rectangular equation. [Hint: First convert the equation to polar coordinates.] \left( x ^ { 2 } + y ^ { 2 } + 3 y \right) ^ { 2 } = 9 \left( x ^ { 2 } + y ^ { 2 } \right) </strong> A) B) C) D)](https://storage.examlex.com/TB8630/11eb96c8_1893_14da_8cd3_eb946951fb11_TB8630_11.jpg)
D)
![<strong>Sketch a graph of the rectangular equation. [Hint: First convert the equation to polar coordinates.] \left( x ^ { 2 } + y ^ { 2 } + 3 y \right) ^ { 2 } = 9 \left( x ^ { 2 } + y ^ { 2 } \right) </strong> A) B) C) D)](https://storage.examlex.com/TB8630/11eb96c8_1893_14db_8cd3_2d5e209bc976_TB8630_11.jpg)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
77
Find a rectangular-coordinate equation for the curve by eliminating the parameter. 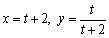
A)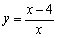
B)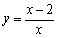
C)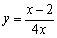
D)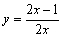
E) none of these
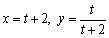
A)
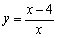
B)
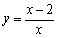
C)
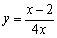
D)
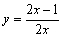
E) none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
79
If a projectile is fired with an initial speed of 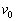 ft/s at an angle
ft/s at an angle 
Above the horizontal, then its position after t seconds is given by the parametric equations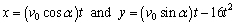
Where x and y are measured in feet. Suppose a gun fires a bullet into the air with an initial speed of 1024 ft/s at an angle of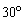
To the horizontal. How far from the gun will the bullet hit the ground?
A)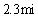
B)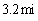
C)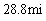
D)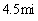
E)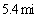
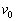 ft/s at an angle
ft/s at an angle 
Above the horizontal, then its position after t seconds is given by the parametric equations
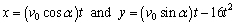
Where x and y are measured in feet. Suppose a gun fires a bullet into the air with an initial speed of 1024 ft/s at an angle of
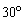
To the horizontal. How far from the gun will the bullet hit the ground?
A)
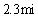
B)
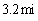
C)
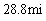
D)
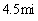
E)
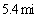

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
80
Convert the rectangular coordinates to polar coordinates with 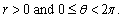
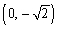
A)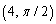
B)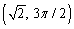
C)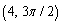
D)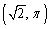
E)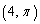
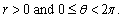
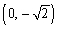
A)
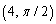
B)
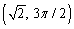
C)
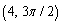
D)
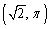
E)
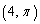

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
81
Sketch a graph of the polar equation.
A)
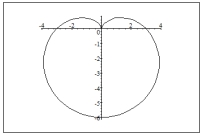
B)
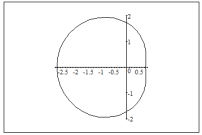
C)
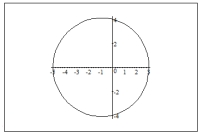
D)
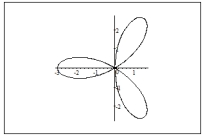
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
82
Let and ) Find
A)
B)
C)
D)
E)none
A)
B)
C)
D)
E)none

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
83
Convert the polar equation to rectangular coordinates. 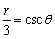
A)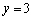
B)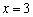
C)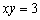
D)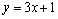
E)none
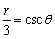
A)
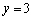
B)
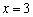
C)
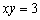
D)
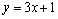
E)none

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
86
Find a rectangular-coordinate equation for the curve by eliminating the parameter.
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck


