Deck 10: Characteristics of Functions and Their Graphs
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/142
Play
Full screen (f)
Deck 10: Characteristics of Functions and Their Graphs
1
Classify the function as continuous or discontinuous.
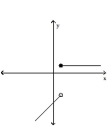
A)continuous
B)discontinuous

A)continuous
B)discontinuous
discontinuous
2
Classify the function as continuous or discontinuous.
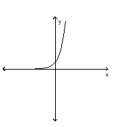
A)discontinuous
B)continuous

A)discontinuous
B)continuous
continuous
3
Classify the function as continuous or discontinuous.
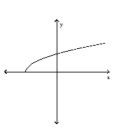
A)discontinuous
B)continuous

A)discontinuous
B)continuous
continuous
4
Graph the piecewise function.
-
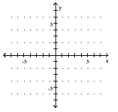
A)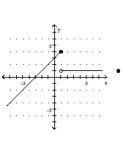
B)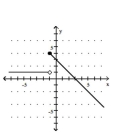
C)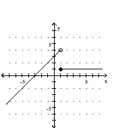
D)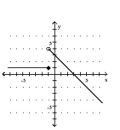
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
5
Classify the function as continuous or discontinuous. If the function is not continuous, identify the point(s)of
discontinuity.
-
A)discontinuous at x = 0
B)continuous
C)discontinuous at x = -2
D)discontinuous at x = 2
discontinuity.
-
A)discontinuous at x = 0
B)continuous
C)discontinuous at x = -2
D)discontinuous at x = 2

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
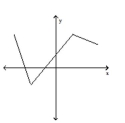
6
Classify the function as continuous or discontinuous.
A)continuous
B)discontinuous

A)continuous
B)discontinuous

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
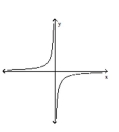
7
Classify the function as continuous or discontinuous.
A)discontinuous
B)continuous

A)discontinuous
B)continuous

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
8
Classify the function as continuous or discontinuous. If the function is not continuous, identify the point(s)of
discontinuity.
-
A)continuous
B)discontinuous at x = -3
C)
D)discontinuous at x = 3
discontinuity.
-
A)continuous
B)discontinuous at x = -3
C)
D)discontinuous at x = 3

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
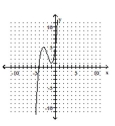
9
Identify the local maximum and minimum of the graphed function.
A)local maximum: (-1, 1)
B)local minimum: (-1, 1)local minimum: (-3, 5)local maximum: (-3, 5)
C)local minimum: (1, -1)
D)local maximum: (1, -1)local maximum: (5, -3)local minimum: (5, -3)

A)local maximum: (-1, 1)
B)local minimum: (-1, 1)local minimum: (-3, 5)local maximum: (-3, 5)
C)local minimum: (1, -1)
D)local maximum: (1, -1)local maximum: (5, -3)local minimum: (5, -3)

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
10
Classify the function as continuous or discontinuous. If the function is not continuous, identify the point(s)of
discontinuity.
-
A)continuous
B)discontinuous at x = -2 and x = 2
C)
D)discontinuous at x = 4
discontinuity.
-
A)continuous
B)discontinuous at x = -2 and x = 2
C)
D)discontinuous at x = 4

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
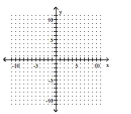
11
Graph the piecewise function.
-
A)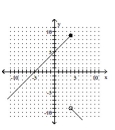
B)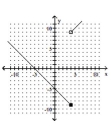
C)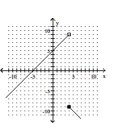
D)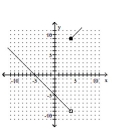
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
12
Classify the function as continuous or discontinuous. If the function is not continuous, identify the point(s)of
discontinuity.
-f(x)= 4x + 3
A)discontinuous at x = -3
B)
C)
D)continuous
discontinuity.
-f(x)= 4x + 3
A)discontinuous at x = -3
B)
C)
D)continuous

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
13
Classify the function as continuous or discontinuous. If the function is not continuous, identify the point(s)of
discontinuity.
-
A)discontinuous at x = . . . -3, -2, -1, 0, 1, 2, 3, . . .
B)continuous
C)
D)discontinuous at x = . . . -9, -6, -3, 0, 3, 6, 9, . . .
discontinuity.
-
A)discontinuous at x = . . . -3, -2, -1, 0, 1, 2, 3, . . .
B)continuous
C)
D)discontinuous at x = . . . -9, -6, -3, 0, 3, 6, 9, . . .

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
14
Classify the function as continuous or discontinuous. If the function is not continuous, identify the point(s)of
discontinuity.
-
A)discontinuous at x = -5
B)discontinuous at x = - 1
C)continuous
D)discontinuous at x = 5
discontinuity.
-
A)discontinuous at x = -5
B)discontinuous at x = - 1
C)continuous
D)discontinuous at x = 5

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
15
Classify the function as continuous or discontinuous.
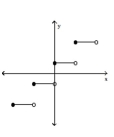
A)continuous
B)discontinuous

A)continuous
B)discontinuous

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
16
Classify the function as continuous or discontinuous. If the function is not continuous, identify the point(s)of
discontinuity.
-
A)discontinuous at x = 2
B)discontinuous at x = -2
C)continuous
D)discontinuous at x = 0
discontinuity.
-
A)discontinuous at x = 2
B)discontinuous at x = -2
C)continuous
D)discontinuous at x = 0

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
17
Classify the function as continuous or discontinuous.
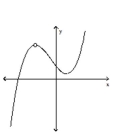
A)discontinuous
B)continuous

A)discontinuous
B)continuous

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
18
Classify the function as continuous or discontinuous. If the function is not continuous, identify the point(s)of
discontinuity.
-
A)continuous
B)discontinuous at x = 6
C)
D)discontinuous at x = -6
discontinuity.
-
A)continuous
B)discontinuous at x = 6
C)
D)discontinuous at x = -6

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
19
Classify the function as continuous or discontinuous. If the function is not continuous, identify the point(s)of
discontinuity.
-
A)discontinuous at x = 2 and x = 6
B)discontinuous at x = -2 and x = -6
C)continuous
D)
discontinuity.
-
A)discontinuous at x = 2 and x = 6
B)discontinuous at x = -2 and x = -6
C)continuous
D)

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
20
Graph the piecewise function.
-
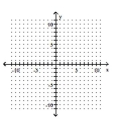
A)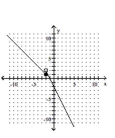
B)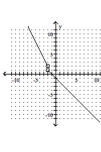
C)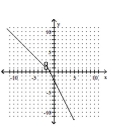
D)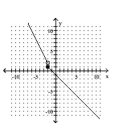
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
21
Graph the greatest integer function.
-
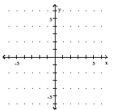
A)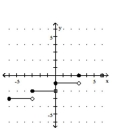
B)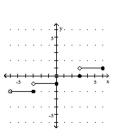
C)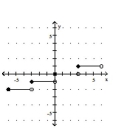
D)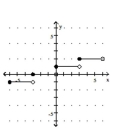
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
22
Graph the piecewise function.
-
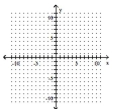
A)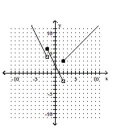
B)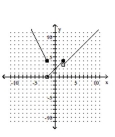
C)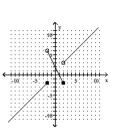
D)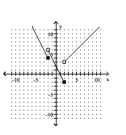
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
23
Find the real zeros of the function, state their multiplicities if it is a number other than 1.
-
A)x = 5, multiplicity: 2
B)
C)x = -5, multiplicity: 2
D)x = 5, x = -5
-
A)x = 5, multiplicity: 2
B)
C)x = -5, multiplicity: 2
D)x = 5, x = -5

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
24
Find the real zeros of the function, state their multiplicities if it is a number other than 1.
-
A)x = -8, multiplicity: 2
B)x = 8, multiplicity: 2
C)x = 16, multiplicity: 2
D)x = 8, x = -8
-
A)x = -8, multiplicity: 2
B)x = 8, multiplicity: 2
C)x = 16, multiplicity: 2
D)x = 8, x = -8

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
25
Determine whether the function is an even function, an odd function, or neither.
-
A)Odd
B)Even
C)Neither
-
A)Odd
B)Even
C)Neither

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
26
Find the real zeros of the function, state their multiplicities if it is a number other than 1.
-
A)x = 3, x = 4
B)x = 0, x = 3, x = 4
C)x = 0, x = - 5, x = 4
D)x = - 5, x = 4
-
A)x = 3, x = 4
B)x = 0, x = 3, x = 4
C)x = 0, x = - 5, x = 4
D)x = - 5, x = 4

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
27
Determine whether the function is an even function, an odd function, or neither.
-
A)Odd
B)Neither
C)Even
-
A)Odd
B)Neither
C)Even

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
28
Determine whether the function is an even function, an odd function, or neither.
-
A)Odd
B)Neither
C)Even
-
A)Odd
B)Neither
C)Even

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
29
Determine whether the function is an even function, an odd function, or neither.
-
A)Odd
B)Neither
C)Even
-
A)Odd
B)Neither
C)Even

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
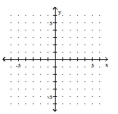
30
Graph the greatest integer function.
-
A)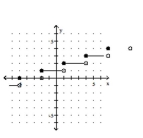
B)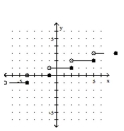
C)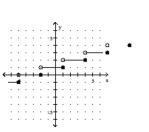
D)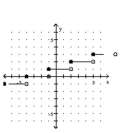
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the problem.
-Sam Wright wants to stock up on cans of cat food which are selling for $0.95 per can. Write a greatest integer function that represents the number of cans he can purchase with x dollars.
A)
B)
C)
D)
-Sam Wright wants to stock up on cans of cat food which are selling for $0.95 per can. Write a greatest integer function that represents the number of cans he can purchase with x dollars.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
32
Find the real zeros of the function, state their multiplicities if it is a number other than 1.
-
A)x = 3, x = 4
B)x = -3, x = 4
C)
D)
-
A)x = 3, x = 4
B)x = -3, x = 4
C)
D)

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
33
Find the real zeros of the function, state their multiplicities if it is a number other than 1.
-
A)
B)x = -13, x = 13
C)
D)x = 13, mutiplicity: 2
-
A)
B)x = -13, x = 13
C)
D)x = 13, mutiplicity: 2

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
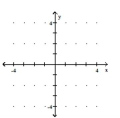
34
Graph the greatest integer function.
-
A)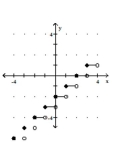
B)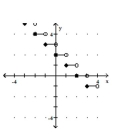
C)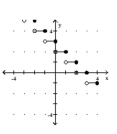
D)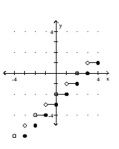
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
35
Find the real zeros of the function, state their multiplicities if it is a number other than 1.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the problem.
-A paddle boat rental company rents paddle boats by the hour. They charge $7.00 per hour for the first 3 rental hours and $5.00 per hour for each additional hour. Write a piecewise function to represent the cost of renting a
Paddle boat as a function of hours it is rented.
A)
B)
C)
D)
-A paddle boat rental company rents paddle boats by the hour. They charge $7.00 per hour for the first 3 rental hours and $5.00 per hour for each additional hour. Write a piecewise function to represent the cost of renting a
Paddle boat as a function of hours it is rented.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
37
Determine whether the function is an even function, an odd function, or neither.
-
A)Odd
B)Even
C)Neither
-
A)Odd
B)Even
C)Neither

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
38
Determine whether the function is an even function, an odd function, or neither.
-
A)Even
B)Neither
C)Odd
-
A)Even
B)Neither
C)Odd

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
39
Graph the piecewise function.
-
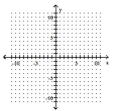
A)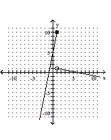
B)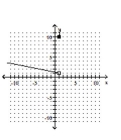
C)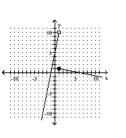
D)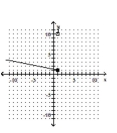
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
40
Determine whether the function is an even function, an odd function, or neither.
-
A)Even
B)Neither
C)Odd
-
A)Even
B)Neither
C)Odd

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
41
Find the real zeros of the function, state their multiplicities if it is a number other than 1.
-
A)
B)
C)
D) , multiplicity: 2
, multiplicity: 2
-
A)
B)
C)
D) , multiplicity: 2
, multiplicity: 2

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
42
Determine the maximum possible number of turning points for the graph of the function.
-
A)4
B)16
C)5
D)2
-
A)4
B)16
C)5
D)2

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
43
Find the x-intercepts of the function.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
44
Determine the maximum possible number of turning points for the graph of the function.
-
A)0
B)1
C)3
D)2
-
A)0
B)1
C)3
D)2

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
45
Find the real zeros of the function, state their multiplicities if it is a number other than 1.
-
A) , multiplicity: 2
, multiplicity: 3
B) , multiplicity: 2
, multiplicity: 3
C) , multiplicity: 2
, multiplicity: 2
D) , multiplicity: 2
, multiplicity: 3
-
A) , multiplicity: 2
, multiplicity: 3
B) , multiplicity: 2
, multiplicity: 3
C) , multiplicity: 2
, multiplicity: 2
D) , multiplicity: 2
, multiplicity: 3

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
46
Find the x-intercepts of the function.
-
A)x-intercept: (0, 0), x-intercept: (-5, 0)
B)x-intercept: (0, 0), x-intercept: (5, 0), x-intercept: (-5, 0)x-intercept: (4, 0), x-intercept: (-4, 0)
C)x-intercept: (0, 0), x-intercept: (5, 0)
D)x-intercept: (0, 0), x-intercept: (5, 0), x-intercept: (-5, 0)
-
A)x-intercept: (0, 0), x-intercept: (-5, 0)
B)x-intercept: (0, 0), x-intercept: (5, 0), x-intercept: (-5, 0)x-intercept: (4, 0), x-intercept: (-4, 0)
C)x-intercept: (0, 0), x-intercept: (5, 0)
D)x-intercept: (0, 0), x-intercept: (5, 0), x-intercept: (-5, 0)

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
47
Determine the maximum possible number of turning points for the graph of the function.
-
A)2
B)1
C)0
D)3
-
A)2
B)1
C)0
D)3

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
48
Find the x-intercepts of the function.
-
A)x-intercept: (1, 0), x-intercept: (-2, 0)x-intercept: (3, 0), x-intercept: (-3, 0)
B)x-intercept: (-1, 0), x-intercept: (2, 0)x-intercept: (3, 0), x-intercept: (-3, 0)
C)x-intercept: (-1, 0), x-intercept: (2, 0), x-intercept: (3, 0)
D)x-intercept: (-1, 0), x-intercept: (2, 0), x-intercept: (-3, 0)
-
A)x-intercept: (1, 0), x-intercept: (-2, 0)x-intercept: (3, 0), x-intercept: (-3, 0)
B)x-intercept: (-1, 0), x-intercept: (2, 0)x-intercept: (3, 0), x-intercept: (-3, 0)
C)x-intercept: (-1, 0), x-intercept: (2, 0), x-intercept: (3, 0)
D)x-intercept: (-1, 0), x-intercept: (2, 0), x-intercept: (-3, 0)

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
49
Find the x-intercepts of the function.
-
A)x-intercept: (9, 0)
B)x-intercept: (-9, 0)
C)x-intercept: (18, 0)
D)x-intercept: (9, 0), x-intercept: (-9, 0)
-
A)x-intercept: (9, 0)
B)x-intercept: (-9, 0)
C)x-intercept: (18, 0)
D)x-intercept: (9, 0), x-intercept: (-9, 0)

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
50
Find the x-intercepts of the function.
-
A)x-intercept: (12, 0)
B)
C)x-intercept: (-11, 0), x-intercept: (11, 0)
D)
-
A)x-intercept: (12, 0)
B)
C)x-intercept: (-11, 0), x-intercept: (11, 0)
D)

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
51
Find the x-intercepts of the function.
-
A)x-intercept: (8, 0)
B)
C)x-intercept: (8, 0), x-intercept: (-8, 0)
D)x-intercept: (-8, 0)
-
A)x-intercept: (8, 0)
B)
C)x-intercept: (8, 0), x-intercept: (-8, 0)
D)x-intercept: (-8, 0)

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
52
Find the x-intercepts of the function.
-
A)x-intercept: (-3, 0), x-intercept: (-1, 0)
B)
C)x-intercept: (1, 0), x-intercept: (2, 0)
D)x-intercept: (1, 0), x-intercept: (3, 0)
-
A)x-intercept: (-3, 0), x-intercept: (-1, 0)
B)
C)x-intercept: (1, 0), x-intercept: (2, 0)
D)x-intercept: (1, 0), x-intercept: (3, 0)

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
53
Determine the maximum possible number of turning points for the graph of the function.
-
A)2
B)3
C)1
D)6
-
A)2
B)3
C)1
D)6

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
54
Determine the maximum possible number of turning points for the graph of the function.
-
A)3
B)1
C)4
D)0
-
A)3
B)1
C)4
D)0

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
55
Find the x-intercepts of the function.
-
A)x-intercept: (0, 0), x-intercept: (- 6, 0), x-intercept: (5, 0)
B)x-intercept: (4, 0), x-intercept: (5, 0)
C)x-intercept: (- 6, 0), x-intercept: (5, 0)
D)x-intercept: (0, 0), x-intercept: (4, 0), x-intercept: (5, 0)
-
A)x-intercept: (0, 0), x-intercept: (- 6, 0), x-intercept: (5, 0)
B)x-intercept: (4, 0), x-intercept: (5, 0)
C)x-intercept: (- 6, 0), x-intercept: (5, 0)
D)x-intercept: (0, 0), x-intercept: (4, 0), x-intercept: (5, 0)

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
56
Find the real zeros of the function, state their multiplicities if it is a number other than 1.
-
A) , multiplicity: 2
B) , multiplicity: 2
C) , multiplicity: 2
, multiplicity: 2
D) , multiplicity: 2
, multiplicity: 2
-
A) , multiplicity: 2
B) , multiplicity: 2
C) , multiplicity: 2
, multiplicity: 2
D) , multiplicity: 2
, multiplicity: 2

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
57
Determine the maximum possible number of turning points for the graph of the function.
-
A)4
B)2
C)5
D)35
-
A)4
B)2
C)5
D)35

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
58
Determine the maximum possible number of turning points for the graph of the function.
-
A)3
B)4
C)0
D)2
-
A)3
B)4
C)0
D)2

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
59
Find the x-intercepts of the function.
-
A)x-intercept: (4, 0), x-intercept: (3, 0)
B)x-intercept: (4, 0), x-intercept: (-5, 0), x-intercept: (3, 0)
C)x-intercept: (-4, 0), x-intercept: (3, 0)
D)x-intercept: (-4, 0), x-intercept: (5, 0)
-
A)x-intercept: (4, 0), x-intercept: (3, 0)
B)x-intercept: (4, 0), x-intercept: (-5, 0), x-intercept: (3, 0)
C)x-intercept: (-4, 0), x-intercept: (3, 0)
D)x-intercept: (-4, 0), x-intercept: (5, 0)

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
60
Determine the maximum possible number of turning points for the graph of the function.
-
A)5
B)7
C)0
D)6
-
A)5
B)7
C)0
D)6

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
61
Determine which of the given graphs could be the graph of the given polynomial function.
-
A)
B)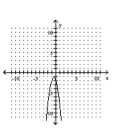
C)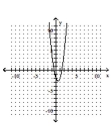
D)
-
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
62
Determine the minimum degree of the polynomial function graphed.
-

A)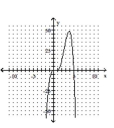
B)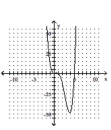
C)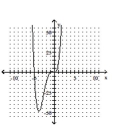
D)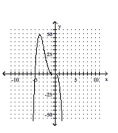
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
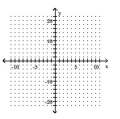
63
Determine the minimum degree of the polynomial function graphed.
-
A)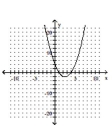
B)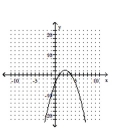
C)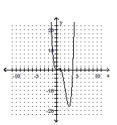
D)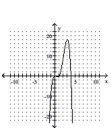
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
64
Determine the minimum degree of the polynomial function graphed.
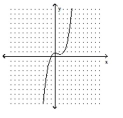
A)4
B)2
C)-3
D)3

A)4
B)2
C)-3
D)3

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
65
Describe the location, either above the x-axis or below the x-axis, of the graph of the function for large positive values of
x and for large negative values of x.
-
A)large positive values of x: below x-axis
B)large positive values of x: below x-axis large negative values of x: below x-axis large negative values of x: above x-axis
C)large positive values of x: above x-axis
D)large positive values of x: above x-axis large negative values of x: above x-axis large negative values of x: below x-axis
x and for large negative values of x.
-
A)large positive values of x: below x-axis
B)large positive values of x: below x-axis large negative values of x: below x-axis large negative values of x: above x-axis
C)large positive values of x: above x-axis
D)large positive values of x: above x-axis large negative values of x: above x-axis large negative values of x: below x-axis

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
66
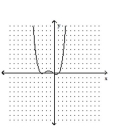
Determine the minimum degree of the polynomial function graphed.
A)2
B)3
C)4
D)-4

A)2
B)3
C)4
D)-4

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
67
Describe the location, either above the x-axis or below the x-axis, of the graph of the function for large positive values of
x and for large negative values of x.
-
A) large positive values of x: above x-axis , large negative values of x: above x-axis
B)llarge positive values of x: below x-axis , large negative values of x: above x-axis
C)large positive values of x: above x-axis , large negative values of x: below x-axis
D)large positive values of x: below x-axis , large negative values of x: below x-axis
x and for large negative values of x.
-
A) large positive values of x: above x-axis , large negative values of x: above x-axis
B)llarge positive values of x: below x-axis , large negative values of x: above x-axis
C)large positive values of x: above x-axis , large negative values of x: below x-axis
D)large positive values of x: below x-axis , large negative values of x: below x-axis

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
68
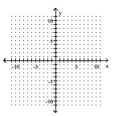
Determine the minimum degree of the polynomial function graphed.
-
A)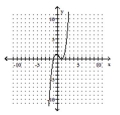
B)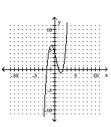
C)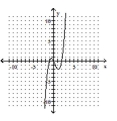
D)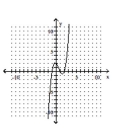
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
69
Determine which of the given graphs could be the graph of the given polynomial function.
-
A)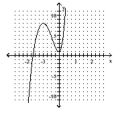
B)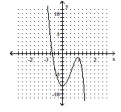
C)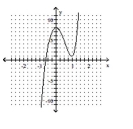
D)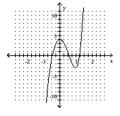
-
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
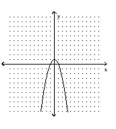
70
Determine the minimum degree of the polynomial function graphed.
A)2
B)4
C)3
D)-2

A)2
B)4
C)3
D)-2

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
71
Determine the maximum and minimum number of x-intercepts for the graph of the polynomial function. Do not graph
the function.
-
A)maximum number of x-intercepts: 9; minimum number of x-intercepts: 3
B)maximum number of x-intercepts: 9; minimum number of x-intercepts: 2
C)maximum number of x-intercepts: 9; minimum number of x-intercepts: 0
D)maximum number of x-intercepts: 9; minimum number of x-intercepts: 1
the function.
-
A)maximum number of x-intercepts: 9; minimum number of x-intercepts: 3
B)maximum number of x-intercepts: 9; minimum number of x-intercepts: 2
C)maximum number of x-intercepts: 9; minimum number of x-intercepts: 0
D)maximum number of x-intercepts: 9; minimum number of x-intercepts: 1

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
72
Determine the maximum and minimum number of x-intercepts for the graph of the polynomial function. Do not graph
the function.
-
A)maximum number of x-intercepts: 2; minimum number of x-intercepts: 1
B)maximum number of x-intercepts: 3; minimum number of x-intercepts: 3
C)maximum number of x-intercepts: 2; minimum number of x-intercepts: 2
D)maximum number of x-intercepts: 3; minimum number of x-intercepts: 2
the function.
-
A)maximum number of x-intercepts: 2; minimum number of x-intercepts: 1
B)maximum number of x-intercepts: 3; minimum number of x-intercepts: 3
C)maximum number of x-intercepts: 2; minimum number of x-intercepts: 2
D)maximum number of x-intercepts: 3; minimum number of x-intercepts: 2

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
73
Determine the minimum degree of the polynomial function graphed.
-
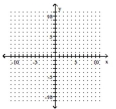
A)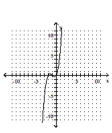
B)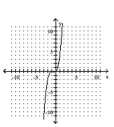
C)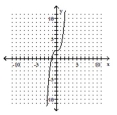
D)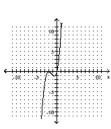
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
74
Determine the minimum degree of the polynomial function graphed.
-
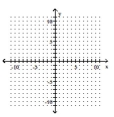
A)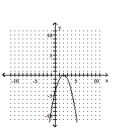
B)
C)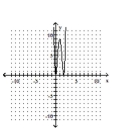
D)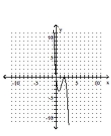
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
75
Determine the maximum and minimum number of x-intercepts for the graph of the polynomial function. Do not graph
the function.
-
A)maximum number of x-intercepts: 3; minimum number of x-intercepts: 0
B)maximum number of x-intercepts: 3; minimum number of x-intercepts: 1
C)maximum number of x-intercepts: 3; minimum number of x-intercepts: 2
D)maximum number of x-intercepts: 2; minimum number of x-intercepts: 1
the function.
-
A)maximum number of x-intercepts: 3; minimum number of x-intercepts: 0
B)maximum number of x-intercepts: 3; minimum number of x-intercepts: 1
C)maximum number of x-intercepts: 3; minimum number of x-intercepts: 2
D)maximum number of x-intercepts: 2; minimum number of x-intercepts: 1

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
76
Determine the minimum degree of the polynomial function graphed.
-
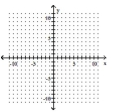
A)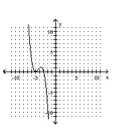
B)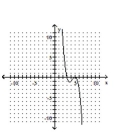
C)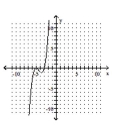
D)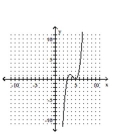
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
77
Determine the maximum and minimum number of x-intercepts for the graph of the polynomial function. Do not graph
the function.
-
A)maximum number of x-intercepts: 5; minimum number of x-intercepts: 2
B)maximum number of x-intercepts: 5; minimum number of x-intercepts: 0
C)maximum number of x-intercepts: 6; minimum number of x-intercepts: 0
D)maximum number of x-intercepts: 6; minimum number of x-intercepts: 2
the function.
-
A)maximum number of x-intercepts: 5; minimum number of x-intercepts: 2
B)maximum number of x-intercepts: 5; minimum number of x-intercepts: 0
C)maximum number of x-intercepts: 6; minimum number of x-intercepts: 0
D)maximum number of x-intercepts: 6; minimum number of x-intercepts: 2

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
78
Determine the minimum degree of the polynomial function graphed.
-

A)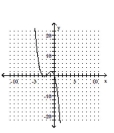
B)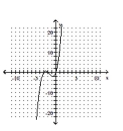
C)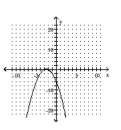
D)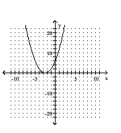
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
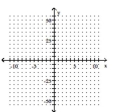
79
Determine the minimum degree of the polynomial function graphed.
-
A)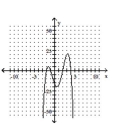
B)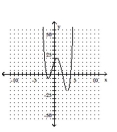
C)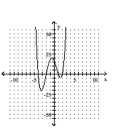
D)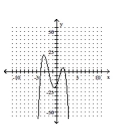
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck
80
Describe the location, either above the x-axis or below the x-axis, of the graph of the function for large positive values of
x and for large negative values of x.
-
A)large positive values of x: above x-axis
B)large positive values of x: below x-axis large negative values of x: below x-axis large negative values of x: below x-axis
C)large positive values of x: below x-axis
D)large positive values of x: above x-axis large negative values of x: above x-axis large negative values of x: above x-axis
x and for large negative values of x.
-
A)large positive values of x: above x-axis
B)large positive values of x: below x-axis large negative values of x: below x-axis large negative values of x: below x-axis
C)large positive values of x: below x-axis
D)large positive values of x: above x-axis large negative values of x: above x-axis large negative values of x: above x-axis

Unlock Deck
Unlock for access to all 142 flashcards in this deck.
Unlock Deck
k this deck


