Exam 10: Characteristics of Functions and Their Graphs
Exam 1: Basic Concepts306 Questions
Exam 2: Equations and Inequalities234 Questions
Exam 3: Graphs and Functions61 Questions
Exam 4: Systems of Equations and Inequalities116 Questions
Exam 5: Polynomials and Polynomial Functions112 Questions
Exam 6: Rational Expressions and Equations130 Questions
Exam 7: Roots, Radicals, and Complex Numbers298 Questions
Exam 8: Quadratic Functions221 Questions
Exam 9: Exponential and Logarithmic Functions229 Questions
Exam 10: Characteristics of Functions and Their Graphs142 Questions
Exam 11: Conic Sections132 Questions
Exam 12: Sequences, Series, and Probability208 Questions
Select questions type
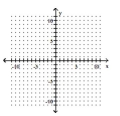
Determine the minimum degree of the polynomial function graphed.
-
Free
(Multiple Choice)
4.8/5  (32)
(32)
Correct Answer:
D
Determine the maximum possible number of turning points for the graph of the function.
-
Free
(Multiple Choice)
4.9/5  (40)
(40)
Correct Answer:
C
Determine the maximum and minimum number of x-intercepts for the graph of the polynomial function. Do not graph
the function.
-
Free
(Multiple Choice)
4.8/5  (34)
(34)
Correct Answer:
D
Determine whether the graph of the rational function has a horizontal asymptote, an oblique asymptote, or neither. Give
the equation of the asymptote if it exists.
-
(Multiple Choice)
4.7/5  (40)
(40)
Find the real zeros of the function, state their multiplicities if it is a number other than 1.
-
(Multiple Choice)
4.8/5  (34)
(34)
Determine whether the function is an even function, an odd function, or neither.
-
(Multiple Choice)
4.8/5  (38)
(38)
Determine whether the graph of the rational function has a horizontal asymptote, an oblique asymptote, or neither. Give
the equation of the asymptote if it exists.
-
(Multiple Choice)
4.8/5  (30)
(30)
Determine the maximum possible number of turning points for the graph of the function.
-
(Multiple Choice)
4.8/5  (38)
(38)
Determine whether the function is an even function, an odd function, or neither.
-
(Multiple Choice)
4.7/5  (27)
(27)
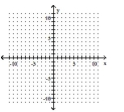
Determine the minimum degree of the polynomial function graphed.
-
(Multiple Choice)
4.9/5  (32)
(32)
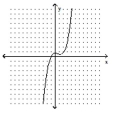
Determine the minimum degree of the polynomial function graphed.
-
(Multiple Choice)
4.8/5  (46)
(46)
Classify the function as continuous or discontinuous. If the function is not continuous, identify the point(s)of
discontinuity.
-f(x)= 4x + 3
(Multiple Choice)
4.8/5  (28)
(28)
Determine the maximum and minimum number of x-intercepts for the graph of the polynomial function. Do not graph
the function.
-
(Multiple Choice)
4.9/5  (48)
(48)
Describe the location, either above the x-axis or below the x-axis, of the graph of the function for large positive values of
x and for large negative values of x.
-
(Multiple Choice)
4.9/5  (39)
(39)
Determine the maximum possible number of turning points for the graph of the function.
-
(Multiple Choice)
4.9/5  (32)
(32)
Find all points of discontinuity, and determine whether there is a hole or a vertical asymptote at each point.
-
(Multiple Choice)
5.0/5  (32)
(32)
Determine the maximum possible number of turning points for the graph of the function.
-
(Multiple Choice)
4.8/5  (36)
(36)
Showing 1 - 20 of 142
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)