Deck 12: Inference About Comparing Two Populat
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/85
Play
Full screen (f)
Deck 12: Inference About Comparing Two Populat
1
Independent samples are those for which the selection process for one is not related to the selection process for the other.
True
2
In comparing the difference in means with a matched pairs experiment, the variable under consideration is 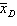 , where the subscript D refers to the difference.
, where the subscript D refers to the difference.
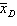 , where the subscript D refers to the difference.
, where the subscript D refers to the difference.True
3
A political analyst in Iowa surveys a random sample of registered Republicans and compares the results with those obtained from a random sample of registered Democrats . This would be an example of two independent samples.
True
4
The sampling distribution of 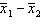 is normal if the sampled populations are normal, and approximately normal if the populations are nonnormal and the sample sizes n 1 and n 2 are large.
is normal if the sampled populations are normal, and approximately normal if the populations are nonnormal and the sample sizes n 1 and n 2 are large.
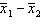 is normal if the sampled populations are normal, and approximately normal if the populations are nonnormal and the sample sizes n 1 and n 2 are large.
is normal if the sampled populations are normal, and approximately normal if the populations are nonnormal and the sample sizes n 1 and n 2 are large.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
5
The pooled-variances t -test requires that the two population variances need not be the same.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
6
A matched pairs experiment decreases variability (compared to two independent samples).

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
7
Two samples of sizes 25 and 20 are independently drawn from two normal populations, where the unknown population variances are assumed to be equal. The number of degrees of freedom of the equal-variances t -test statistic is 44.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
8
The best estimator of the difference between two population means 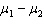 is the difference between two sample means
is the difference between two sample means 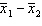 .
.
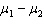 is the difference between two sample means
is the difference between two sample means 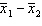 .
.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
9
A calculus professor wanted to test whether the grades on calculus test were the same for upper and lower classmen. The professor took a random sample of size 12 from each group. For this situation, the professor should use a matched pairs t -test.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
10
When the population variances are unequal, we estimate each population variance with its sample variance. Hence, the unequal-variances test statistic of 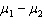 is approximately Student t -distributed with n 1 + n 2 - 2 degrees of freedom.
is approximately Student t -distributed with n 1 + n 2 - 2 degrees of freedom.
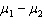 is approximately Student t -distributed with n 1 + n 2 - 2 degrees of freedom.
is approximately Student t -distributed with n 1 + n 2 - 2 degrees of freedom.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
11
When the sample sizes are equal, the pooled variance of the two samples is the average of the two sample variances.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
12
Unless we can conclude that the population variances are equal, we cannot use the pooled variance estimate.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
13
Two measurements from the same individuals is an example of data collected from a matched pairs experiment.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
14
Both the equal-variances and unequal variances test statistic and confidence interval estimator of 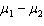 require that the two populations be normally distributed.
require that the two populations be normally distributed.
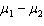 require that the two populations be normally distributed.
require that the two populations be normally distributed.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
15
In testing the difference between two population means using two independent samples, the sampling distribution of the sample mean difference 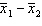 is normal if the sample sizes are both greater than 30.
is normal if the sample sizes are both greater than 30.
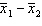 is normal if the sample sizes are both greater than 30.
is normal if the sample sizes are both greater than 30.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
16
The expected value of 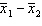 is
is 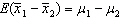 .
.
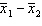 is
is 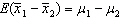 .
.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
17
In testing the difference between two population means using two independent samples, we use the pooled variance in estimating the standard error of the sampling distribution of the sample mean difference 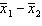 if the populations are normal with equal variances.
if the populations are normal with equal variances.
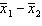 if the populations are normal with equal variances.
if the populations are normal with equal variances.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
18
The variance of 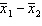 is
is 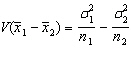 .
.
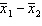 is
is 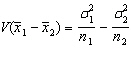 .
.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
19
When we test for differences between the means of two independent populations, we can only use a two-tailed test.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
20
The equal-variances test statistic of 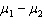 is Student t -distributed with n 1 + n 2 degrees of freedom, provided that the two populations are normal.
is Student t -distributed with n 1 + n 2 degrees of freedom, provided that the two populations are normal.
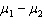 is Student t -distributed with n 1 + n 2 degrees of freedom, provided that the two populations are normal.
is Student t -distributed with n 1 + n 2 degrees of freedom, provided that the two populations are normal.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
21
In testing the difference between the means of two normally distributed populations, the number of degrees of freedom associated with the unequal-variances t- test statistic usually results in a non-integer number. It is recommended that you:
A)round to the nearest integer.
B)change the sample sizes until the number of degrees of freedom becomes an integer.
C)assume that the population variances are equal, and then use df = n 1 + n 2 - 2.
D)None of these choices.
A)round to the nearest integer.
B)change the sample sizes until the number of degrees of freedom becomes an integer.
C)assume that the population variances are equal, and then use df = n 1 + n 2 - 2.
D)None of these choices.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
22
When testing 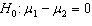 vs.
vs. 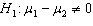 , the observed value of the z -score was found to be - 2.15. Then, the p -value for this test would be
, the observed value of the z -score was found to be - 2.15. Then, the p -value for this test would be
A).0158
B).0316
C).9842
D).9684
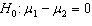 vs.
vs. 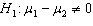 , the observed value of the z -score was found to be - 2.15. Then, the p -value for this test would be
, the observed value of the z -score was found to be - 2.15. Then, the p -value for this test would beA).0158
B).0316
C).9842
D).9684

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
23
If there are 10 pairs of data in a matched pairs experiment, the degrees of freedom for the corresponding t -test is 18.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
24
Two independent samples of sizes 20 and 30 are randomly selected from two normally distributed populations. Assume that the population variances are unknown but equal. In order to test the difference between the population means, 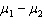 , the sampling distribution of the sample mean difference,
, the sampling distribution of the sample mean difference, 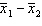 , is:
, is:
A)normal.
B)Student -t with 50 degrees of freedom.
C)Student -t with 48 degrees of freedom.
D)None of these choices.
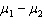 , the sampling distribution of the sample mean difference,
, the sampling distribution of the sample mean difference, 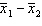 , is:
, is:A)normal.
B)Student -t with 50 degrees of freedom.
C)Student -t with 48 degrees of freedom.
D)None of these choices.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
25
The number of degrees of freedom associated with the t -test, when the data are gathered from a matched pairs experiment with 8 pairs, is 7.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
26
The expected value of the difference of two sample means equals the difference of the corresponding population means when:
A)the populations are normally distributed.
B)the samples are independent.
C)the populations are approximately normal and the sample sizes are large.
D)All of these choices are true.
A)the populations are normally distributed.
B)the samples are independent.
C)the populations are approximately normal and the sample sizes are large.
D)All of these choices are true.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
27
In comparing two population means of interval data, we must decide whether the samples are independent (in which case the parameter of interest is 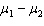 )or matched pairs (in which case the parameter is m D )in order to select the correct test statistic.
)or matched pairs (in which case the parameter is m D )in order to select the correct test statistic.
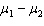 )or matched pairs (in which case the parameter is m D )in order to select the correct test statistic.
)or matched pairs (in which case the parameter is m D )in order to select the correct test statistic.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
28
The quantity 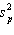 is called the pooled variance estimate of the common variance of two unknown but equal population variances. It is the weighted average of the two sample variances, where the weights represent the:
is called the pooled variance estimate of the common variance of two unknown but equal population variances. It is the weighted average of the two sample variances, where the weights represent the:
A)sample variances.
B)sample standard deviations.
C)degrees of freedom for each sample.
D)None of these choices.
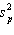 is called the pooled variance estimate of the common variance of two unknown but equal population variances. It is the weighted average of the two sample variances, where the weights represent the:
is called the pooled variance estimate of the common variance of two unknown but equal population variances. It is the weighted average of the two sample variances, where the weights represent the:A)sample variances.
B)sample standard deviations.
C)degrees of freedom for each sample.
D)None of these choices.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
29
Two independent samples of sizes 40 and 50 are randomly selected from two populations to test the difference between the population means 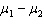 . Assume the population variances are known. The sampling distribution of the sample mean difference
. Assume the population variances are known. The sampling distribution of the sample mean difference 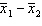 is:
is:
A)normally distributed.
B)approximately normal.
C)Student t- distributed with 88 degrees of freedom.
D)None of these choices.
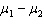 . Assume the population variances are known. The sampling distribution of the sample mean difference
. Assume the population variances are known. The sampling distribution of the sample mean difference 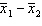 is:
is:A)normally distributed.
B)approximately normal.
C)Student t- distributed with 88 degrees of freedom.
D)None of these choices.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
30
In testing for the differences between the means of two independent populations where the variances in each population are unknown but assumed equal, the degrees of freedom is:
A)n 1 + n 2
B)n 1 + n 2 - 2
C)n 1 + n 2 - 1
D)None of these choices
A)n 1 + n 2
B)n 1 + n 2 - 2
C)n 1 + n 2 - 1
D)None of these choices

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
31
Two independent samples of sizes 25 and 35 are randomly selected from two normal populations with equal variances (assumed to be unknown). In order to test the difference between the population means, the test statistic is:
A)a standard normal random variable.
B)approximately standard normal random variable.
C)Student t- distributed with 58 degrees of freedom.
D)Student t- distributed with 33 degrees of freedom.
A)a standard normal random variable.
B)approximately standard normal random variable.
C)Student t- distributed with 58 degrees of freedom.
D)Student t- distributed with 33 degrees of freedom.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
32
In constructing a confidence interval estimate for the difference between the means of two independent normally distributed populations, we:
A)pool the sample variances when the unknown population variances are equal.
B)pool the sample variances when the population variances are known and equal.
C)pool the sample variances when the population means are equal.
D)never pool the sample variances.
A)pool the sample variances when the unknown population variances are equal.
B)pool the sample variances when the population variances are known and equal.
C)pool the sample variances when the population means are equal.
D)never pool the sample variances.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
33
If we are testing for the difference between the means of two independent populations with equal variances, samples of n 1 = 15 and n 2 = 15 are taken, then the number of degrees of freedom is equal to
A)13
B)14
C)28
D)29
A)13
B)14
C)28
D)29

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
34
In testing the difference between two population means for which the population variances are unknown and not assumed to be equal, two independent samples are drawn from the populations. Which of the following tests is appropriate?
A)z -test
B)pooled-variances t -test
C)unequal variances t -test
D)None of these choices.
A)z -test
B)pooled-variances t -test
C)unequal variances t -test
D)None of these choices.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
35
When comparing two population means using data that are gathered from a matched pairs experiment, the test statistic for m D is Student t -distributed with v = nD - 1 degrees of freedom, provided that the differences are normally distributed.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
36
In testing the difference between two population means using two independent samples, we use the pooled variance in estimating the standard error of the sampling distribution of the sample mean difference 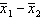 if:
if:
A)the sample sizes are both large.
B)the populations are normal with equal variances.
C)the populations are non-normal with unequal variances.
D)All of these choices are true.
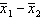 if:
if:A)the sample sizes are both large.
B)the populations are normal with equal variances.
C)the populations are non-normal with unequal variances.
D)All of these choices are true.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
37
In testing the difference between the means of two normal populations using two independent samples when the population variances are unequal, the sampling distribution of the resulting statistic is:
A)normal.
B)Student- t .
C)approximately normal.
D)approximately Student- t .
A)normal.
B)Student- t .
C)approximately normal.
D)approximately Student- t .

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
38
A Marine boot camp instructor recorded the time in which each of 15 recruits completed an obstacle course both before and after basic training. To test whether any improvement occurred, the instructor would use a t -distribution with 15 degrees of freedom.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
39
Given the information: 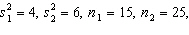 the number of degrees of freedom that should be used in the pooled variance t -test is:
the number of degrees of freedom that should be used in the pooled variance t -test is:
A)40
B)38
C)15
D)25
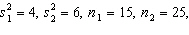 the number of degrees of freedom that should be used in the pooled variance t -test is:
the number of degrees of freedom that should be used in the pooled variance t -test is:A)40
B)38
C)15
D)25

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
40
The t -test for the difference between the means of two independent populations assumes that the respective:
A)sample sizes are equal.
B)populations are normal.
C)means are equal.
D)All of these choices are true.
A)sample sizes are equal.
B)populations are normal.
C)means are equal.
D)All of these choices are true.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
41
The test for the mean difference in a matched pairs design requires the differences to have a(n)____________________ distribution.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
42
The degrees of freedom for a test of the mean of the paired differences is the number of ____________________ minus ____________________.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
43
____________________ samples are those for which the selection process for one is not related to the selection process for the other.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
44
A test is being conducted to test the difference between two population means using data that are gathered from a matched pairs experiment. If the paired differences are normal, then the distribution used for testing is the:
A)normal distribution.
B)binomial distribution.
C)Student t -distribution.
D)F -distribution.
A)normal distribution.
B)binomial distribution.
C)Student t -distribution.
D)F -distribution.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
45
The unequal-variances test statistic of 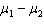 has an approximate ____________________ distribution with n 1 + n 2 - 2 degrees of freedom.
has an approximate ____________________ distribution with n 1 + n 2 - 2 degrees of freedom.
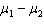 has an approximate ____________________ distribution with n 1 + n 2 - 2 degrees of freedom.
has an approximate ____________________ distribution with n 1 + n 2 - 2 degrees of freedom.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
46
The pooled-variances t -test is used when the two population variances are ____________________.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
47
The number of degrees of freedom associated with the t -test, when the data are gathered from a matched pairs experiment with 10 pairs, is:
A)10
B)20
C)9
D)18
A)10
B)20
C)9
D)18

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
48
The symbol 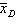 refers to:
refers to:
A)the difference in the means of two independent populations.
B)one matched pairs difference.
C)the mean difference in the pairs of observations.
D)None of these choices.
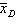 refers to:
refers to:A)the difference in the means of two independent populations.
B)one matched pairs difference.
C)the mean difference in the pairs of observations.
D)None of these choices.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
49
A political analyst in Hawaii surveys a random sample of registered Democrats and compares the results with those obtained from a random sample of registered Republicans. This would be an example of:
A)independent samples.
B)dependent samples.
C)independent samples only if the sample sizes are equal.
D)dependent samples only if the sample sizes are equal.
A)independent samples.
B)dependent samples.
C)independent samples only if the sample sizes are equal.
D)dependent samples only if the sample sizes are equal.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
50
A political analyst in Iowa surveys a random sample of registered Democrats and compares the results with those obtained from a random sample of registered Republicans. This would be an example of ____________________ samples.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
51
In testing for a mean difference the null hypothesis is:
A)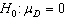
B)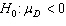
C)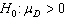
D)None of these choices.
A)
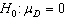
B)
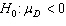
C)
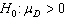
D)None of these choices.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
52
When two population variances are ____________________ we estimate each population variance with its sample variance. The test statistic of 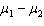 is approximately Student t -distributed with n 1 + n 2 - 2 degrees of freedom.
is approximately Student t -distributed with n 1 + n 2 - 2 degrees of freedom.
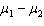 is approximately Student t -distributed with n 1 + n 2 - 2 degrees of freedom.
is approximately Student t -distributed with n 1 + n 2 - 2 degrees of freedom.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
53
Suppose we randomly selected 250 people, and on the basis of their responses to a survey we assigned them to one of two groups: high-risk group and low-risk group. We then recorded the blood pressure for the members of each group. Such data are called:
A)observational.
B)experimental.
C)matched.
D)None of these choices.
A)observational.
B)experimental.
C)matched.
D)None of these choices.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
54
When the population variances are unknown and unequal, we estimate each population variance with its ____________________ variance.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
55
In testing for differences between the means of two independent populations the null hypothesis is:
A)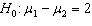
B)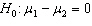
C)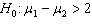
D)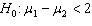
A)
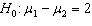
B)
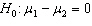
C)
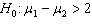
D)

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
56
Two measurements from the same individuals is an example of data collected from a(n)____________________ experiment.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
57
If some natural relationship exists between each pair of observations that provides a logical reason to compare the first observation of sample 1 with the first observation of sample 2, the second observation of sample 1 with the second observation of sample 2, and so on, the samples are referred to as:
A)matched pairs.
B)independent samples.
C)nonrandom samples.
D)None of these choices.
A)matched pairs.
B)independent samples.
C)nonrandom samples.
D)None of these choices.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
58
When the sample sizes are equal, the pooled variance of the two samples is the ____________________ of the two sample variances.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
59
The pooled variance estimator is the ____________________ average of the two sample variances.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
60
The equal-variances test statistic of 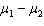 is Student t -distributed with n 1 + n 2 - 2 degrees of freedom provided that the two populations are ____________________.
is Student t -distributed with n 1 + n 2 - 2 degrees of freedom provided that the two populations are ____________________.
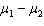 is Student t -distributed with n 1 + n 2 - 2 degrees of freedom provided that the two populations are ____________________.
is Student t -distributed with n 1 + n 2 - 2 degrees of freedom provided that the two populations are ____________________.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
61
Aptitude Test Scores Two random samples of 40 students were drawn independently from two populations of students. Assume their aptitude tests are normally distributed (total points = 100). The following statistics regarding their scores in an aptitude test were obtained: 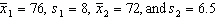 . {Aptitude Test Scores Narrative} Test at the 5% significance level to determine whether we can infer that the two population means differ.
. {Aptitude Test Scores Narrative} Test at the 5% significance level to determine whether we can infer that the two population means differ.
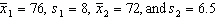 . {Aptitude Test Scores Narrative} Test at the 5% significance level to determine whether we can infer that the two population means differ.
. {Aptitude Test Scores Narrative} Test at the 5% significance level to determine whether we can infer that the two population means differ.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
62
Undergraduates' Test Scores 35 undergraduate students who completed two years of college were asked to take a basic mathematics test. The mean and standard deviation of their scores were 75.1 and 12.8, respectively. In a random sample of 50 students who only completed high school, the mean and standard deviation of the test scores were 72.1 and 14.6, respectively {Undergraduates' Test Scores Narrative} Can we infer at the 10% significance level that a difference exists between the two groups?

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
63
Promotional Campaigns The general manager of a chain of fast food chicken restaurants wants to determine how effective their promotional campaigns are. In these campaigns "20% off" coupons are widely distributed. These coupons are only valid for one week. To examine their effectiveness, the executive records the daily gross sales (in $1,000s)in one restaurant during the campaign and during the week after the campaign ends. The data is shown below.
Day Sales During Campaign Sales After Campaign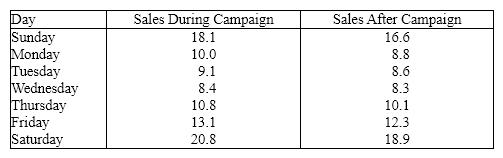 {Promotional Campaigns Narrative} Can they infer at the 5% significance level that sales increase during the campaign?
{Promotional Campaigns Narrative} Can they infer at the 5% significance level that sales increase during the campaign?
Day Sales During Campaign Sales After Campaign
 {Promotional Campaigns Narrative} Can they infer at the 5% significance level that sales increase during the campaign?
{Promotional Campaigns Narrative} Can they infer at the 5% significance level that sales increase during the campaign?
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
64
The service manager of a car dealer wants to determine if owners of new cars (two years old or less)tune up their cars more frequently than owners of older cars (more than two years old). From his records he takes a random sample of ten new cars and ten older cars and determines the number of times the cars were tuned up in the last 12 months. The data follow. Do these data allow the service station owner to infer at the 10% significance level that new car owners tune up their cars more frequently than older car owners? 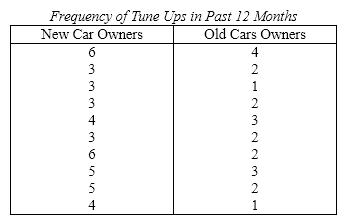


Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
65
If you are testing to see if a weight loss program is working, and you subtract the weights before - after for a group of 10 people, the alternative hypothesis is that the mean difference is ____________________ 0.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
66
In a matched pairs experiment the parameter of interest is the ____________________ of the population of ____________________.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
67
Aptitude Test Scores Two random samples of 40 students were drawn independently from two populations of students. Assume their aptitude tests are normally distributed (total points = 100). The following statistics regarding their scores in an aptitude test were obtained: 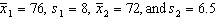 . {Aptitude Test Scores Narrative} Estimate with 95% confidence the difference between the two population means.
. {Aptitude Test Scores Narrative} Estimate with 95% confidence the difference between the two population means.
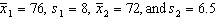 . {Aptitude Test Scores Narrative} Estimate with 95% confidence the difference between the two population means.
. {Aptitude Test Scores Narrative} Estimate with 95% confidence the difference between the two population means.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
68
Additives A food processor wants to compare two additives for their effects on retarding spoilage. Suppose 16 cuts of fresh meat are treated with additive A and 16 are treated with additive B, and the number of hours until spoilage begins is recorded for each of the 32 cuts of meat. The results are summarized in the table below  {Additives Narrative} Determine the rejection region at a = .05 and write the proper conclusion.
{Additives Narrative} Determine the rejection region at a = .05 and write the proper conclusion.
 {Additives Narrative} Determine the rejection region at a = .05 and write the proper conclusion.
{Additives Narrative} Determine the rejection region at a = .05 and write the proper conclusion.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
69
Additives A food processor wants to compare two additives for their effects on retarding spoilage. Suppose 16 cuts of fresh meat are treated with additive A and 16 are treated with additive B, and the number of hours until spoilage begins is recorded for each of the 32 cuts of meat. The results are summarized in the table below  {Additives Narrative} Assume population variances are equal. Calculate the pooled variance and the value of the test statistic.
{Additives Narrative} Assume population variances are equal. Calculate the pooled variance and the value of the test statistic.
 {Additives Narrative} Assume population variances are equal. Calculate the pooled variance and the value of the test statistic.
{Additives Narrative} Assume population variances are equal. Calculate the pooled variance and the value of the test statistic.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
70
In testing the hypothesis 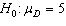 vs.
vs. 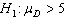 , two random samples from two normal populations produced the following statistics:
, two random samples from two normal populations produced the following statistics: 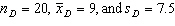 . What conclusion can we draw at the 1% significance level?
. What conclusion can we draw at the 1% significance level?
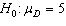 vs.
vs. 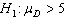 , two random samples from two normal populations produced the following statistics:
, two random samples from two normal populations produced the following statistics: 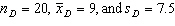 . What conclusion can we draw at the 1% significance level?
. What conclusion can we draw at the 1% significance level?
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
71
Starting Salary In testing the hypotheses 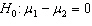 vs.
vs. 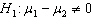 , two random samples from two populations of college of business graduates majoring in global marketing and international business produced the following statistics regarding their starting salaries (in $1000s):
, two random samples from two populations of college of business graduates majoring in global marketing and international business produced the following statistics regarding their starting salaries (in $1000s): 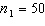 ,
, 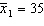 ,
, 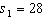 ,
, 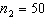 ,
, 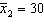 , and
, and 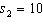 . (Assume the salaries have normal distributions.){Starting Salary Narrative} What conclusion can we draw at the 5% significance level?
. (Assume the salaries have normal distributions.){Starting Salary Narrative} What conclusion can we draw at the 5% significance level?
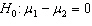 vs.
vs. 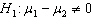 , two random samples from two populations of college of business graduates majoring in global marketing and international business produced the following statistics regarding their starting salaries (in $1000s):
, two random samples from two populations of college of business graduates majoring in global marketing and international business produced the following statistics regarding their starting salaries (in $1000s): 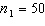 ,
, 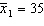 ,
, 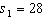 ,
, 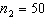 ,
, 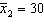 , and
, and 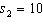 . (Assume the salaries have normal distributions.){Starting Salary Narrative} What conclusion can we draw at the 5% significance level?
. (Assume the salaries have normal distributions.){Starting Salary Narrative} What conclusion can we draw at the 5% significance level?
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
72
Starting Salary In testing the hypotheses 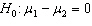 vs.
vs. 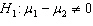 , two random samples from two populations of college of business graduates majoring in global marketing and international business produced the following statistics regarding their starting salaries (in $1000s):
, two random samples from two populations of college of business graduates majoring in global marketing and international business produced the following statistics regarding their starting salaries (in $1000s): 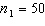 ,
, 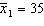 ,
, 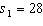 ,
, 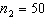 ,
, 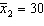 , and
, and 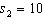 . (Assume the salaries have normal distributions.){Starting Salary Narrative} Explain how to use the 95% confidence interval to test the hypotheses at a = .05.
. (Assume the salaries have normal distributions.){Starting Salary Narrative} Explain how to use the 95% confidence interval to test the hypotheses at a = .05.
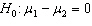 vs.
vs. 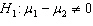 , two random samples from two populations of college of business graduates majoring in global marketing and international business produced the following statistics regarding their starting salaries (in $1000s):
, two random samples from two populations of college of business graduates majoring in global marketing and international business produced the following statistics regarding their starting salaries (in $1000s): 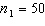 ,
, 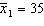 ,
, 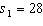 ,
, 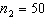 ,
, 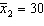 , and
, and 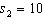 . (Assume the salaries have normal distributions.){Starting Salary Narrative} Explain how to use the 95% confidence interval to test the hypotheses at a = .05.
. (Assume the salaries have normal distributions.){Starting Salary Narrative} Explain how to use the 95% confidence interval to test the hypotheses at a = .05.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
73
Starting Salary In testing the hypotheses 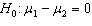 vs.
vs. 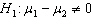 , two random samples from two populations of college of business graduates majoring in global marketing and international business produced the following statistics regarding their starting salaries (in $1000s):
, two random samples from two populations of college of business graduates majoring in global marketing and international business produced the following statistics regarding their starting salaries (in $1000s): 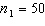 ,
, 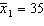 ,
, 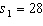 ,
, 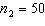 ,
, 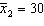 , and
, and 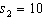 . (Assume the salaries have normal distributions.){Starting Salary Narrative} Estimate with 95% confidence the difference between the two population means.
. (Assume the salaries have normal distributions.){Starting Salary Narrative} Estimate with 95% confidence the difference between the two population means.
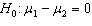 vs.
vs. 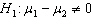 , two random samples from two populations of college of business graduates majoring in global marketing and international business produced the following statistics regarding their starting salaries (in $1000s):
, two random samples from two populations of college of business graduates majoring in global marketing and international business produced the following statistics regarding their starting salaries (in $1000s): 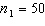 ,
, 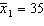 ,
, 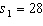 ,
, 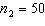 ,
, 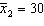 , and
, and 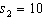 . (Assume the salaries have normal distributions.){Starting Salary Narrative} Estimate with 95% confidence the difference between the two population means.
. (Assume the salaries have normal distributions.){Starting Salary Narrative} Estimate with 95% confidence the difference between the two population means.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
74
If you are testing to see if a weight loss program is working, and you subtract the weights after - before for a group of 10 people, the alternative hypothesis is that the mean difference is ____________________ 0.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
75
Engine Wear To compare the wearing of two types of automobile engines, 1 and 2, an experimenter chose to "pair" the measurements, comparing the wear for the two types of engines on each of 7 automobiles, as shown below.  (Engine Wear Narrative} Determine whether these data are sufficient to infer at the 10% significance level that the two types of engines wear differently.
(Engine Wear Narrative} Determine whether these data are sufficient to infer at the 10% significance level that the two types of engines wear differently.
 (Engine Wear Narrative} Determine whether these data are sufficient to infer at the 10% significance level that the two types of engines wear differently.
(Engine Wear Narrative} Determine whether these data are sufficient to infer at the 10% significance level that the two types of engines wear differently.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
76
Undergraduates' Test Scores 35 undergraduate students who completed two years of college were asked to take a basic mathematics test. The mean and standard deviation of their scores were 75.1 and 12.8, respectively. In a random sample of 50 students who only completed high school, the mean and standard deviation of the test scores were 72.1 and 14.6, respectively {Undergraduates' Test Scores Narrative} Estimate with 90% confidence the difference in mean scores between the two groups of students.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
77
Promotional Campaigns The general manager of a chain of fast food chicken restaurants wants to determine how effective their promotional campaigns are. In these campaigns "20% off" coupons are widely distributed. These coupons are only valid for one week. To examine their effectiveness, the executive records the daily gross sales (in $1,000s)in one restaurant during the campaign and during the week after the campaign ends. The data is shown below.
Day Sales During Campaign Sales After Campaign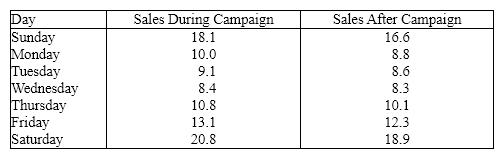 {Promotional Campaigns Narrative} Estimate with 95% confidence the mean difference and interpret.
{Promotional Campaigns Narrative} Estimate with 95% confidence the mean difference and interpret.
Day Sales During Campaign Sales After Campaign
 {Promotional Campaigns Narrative} Estimate with 95% confidence the mean difference and interpret.
{Promotional Campaigns Narrative} Estimate with 95% confidence the mean difference and interpret.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
78
Aptitude Test Scores Two random samples of 40 students were drawn independently from two populations of students. Assume their aptitude tests are normally distributed (total points = 100). The following statistics regarding their scores in an aptitude test were obtained: 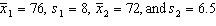 . {Aptitude Test Scores Narrative} Explain how to use the 95% confidence interval to test the hypotheses at a = .05.
. {Aptitude Test Scores Narrative} Explain how to use the 95% confidence interval to test the hypotheses at a = .05.
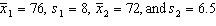 . {Aptitude Test Scores Narrative} Explain how to use the 95% confidence interval to test the hypotheses at a = .05.
. {Aptitude Test Scores Narrative} Explain how to use the 95% confidence interval to test the hypotheses at a = .05.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
79
Engine Wear To compare the wearing of two types of automobile engines, 1 and 2, an experimenter chose to "pair" the measurements, comparing the wear for the two types of engines on each of 7 automobiles, as shown below.  {Engine Wear Narrative} Estimate with 90% confidence the mean difference and interpret.
{Engine Wear Narrative} Estimate with 90% confidence the mean difference and interpret.
 {Engine Wear Narrative} Estimate with 90% confidence the mean difference and interpret.
{Engine Wear Narrative} Estimate with 90% confidence the mean difference and interpret.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
80
Additives A food processor wants to compare two additives for their effects on retarding spoilage. Suppose 16 cuts of fresh meat are treated with additive A and 16 are treated with additive B, and the number of hours until spoilage begins is recorded for each of the 32 cuts of meat. The results are summarized in the table below  {Additives Narrative} State the null and alternative hypotheses to determine if the average number of hours until spoilage begins differs for the additives A and B.
{Additives Narrative} State the null and alternative hypotheses to determine if the average number of hours until spoilage begins differs for the additives A and B.
 {Additives Narrative} State the null and alternative hypotheses to determine if the average number of hours until spoilage begins differs for the additives A and B.
{Additives Narrative} State the null and alternative hypotheses to determine if the average number of hours until spoilage begins differs for the additives A and B.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck


