Exam 12: Inference About Comparing Two Populat
Exam 1: What Is Statistics41 Questions
Exam 2: Graphical and Tabular Descriptive Techniques199 Questions
Exam 3: Numerical Descriptive Techniques226 Questions
Exam 4: Data Collection and Sampling82 Questions
Exam 5: Probability212 Questions
Exam 6: Random Variables and Discrete Probability Distributions174 Questions
Exam 7: Continuous Probability Distributions167 Questions
Exam 8: Sampling Distributions133 Questions
Exam 9: Introduction to Estimation88 Questions
Exam 10: Introduction to Hypothesis Testing186 Questions
Exam 11: Inference About a Population76 Questions
Exam 12: Inference About Comparing Two Populat85 Questions
Exam 13: Inference About Comparing Two Populat85 Questions
Exam 14: Analysis of Variance127 Questions
Exam 15: Chi-Squared Tests118 Questions
Exam 16: Simple Linear Regression and Correlat238 Questions
Exam 17: Multiple Regression147 Questions
Exam 18: Review of Statistical Inference189 Questions
Select questions type
In comparing two population means of interval data, we must decide whether the samples are independent (in which case the parameter of interest is 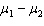 )or matched pairs (in which case the parameter is m D )in order to select the correct test statistic.
)or matched pairs (in which case the parameter is m D )in order to select the correct test statistic.
Free
(True/False)
4.8/5  (45)
(45)
Correct Answer:
True
Undergraduates' Test Scores 35 undergraduate students who completed two years of college were asked to take a basic mathematics test. The mean and standard deviation of their scores were 75.1 and 12.8, respectively. In a random sample of 50 students who only completed high school, the mean and standard deviation of the test scores were 72.1 and 14.6, respectively {Undergraduates' Test Scores Narrative} Estimate with 90% confidence the difference in mean scores between the two groups of students.
Free
(Essay)
4.8/5  (42)
(42)
Correct Answer:
3.0 ± 4.98. Thus, LCL = - 1.98, and UCL = 7.98.
Suppose we randomly selected 250 people, and on the basis of their responses to a survey we assigned them to one of two groups: high-risk group and low-risk group. We then recorded the blood pressure for the members of each group. Such data are called:
Free
(Multiple Choice)
4.8/5  (30)
(30)
Correct Answer:
A
In constructing a confidence interval estimate for the difference between the means of two independent normally distributed populations, we:
(Multiple Choice)
4.9/5  (37)
(37)
Independent samples are those for which the selection process for one is not related to the selection process for the other.
(True/False)
4.8/5  (28)
(28)
Two independent samples of sizes 25 and 35 are randomly selected from two normal populations with equal variances (assumed to be unknown). In order to test the difference between the population means, the test statistic is:
(Multiple Choice)
4.7/5  (31)
(31)
In testing the difference between two population means using two independent samples, we use the pooled variance in estimating the standard error of the sampling distribution of the sample mean difference 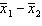 if the populations are normal with equal variances.
if the populations are normal with equal variances.
(True/False)
4.7/5  (34)
(34)
Starting Salary In testing the hypotheses 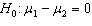 vs.
vs. 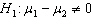 , two random samples from two populations of college of business graduates majoring in global marketing and international business produced the following statistics regarding their starting salaries (in $1000s):
, two random samples from two populations of college of business graduates majoring in global marketing and international business produced the following statistics regarding their starting salaries (in $1000s): 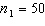 ,
, 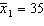 ,
, 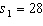 ,
, 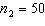 ,
, 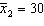 , and
, and 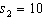 . (Assume the salaries have normal distributions.){Starting Salary Narrative} Estimate with 95% confidence the difference between the two population means.
. (Assume the salaries have normal distributions.){Starting Salary Narrative} Estimate with 95% confidence the difference between the two population means.
(Essay)
4.8/5  (26)
(26)
The sampling distribution of 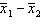 is normal if the sampled populations are normal, and approximately normal if the populations are nonnormal and the sample sizes n 1 and n 2 are large.
is normal if the sampled populations are normal, and approximately normal if the populations are nonnormal and the sample sizes n 1 and n 2 are large.
(True/False)
4.7/5  (32)
(32)
If you are testing to see if a weight loss program is working, and you subtract the weights after - before for a group of 10 people, the alternative hypothesis is that the mean difference is ____________________ 0.
(Short Answer)
4.8/5  (32)
(32)
The best estimator of the difference between two population means 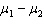 is the difference between two sample means
is the difference between two sample means 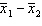 .
.
(True/False)
4.7/5  (35)
(35)
When two population variances are ____________________ we estimate each population variance with its sample variance. The test statistic of 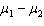 is approximately Student t -distributed with n 1 + n 2 - 2 degrees of freedom.
is approximately Student t -distributed with n 1 + n 2 - 2 degrees of freedom.
(Short Answer)
4.8/5  (27)
(27)
Two samples of sizes 25 and 20 are independently drawn from two normal populations, where the unknown population variances are assumed to be equal. The number of degrees of freedom of the equal-variances t -test statistic is 44.
(True/False)
4.7/5  (36)
(36)
The number of degrees of freedom associated with the t -test, when the data are gathered from a matched pairs experiment with 8 pairs, is 7.
(True/False)
4.9/5  (43)
(43)
If you are testing to see if a weight loss program is working, and you subtract the weights before - after for a group of 10 people, the alternative hypothesis is that the mean difference is ____________________ 0.
(Short Answer)
4.9/5  (33)
(33)
When the population variances are unequal, we estimate each population variance with its sample variance. Hence, the unequal-variances test statistic of 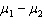 is approximately Student t -distributed with n 1 + n 2 - 2 degrees of freedom.
is approximately Student t -distributed with n 1 + n 2 - 2 degrees of freedom.
(True/False)
4.9/5  (41)
(41)
In testing the difference between the means of two normally distributed populations, the number of degrees of freedom associated with the unequal-variances t- test statistic usually results in a non-integer number. It is recommended that you:
(Multiple Choice)
4.7/5  (28)
(28)
Aptitude Test Scores Two random samples of 40 students were drawn independently from two populations of students. Assume their aptitude tests are normally distributed (total points = 100). The following statistics regarding their scores in an aptitude test were obtained: 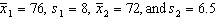 . {Aptitude Test Scores Narrative} Estimate with 95% confidence the difference between the two population means.
. {Aptitude Test Scores Narrative} Estimate with 95% confidence the difference between the two population means.
(Essay)
4.9/5  (27)
(27)
If there are 10 pairs of data in a matched pairs experiment, the degrees of freedom for the corresponding t -test is 18.
(True/False)
4.7/5  (28)
(28)
Showing 1 - 20 of 85
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)