Deck 13: Extending Understanding of Common and Decimal Fractions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/48
Play
Full screen (f)
Deck 13: Extending Understanding of Common and Decimal Fractions
1
Given the problem below, which of the following is not a correct strategy to illustrate this problem?
Juan practiced piano for ¾ hour on Tuesday, Wednesday, and Thursday. How long did he practice altogether?
A)Take 3 fraction strips 1 unit long and mark off ¾ of each strip. Lay the pieces together end to end and then separate them into halves and fourths. Add all the halves together and fourths together until all possible wholes and fractions are left.
B)Use a clock to mark off the ¾ hours, starting at 12:00 and continuing around the clock marking off ¾ portions until ending up at 2:30.
C)Using a number line, starting at 0, marking off the number line in fourths, then marking off ¾ units three times.
D)Use fraction squares, shade in ¾ on each, then adding together the pieces, forming wholes and fractional parts.
Juan practiced piano for ¾ hour on Tuesday, Wednesday, and Thursday. How long did he practice altogether?
A)Take 3 fraction strips 1 unit long and mark off ¾ of each strip. Lay the pieces together end to end and then separate them into halves and fourths. Add all the halves together and fourths together until all possible wholes and fractions are left.
B)Use a clock to mark off the ¾ hours, starting at 12:00 and continuing around the clock marking off ¾ portions until ending up at 2:30.
C)Using a number line, starting at 0, marking off the number line in fourths, then marking off ¾ units three times.
D)Use fraction squares, shade in ¾ on each, then adding together the pieces, forming wholes and fractional parts.
Use a clock to mark off the ¾ hours, starting at 12:00 and continuing around the clock marking off ¾ portions until ending up at 2:30.
2
Common fractions with denominators of factors of 2s and 5s only are known as:
A)repeating decimals.
B)terminating decimals.
C)both repeating and terminating decimals.
D)neither repeating nor terminating decimals.
A)repeating decimals.
B)terminating decimals.
C)both repeating and terminating decimals.
D)neither repeating nor terminating decimals.
terminating decimals.
3
The statements below concerning the greatest common factor (GCF)are all true except for :
A)the name for the GCF causes confusion because many times this "greatest" number can be smaller than any of the numbers under consideration.
B)the GCF is used to find the common denominator of fractions.
C)Venn diagrams can be used to illustrate the GCF of two or more numbers.
D)two numbers must have a GCF.
A)the name for the GCF causes confusion because many times this "greatest" number can be smaller than any of the numbers under consideration.
B)the GCF is used to find the common denominator of fractions.
C)Venn diagrams can be used to illustrate the GCF of two or more numbers.
D)two numbers must have a GCF.
the GCF is used to find the common denominator of fractions.
4
Which model for subtraction of common fractions is illustrated by the problem below?
Mykala bought 4¾ pounds of chicken and cooked 2½ pounds. How much chicken does she have left?
A)takeaway
B)comparison
C)completion
D)whole-part-part
Mykala bought 4¾ pounds of chicken and cooked 2½ pounds. How much chicken does she have left?
A)takeaway
B)comparison
C)completion
D)whole-part-part

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
5
Tyrone asked Mr. Jones what the answer to 0.7 × 0.3 would be. Which of the following is the best method that Mr. Jones could use to help Tyrone understand this problem conceptually?
A)Mr. Jones could tell him to count the number of decimal places to the right of each decimal, then to multiply the two numbers as if they were whole numbers, and count back that number of places from the right.
B)Mr. Jones could tell him to use base-10 pieces for each decimal, by laying down 7 longs 3 times, then to go back one decimal.
C)Mr. Jones could tell him to change each decimal into fractions, multiply out the fractions, then change back into decimals.
D)Mr. Jones could tell him to add 7 tenths three times, then to divide by one tenth.
A)Mr. Jones could tell him to count the number of decimal places to the right of each decimal, then to multiply the two numbers as if they were whole numbers, and count back that number of places from the right.
B)Mr. Jones could tell him to use base-10 pieces for each decimal, by laying down 7 longs 3 times, then to go back one decimal.
C)Mr. Jones could tell him to change each decimal into fractions, multiply out the fractions, then change back into decimals.
D)Mr. Jones could tell him to add 7 tenths three times, then to divide by one tenth.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
6
Children learn the rule "Multiplication makes bigger, division makes smaller" when working with whole numbers (with the exception of products and quotients with 0 and 1). All of the following mathematical statements concerning fractions violate this rule except for :
A)⅔ × ¾
B)⅔ × 24
C)⅔ ÷ ¾
D)1⅔ × 24
A)⅔ × ¾
B)⅔ × 24
C)⅔ ÷ ¾
D)1⅔ × 24

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
7
What is a correct expansion of 37.206?
A)(3 × 102)+ (7 × 100)+ (2 × 101)+ (6 × 103)
B)(3 × 10)+ (7 × 100)+ (2 × 1)+ (0 × 10−1)+ (6 × 10−2)
C)(3 × 101)+ (7 × 100)+ (2 × 10−1)+ (6 × 10−3)
D)(3 × 10)+ (7 × 1)+ (2 × 0.1)+ (6 × 0.01)
A)(3 × 102)+ (7 × 100)+ (2 × 101)+ (6 × 103)
B)(3 × 10)+ (7 × 100)+ (2 × 1)+ (0 × 10−1)+ (6 × 10−2)
C)(3 × 101)+ (7 × 100)+ (2 × 10−1)+ (6 × 10−3)
D)(3 × 10)+ (7 × 1)+ (2 × 0.1)+ (6 × 0.01)

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
8
The following statements below concerning the least common multiple (LCM)are all true except for:
A)The LCM is used to find the common denominator of fractions.
B)The LCM of 24, 36, and 70 is 23 × 32 × 5 × 7.
C)The LCM is used to reduce fractions down to lowest terms.
D)The LCM is confusing to children because this "least" number can be larger than any of the numbers under consideration.
A)The LCM is used to find the common denominator of fractions.
B)The LCM of 24, 36, and 70 is 23 × 32 × 5 × 7.
C)The LCM is used to reduce fractions down to lowest terms.
D)The LCM is confusing to children because this "least" number can be larger than any of the numbers under consideration.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
9
A half-gallon of milk is poured into 16 equal-sized containers. Which of the following is true with respect to this statement?
A)This is an example of the partitive model.
B)This is an example of the repeated addition model.
C)This is an example of the measurement model.
D)The correct mathematical statement for this situation is ½ × 16.
A)This is an example of the partitive model.
B)This is an example of the repeated addition model.
C)This is an example of the measurement model.
D)The correct mathematical statement for this situation is ½ × 16.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
10
Which model for subtraction of common fractions is illustrated by the problem below?
Deshawn walks 1½ miles around the track while Sam walks 1⅞ miles around the track. How much farther does Sam walk than Deshawn?
A)takeaway
B)comparison
C)completion
D)whole-part-part
Deshawn walks 1½ miles around the track while Sam walks 1⅞ miles around the track. How much farther does Sam walk than Deshawn?
A)takeaway
B)comparison
C)completion
D)whole-part-part

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
11
Research has shown that:
A)it is more difficult for students to learn rote procedures once they have acquired conceptual understanding.
B)it makes no difference for students in the long run whether conceptual practice or rote practice comes first.
C)it is more difficult for students to acquire conceptual understanding once they have learned rote procedures.
D)it is more difficult for students to acquire conceptual understanding if they simultaneously learn the comparable rote procedures.
A)it is more difficult for students to learn rote procedures once they have acquired conceptual understanding.
B)it makes no difference for students in the long run whether conceptual practice or rote practice comes first.
C)it is more difficult for students to acquire conceptual understanding once they have learned rote procedures.
D)it is more difficult for students to acquire conceptual understanding if they simultaneously learn the comparable rote procedures.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
12
A student multiplied 5½ × 3¼, but was not sure of his answer. Which of the following mathematical statements that he listed on his paper has the same meaning as the given problem?
A)(5 × 3)+ (½ × ¼)
B)(5 + ½)× 3 × ¼
C)(5 × ½)+ (3 × ¼)
D)(5 + ½)× (3 + ¼)
A)(5 × 3)+ (½ × ¼)
B)(5 + ½)× 3 × ¼
C)(5 × ½)+ (3 × ¼)
D)(5 + ½)× (3 + ¼)

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
13
The following have the value of 3.6 except for :
A)36 × 0.1
B)0.4 × 9
C)120 × 0.03
D)72 × 0.5
A)36 × 0.1
B)0.4 × 9
C)120 × 0.03
D)72 × 0.5

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
14
Which of the following situations is the correct problem for the mathematical statement 0.8 ÷ 0.2?
A)Mary has 0.8 of a yard of cloth and wants to make 2 headbands out of the cloth.
B)Jim has 0.8 of a meter of molding and needs as many 0.2 meter pieces he can cut as possible.
C)Nicole has 0.2 of a dollar and wants to increase it to 0.8 of a dollar.
D)David wants 0.2 of a 0.8 square foot piece of metal for a dog house roof.
A)Mary has 0.8 of a yard of cloth and wants to make 2 headbands out of the cloth.
B)Jim has 0.8 of a meter of molding and needs as many 0.2 meter pieces he can cut as possible.
C)Nicole has 0.2 of a dollar and wants to increase it to 0.8 of a dollar.
D)David wants 0.2 of a 0.8 square foot piece of metal for a dog house roof.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
15
Adding fractions should be introduced in which order (from least to most complex)?
A)like denominators, unlike denominators, one denominator that is a multiple of another
B)unlike denominators, one denominator that is a multiple of another, like denominators
C)like denominators, one denominator that is a multiple of another, unlike denominators
D)unlike denominators, like denominators, one denominator that is a multiple of another
A)like denominators, unlike denominators, one denominator that is a multiple of another
B)unlike denominators, one denominator that is a multiple of another, like denominators
C)like denominators, one denominator that is a multiple of another, unlike denominators
D)unlike denominators, like denominators, one denominator that is a multiple of another

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
16
Which model for subtraction of common fractions is illustrated by the problem below?
Emily has ⅝ cup of flour but needs 1¼ cups to make bread. How much more flour does she need?
A)takeaway
B)comparison
C)completion
D)whole-part-part
Emily has ⅝ cup of flour but needs 1¼ cups to make bread. How much more flour does she need?
A)takeaway
B)comparison
C)completion
D)whole-part-part

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
17
The density property refers to:
A)the thickness of the width of a number line.
B)the property that states that there is always another number between any two numbers.
C)the necessity for students to recognize how dense the curriculum is when learning about fractions.
D)the equivalency of fractions to decimals.
A)the thickness of the width of a number line.
B)the property that states that there is always another number between any two numbers.
C)the necessity for students to recognize how dense the curriculum is when learning about fractions.
D)the equivalency of fractions to decimals.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
18
John wants to get ⅔ of his money out of the bank, but he has to pay his brother ⅙ of that. Which of the following statements shows what John would have left of the amount he took out of the bank, after paying his brother?
A)⅔ - ⅙
B)⅔ × ⅙
C)1 - (⅔ × ⅙)
D)⅔ × ⅚
A)⅔ - ⅙
B)⅔ × ⅙
C)1 - (⅔ × ⅙)
D)⅔ × ⅚

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
19
"Lining up the decimal points" is the rote rule that children learn when adding and subtracting decimal fractions. The reasoning behind this rule is:
A)children are following the "one place value at a time" rule when adding and subtracting, similar to what they followed with whole numbers.
B)children will not add together or subtract the wrong numbers.
C)that base-10 blocks won't be necessary for conceptual understanding in this case.
D)that real-life examples won't be necessary for conceptual understanding in this case.
A)children are following the "one place value at a time" rule when adding and subtracting, similar to what they followed with whole numbers.
B)children will not add together or subtract the wrong numbers.
C)that base-10 blocks won't be necessary for conceptual understanding in this case.
D)that real-life examples won't be necessary for conceptual understanding in this case.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
20
The correct sequence when adding fractions is:
A)working with fractions with like denominators, then mixed numerals with unlike denominators, then fractions with like denominators.
B)working with fractions with unlike denominators, then working with fractions with like denominators, then working with mixed numerals.
C)working with fractions with unlike denominators, then working with mixed numerals with like denominators, then working with fractions with like denominators.
D)working with fractions with like denominators, then fractions with unlike denominators, then working with mixed numerals.
A)working with fractions with like denominators, then mixed numerals with unlike denominators, then fractions with like denominators.
B)working with fractions with unlike denominators, then working with fractions with like denominators, then working with mixed numerals.
C)working with fractions with unlike denominators, then working with mixed numerals with like denominators, then working with fractions with like denominators.
D)working with fractions with like denominators, then fractions with unlike denominators, then working with mixed numerals.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
21
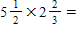
A)
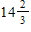
B)
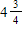
C)
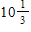
D)
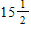

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
22
Some teachers say that using manipulatives for teaching fractions just confuses children and that they do just fine learning the traditional algorithms. Do you agree or disagree with these statements? Why or why not?

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
23
How could you convince children that they need to have common denominators when adding and subtracting common fractions?

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
24
Which of these fractions is a terminating decimal?
A)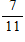
B)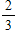
C)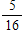
D)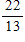
A)
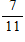
B)
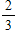
C)
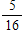
D)
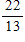

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
25
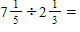
A)
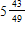
B)
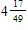
C)
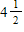
D)
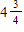

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
26
Everett found out that the exchange rate between Singapore dollars and South African rand was:
1 SGD = 4.2 ZAR
Everett changed 3,000 Singapore dollars into South African rand at this exchange rate. How much money in South African rand did Everett get?
1 SGD = 4.2 ZAR
Everett changed 3,000 Singapore dollars into South African rand at this exchange rate. How much money in South African rand did Everett get?

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
27
4.8 ÷ 0.2 =
A)0.24
B)240
C)24
D)2.4
A)0.24
B)240
C)24
D)2.4

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
28
9.6 × 4.23 =
A)40.68
B)4.068
C)406.8
D)4068.0
A)40.68
B)4.068
C)406.8
D)4068.0

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
29
What is the progression you should use to teach children to add and subtract fractions? Use examples to illustrate the progression.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
30
Why is the expansion of decimals important for upper elementary children?

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
31
Mason is 50 inches tall and is growing at the rate of 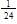
inch per month. Owen is 47 inches tall and is growing at the rate of
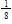
Inch per month. If they continue to grow at these rates for the next four years, in how many months will they be the same height?
A)24 months
B)30 months
C)36 months
D)42 months
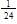
inch per month. Owen is 47 inches tall and is growing at the rate of
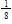
Inch per month. If they continue to grow at these rates for the next four years, in how many months will they be the same height?
A)24 months
B)30 months
C)36 months
D)42 months

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
32
How could you explain the density property to children?

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
33
Explain how you would help children make the transition between common fractions and decimal fractions.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
34
12 - 8.34 =
A)4.66
B)3.66
C)4.34
D)6.34
A)4.66
B)3.66
C)4.34
D)6.34

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
35
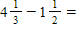
A)
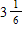
B)
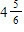
C)
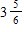
D)
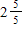

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
36
What is the least common multiple (LCM)for 36 and 48?
A)288
B)144
C)192
D)576
A)288
B)144
C)192
D)576

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
37
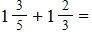
A)
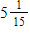
B)
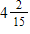
C)
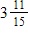
D)
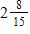

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
38
In which of these pairs of numbers is 2.25 larger than the first number but smaller than the second number?
A)1 and 2
B)2 and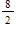
C)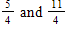
D)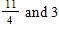
A)1 and 2
B)2 and
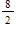
C)
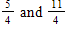
D)

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
39
On the number line given here, what number would be located at point P?



Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
40
4.5 + 6.23 + 8.25 + 6 =
A)19.58
B)20.58
C)21.98
D)24.98
A)19.58
B)20.58
C)21.98
D)24.98

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
41
Sketch models to convince children that the expressions below are equal to their correct answers.
(a)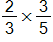
(b)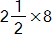
(c)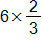
(d)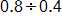
What is the value in making sketches such as these?
(a)
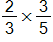
(b)
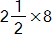
(c)
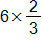
(d)
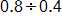
What is the value in making sketches such as these?

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
42
Explain how GCFs and LCMs are related to common fractions.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
43
A student solved
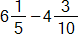
by subtracting 6 - 4 to obtain 2 and
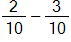
to obtain
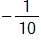
. She then subtracted
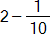
to get
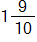
. Is this a legitimate algorithm? Will it always work? Explain why or why not.
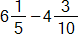
by subtracting 6 - 4 to obtain 2 and
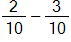
to obtain
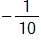
. She then subtracted
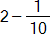
to get
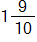
. Is this a legitimate algorithm? Will it always work? Explain why or why not.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
44
Use pattern blocks to make a design in which ⅓ is made of trapezoids. Trace your design. Shade the trapezoids.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
45
Performance Task: Using Pattern Blocks and Tangrams
Use pattern blocks or tangrams to complete each performance task.
Use pattern blocks to make a design in which 1¼ is green. Trace your design. Shade the green part.
Use pattern blocks or tangrams to complete each performance task.
Use pattern blocks to make a design in which 1¼ is green. Trace your design. Shade the green part.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
46
Give several examples of how calculators can be beneficial when teaching common fractions and decimal fractions.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
47
Illustrate and describe how tangrams can be used to develop the concepts of ½ and ¼ .

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
48
Represent ⅓ and ⅔ using pattern blocks.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck


