Exam 13: Extending Understanding of Common and Decimal Fractions
What is the least common multiple (LCM)for 36 and 48?
B
The following statements below concerning the least common multiple (LCM)are all true except for:
C
Explain how you would help children make the transition between common fractions and decimal fractions.
To help children make the transition between common fractions and decimal fractions, I would use a variety of hands-on and visual aids to demonstrate the relationship between the two.
First, I would start by using visual representations such as fraction bars or circles to show how a fraction can be represented as a decimal. For example, I would show that 1/2 is the same as 0.5, and 1/4 is the same as 0.25. This visual representation helps children see the connection between the two forms.
Next, I would provide plenty of practice problems that require converting between fractions and decimals. This could include simple exercises like converting 1/4 to a decimal, or more complex problems like converting 3/5 to a decimal. By practicing these conversions, children can become more comfortable with the process and develop a deeper understanding of the relationship between fractions and decimals.
I would also use real-life examples to show how decimals are used in everyday situations. For example, I might show how prices at the grocery store are often listed in decimal form, or how measurements such as 1.5 meters are used in construction. By connecting decimals to real-world applications, children can see the practical value of understanding and being able to convert between fractions and decimals.
Overall, by using visual aids, providing plenty of practice, and connecting decimals to real-life examples, I would help children make a smooth transition between common fractions and decimal fractions.
John wants to get ⅔ of his money out of the bank, but he has to pay his brother ⅙ of that. Which of the following statements shows what John would have left of the amount he took out of the bank, after paying his brother?
"Lining up the decimal points" is the rote rule that children learn when adding and subtracting decimal fractions. The reasoning behind this rule is:
A student solved
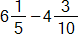 by subtracting 6 - 4 to obtain 2 and
by subtracting 6 - 4 to obtain 2 and
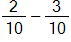 to obtain
to obtain
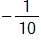 . She then subtracted
. She then subtracted
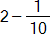 to get
to get
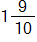 . Is this a legitimate algorithm? Will it always work? Explain why or why not.
. Is this a legitimate algorithm? Will it always work? Explain why or why not.
A half-gallon of milk is poured into 16 equal-sized containers. Which of the following is true with respect to this statement?
Common fractions with denominators of factors of 2s and 5s only are known as:
Given the problem below, which of the following is not a correct strategy to illustrate this problem?
Juan practiced piano for ¾ hour on Tuesday, Wednesday, and Thursday. How long did he practice altogether?
A student multiplied 5½ × 3¼, but was not sure of his answer. Which of the following mathematical statements that he listed on his paper has the same meaning as the given problem?
Everett found out that the exchange rate between Singapore dollars and South African rand was:
1 SGD = 4.2 ZAR
Everett changed 3,000 Singapore dollars into South African rand at this exchange rate. How much money in South African rand did Everett get?
Tyrone asked Mr. Jones what the answer to 0.7 × 0.3 would be. Which of the following is the best method that Mr. Jones could use to help Tyrone understand this problem conceptually?
Illustrate and describe how tangrams can be used to develop the concepts of ½ and ¼ .
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)