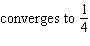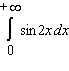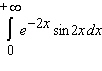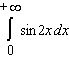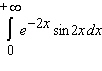Deck 9: Trigonometric Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Match between columns
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/66
Play
Full screen (f)
Deck 9: Trigonometric Models
1
Use the formula for 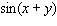 to simplify the expression
to simplify the expression 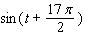 .
.
A)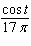
B)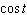
C)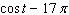
D)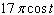
E)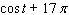
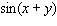 to simplify the expression
to simplify the expression 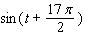 .
.A)
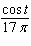
B)
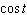
C)
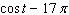
D)
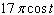
E)
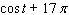
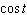
2
Sales of computers are subject to seasonal fluctuations. Computer City s sales of computers in 1995 and 1996 can be approximated by the function 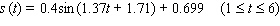 where t is time in quarters ( t = 1 represents the end of the first quarter of 1995 )and s ( t )is computer sales ( quarterly revenue )in billions of dollars. Estimate Computer City s maximum and minimum quarterly revenue from computer sales.
where t is time in quarters ( t = 1 represents the end of the first quarter of 1995 )and s ( t )is computer sales ( quarterly revenue )in billions of dollars. Estimate Computer City s maximum and minimum quarterly revenue from computer sales.
A)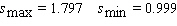
B)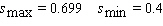
C)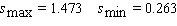
D)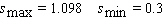
E)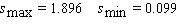
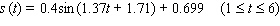 where t is time in quarters ( t = 1 represents the end of the first quarter of 1995 )and s ( t )is computer sales ( quarterly revenue )in billions of dollars. Estimate Computer City s maximum and minimum quarterly revenue from computer sales.
where t is time in quarters ( t = 1 represents the end of the first quarter of 1995 )and s ( t )is computer sales ( quarterly revenue )in billions of dollars. Estimate Computer City s maximum and minimum quarterly revenue from computer sales.A)
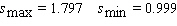
B)
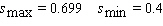
C)
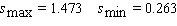
D)
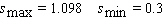
E)
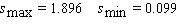
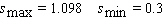
3
The depth of water  at my favorite surfing spot varies from 9 to 20 feet, depending on the time. Last Sunday high tide occurred at 5:00 A.M. and the next high tide occurred at 6:30 P.M. Use a sine function to model the depth of water as a function of time t in hours since midnight on Sunday morning.
at my favorite surfing spot varies from 9 to 20 feet, depending on the time. Last Sunday high tide occurred at 5:00 A.M. and the next high tide occurred at 6:30 P.M. Use a sine function to model the depth of water as a function of time t in hours since midnight on Sunday morning.
A)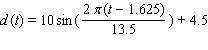
B)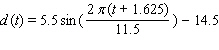
C)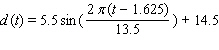
D)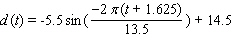
E)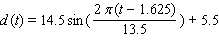
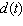 at my favorite surfing spot varies from 9 to 20 feet, depending on the time. Last Sunday high tide occurred at 5:00 A.M. and the next high tide occurred at 6:30 P.M. Use a sine function to model the depth of water as a function of time t in hours since midnight on Sunday morning.
at my favorite surfing spot varies from 9 to 20 feet, depending on the time. Last Sunday high tide occurred at 5:00 A.M. and the next high tide occurred at 6:30 P.M. Use a sine function to model the depth of water as a function of time t in hours since midnight on Sunday morning.A)
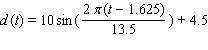
B)
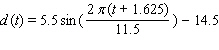
C)
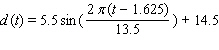
D)
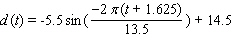
E)
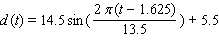
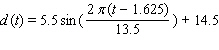
4
Use the addition formulas: sin ( x + y )= sin x cos y + cos x sin y sin ( x - y )= sin x cos y - cos x sin y cos ( x + y )= cos x cos y - sin x sin y cos ( x - y )= cos x cos y + sin x sin y to express 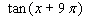 in terms of
in terms of 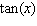 .
.
A)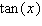
B)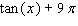
C)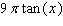
D)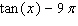
E)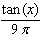
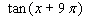 in terms of
in terms of 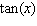 .
.A)
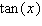
B)
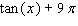
C)
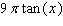
D)
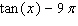
E)
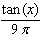

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
5
Model the curve with a cosine function. 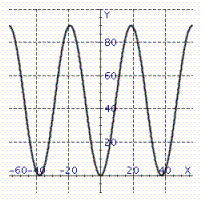 Note that the period of the curve is
Note that the period of the curve is 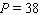 , its range is
, its range is 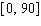 the graph of the cosine function is shifted upward 45 units and shifted to the right 19 units.
the graph of the cosine function is shifted upward 45 units and shifted to the right 19 units.
A)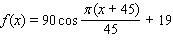
B)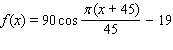
C)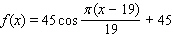
D)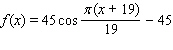
E)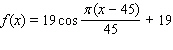
 Note that the period of the curve is
Note that the period of the curve is 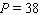 , its range is
, its range is 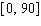 the graph of the cosine function is shifted upward 45 units and shifted to the right 19 units.
the graph of the cosine function is shifted upward 45 units and shifted to the right 19 units.A)
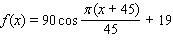
B)
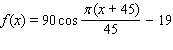
C)
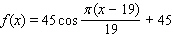
D)
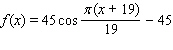
E)
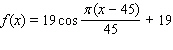

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
6
Starting with the identity 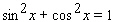 , choose the right trigonometric identity.
, choose the right trigonometric identity.
A)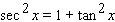
B)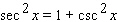
C)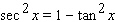
D)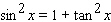
E)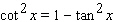
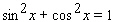 , choose the right trigonometric identity.
, choose the right trigonometric identity.A)
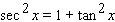
B)
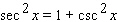
C)
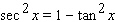
D)
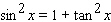
E)
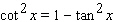

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
7
Use the conversion formula 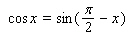 to replace the expression
to replace the expression 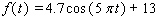 by a sine function.
by a sine function.
A)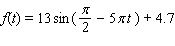
B)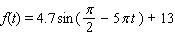
C)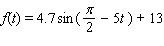
D)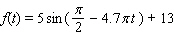
E)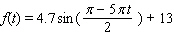
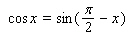 to replace the expression
to replace the expression 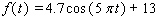 by a sine function.
by a sine function.A)
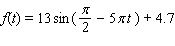
B)
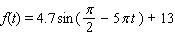
C)
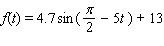
D)
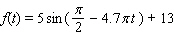
E)
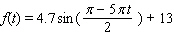

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
8
Sketch the curves without any technological help. 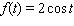 ;
; 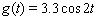
A)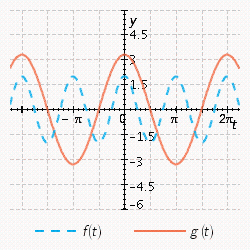
B)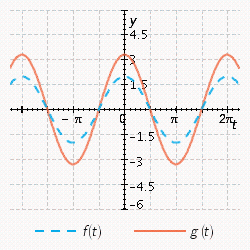
C)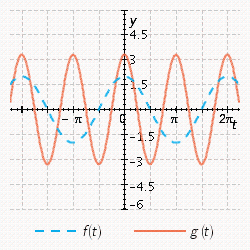
D)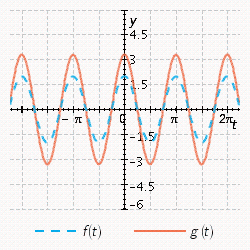
E)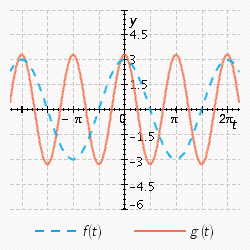
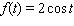 ;
; 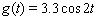
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
9
Model the curve with a sine function. 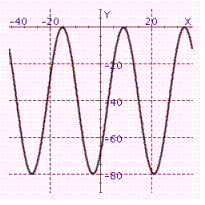 Note that the period of the curve is
Note that the period of the curve is 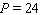 and its range is
and its range is 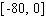 , the graph of the sine function is shifted to the right 3 units.
, the graph of the sine function is shifted to the right 3 units.
A)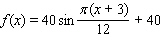
B)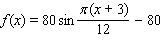
C)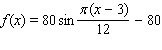
D)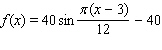
E)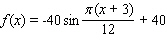
 Note that the period of the curve is
Note that the period of the curve is 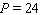 and its range is
and its range is 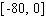 , the graph of the sine function is shifted to the right 3 units.
, the graph of the sine function is shifted to the right 3 units.A)
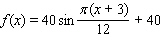
B)
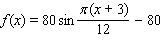
C)
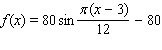
D)
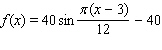
E)
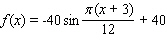

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
10
The uninflated cost of Dugout brand snow shovels currently varies from a high of $22 on January 1 ( t = 0 )to a low of $8 on July 1 ( t = 0.5). Assuming this trend were to continue indefinitely, calculate the uninflated cost 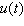 of Dugout snow shovels as a function of time t in years. (Use a sine function.)
of Dugout snow shovels as a function of time t in years. (Use a sine function.)
A)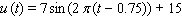
B)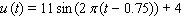
C)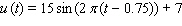
D)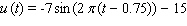
E)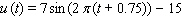
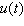 of Dugout snow shovels as a function of time t in years. (Use a sine function.)
of Dugout snow shovels as a function of time t in years. (Use a sine function.)A)
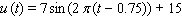
B)
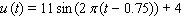
C)
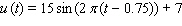
D)
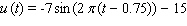
E)
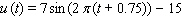

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
11
Sketch the curves without any technological help. 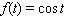 ;
; 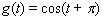
A)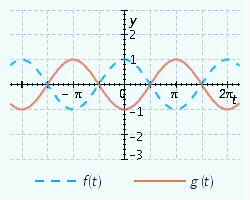
B)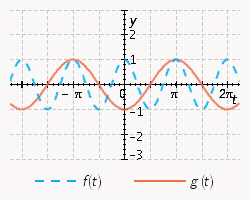
C)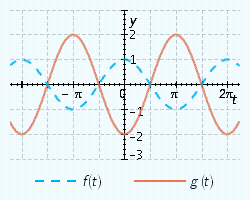
D)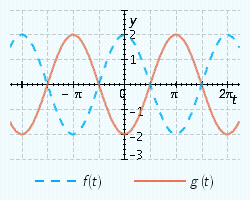
E)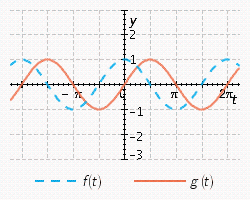
 ;
; 
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
12
Model the curve with a cosine function. 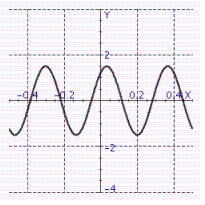 Note that the period of the curve is
Note that the period of the curve is 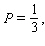 its range is
its range is 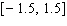 and the graph of the cosine function is shifted to the right 0.7 units.
and the graph of the cosine function is shifted to the right 0.7 units.
A)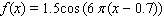
B)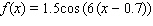
C)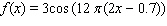
D)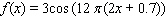
E)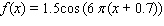
 Note that the period of the curve is
Note that the period of the curve is 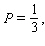 its range is
its range is 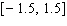 and the graph of the cosine function is shifted to the right 0.7 units.
and the graph of the cosine function is shifted to the right 0.7 units.A)
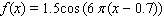
B)
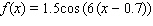
C)
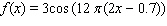
D)
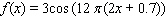
E)
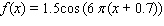

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
13
Model the curve with a sine function. 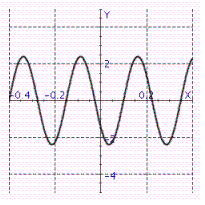 Note that the period of the curve is
Note that the period of the curve is 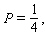 its range is 2.4, 2.4 and the graph of the sine function is shifted to the left 0.9 units. Write the model function as a function of (x)and
its range is 2.4, 2.4 and the graph of the sine function is shifted to the left 0.9 units. Write the model function as a function of (x)and 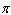 .
.
 Note that the period of the curve is
Note that the period of the curve is 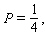 its range is 2.4, 2.4 and the graph of the sine function is shifted to the left 0.9 units. Write the model function as a function of (x)and
its range is 2.4, 2.4 and the graph of the sine function is shifted to the left 0.9 units. Write the model function as a function of (x)and 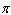 .
.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
14
Use the conversion formula 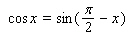 to replace the expression
to replace the expression 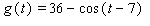 by a sine function.
by a sine function.
A)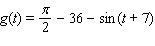
B)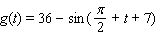
C)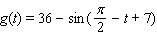
D)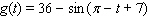
E)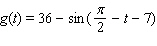
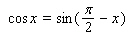 to replace the expression
to replace the expression 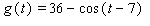 by a sine function.
by a sine function.A)
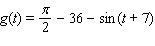
B)
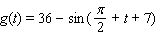
C)
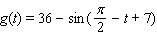
D)
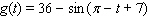
E)
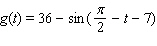

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
15
Model the curve with a sine function. 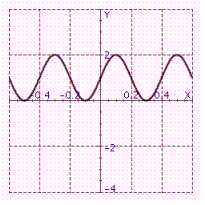 Note that the period of the curve is
Note that the period of the curve is 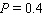 and its range is
and its range is 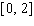 .
.
A)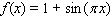
B)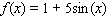
C)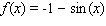
D)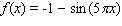
E)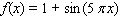
 Note that the period of the curve is
Note that the period of the curve is 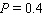 and its range is
and its range is 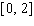 .
.A)
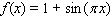
B)
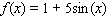
C)
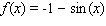
D)
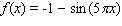
E)
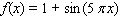

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
16
Model the curve with a cosine function. 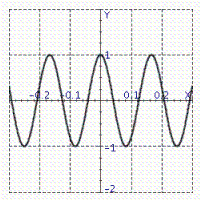 Note that the period of the curve is
Note that the period of the curve is 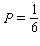 and its range is
and its range is 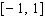 .
.
A)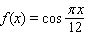
B)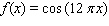
C)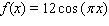
D)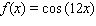
E)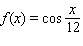
 Note that the period of the curve is
Note that the period of the curve is 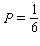 and its range is
and its range is 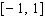 .
.A)
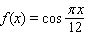
B)
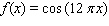
C)
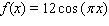
D)
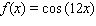
E)
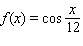

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
17
Model the curve with a sine function. 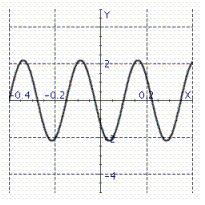 Note that the period of the curve is
Note that the period of the curve is 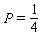 and its range is 2.2, 2.2 and the graph of the sine function is shifted to the left 0.9 units.
and its range is 2.2, 2.2 and the graph of the sine function is shifted to the left 0.9 units.
A)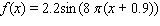
B)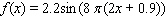
C)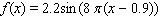
D)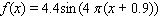
E)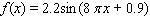
 Note that the period of the curve is
Note that the period of the curve is 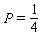 and its range is 2.2, 2.2 and the graph of the sine function is shifted to the left 0.9 units.
and its range is 2.2, 2.2 and the graph of the sine function is shifted to the left 0.9 units.A)
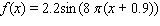
B)
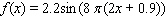
C)
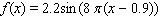
D)
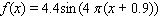
E)
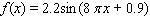

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
18
Use the conversion formula 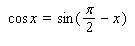 to replace the expression
to replace the expression 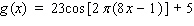 by a sine function.
by a sine function.
A)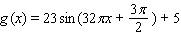
B)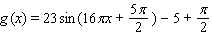
C)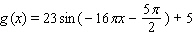
D)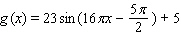
E)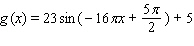
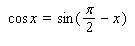 to replace the expression
to replace the expression 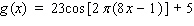 by a sine function.
by a sine function.A)
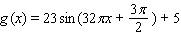
B)
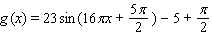
C)
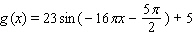
D)
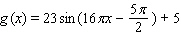
E)
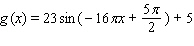

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
19
Model the curve with a cosine function. 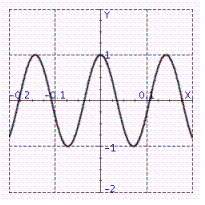 Note that the period of the curve is
Note that the period of the curve is 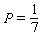 and its range is
and its range is 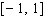 .
.
A)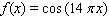
B)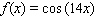
C)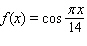
D)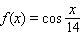
E)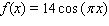
 Note that the period of the curve is
Note that the period of the curve is 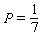 and its range is
and its range is 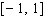 .
.A)
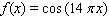
B)
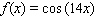
C)
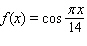
D)
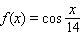
E)
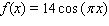

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
20
Use the addition formulas : 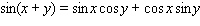
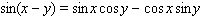
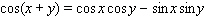
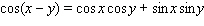 to calculate
to calculate 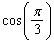 , given that
, given that 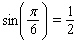 and
and 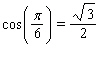 .
.
A)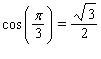
B)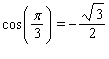
C)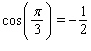
D)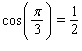
E)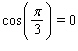
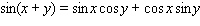
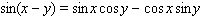
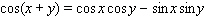
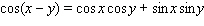 to calculate
to calculate 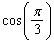 , given that
, given that 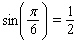 and
and 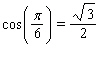 .
.A)
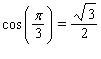
B)
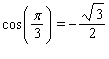
C)
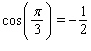
D)
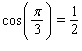
E)
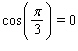

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
21
Find the derivative of the function. 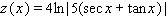
A)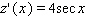
B)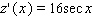
C)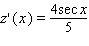
D)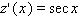
E)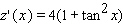
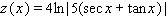
A)
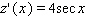
B)
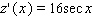
C)
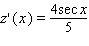
D)
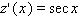
E)
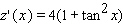

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
22
Find the derivative of the function. 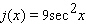
A)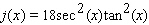
B)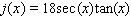
C)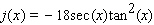
D)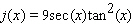
E)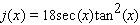
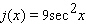
A)
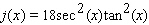
B)
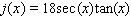
C)
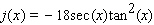
D)
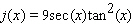
E)
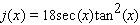

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
23
Find the derivative of the function. 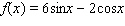
A)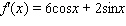
B)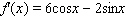
C)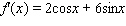
D)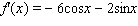
E)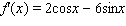
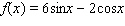
A)
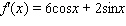
B)
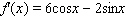
C)
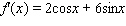
D)
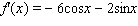
E)
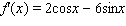

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
24
Starting with the identity 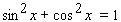 and then dividing both sides of the equation by a suitable trigonometric function, derive the trigonometric identity.
and then dividing both sides of the equation by a suitable trigonometric function, derive the trigonometric identity. 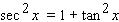
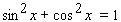 and then dividing both sides of the equation by a suitable trigonometric function, derive the trigonometric identity.
and then dividing both sides of the equation by a suitable trigonometric function, derive the trigonometric identity. 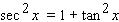

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
25
Find the derivative of the function. 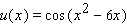
A)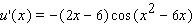
B)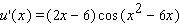
C)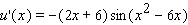
D)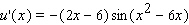
E)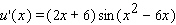
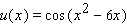
A)
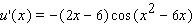
B)
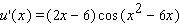
C)
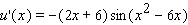
D)
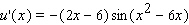
E)
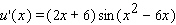

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
26
Find the derivative of the function. 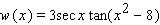
A)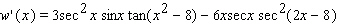
B)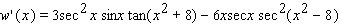
C)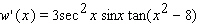
D)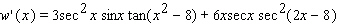
E)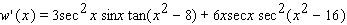
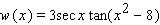
A)
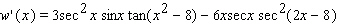
B)
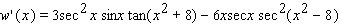
C)
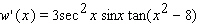
D)
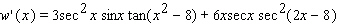
E)
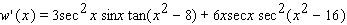

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
27
Find the derivative of the function. 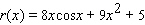
A)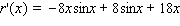
B)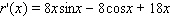
C)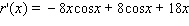
D)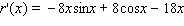
E)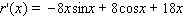
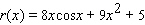
A)
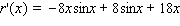
B)
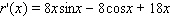
C)
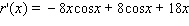
D)
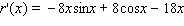
E)
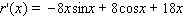

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
28
Calculate the derivative. 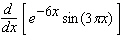
A)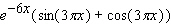
B)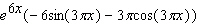
C)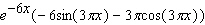
D)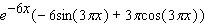
E)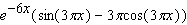
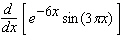
A)
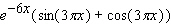
B)
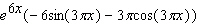
C)
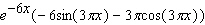
D)
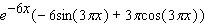
E)
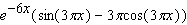

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
29
Sales of computers are subject to seasonal fluctuations. Computer City s sales of computers in 1995 and 1996 can be approximated by the function 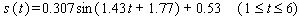 where
where 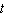 is time in quarters
is time in quarters 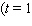 represents the end of the first quarter of 1995)and
represents the end of the first quarter of 1995)and 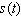 is computer sales (quarterly revenue)in billions of dollars. Estimate Computer City s maximum and minimum quarterly revenue from computer sales. Maximum sales __________ billions of dollars Minimum sales __________ billions of dollars
is computer sales (quarterly revenue)in billions of dollars. Estimate Computer City s maximum and minimum quarterly revenue from computer sales. Maximum sales __________ billions of dollars Minimum sales __________ billions of dollars
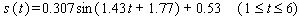 where
where 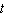 is time in quarters
is time in quarters 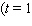 represents the end of the first quarter of 1995)and
represents the end of the first quarter of 1995)and 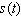 is computer sales (quarterly revenue)in billions of dollars. Estimate Computer City s maximum and minimum quarterly revenue from computer sales. Maximum sales __________ billions of dollars Minimum sales __________ billions of dollars
is computer sales (quarterly revenue)in billions of dollars. Estimate Computer City s maximum and minimum quarterly revenue from computer sales. Maximum sales __________ billions of dollars Minimum sales __________ billions of dollars
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
30
Find the derivative of the function. 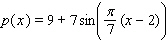
A)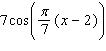
B)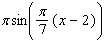
C)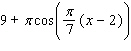
D)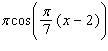
E)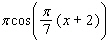
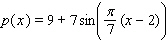
A)
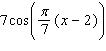
B)
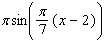
C)
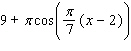
D)
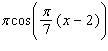
E)
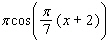

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
31
Find the derivative of the function. 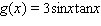
A)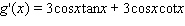
B)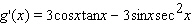
C)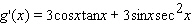
D)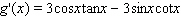
E)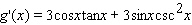
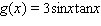
A)
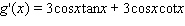
B)
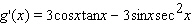
C)
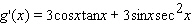
D)
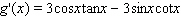
E)
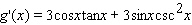

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
32
Find the derivative of the function. 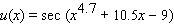
A)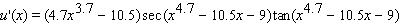
B)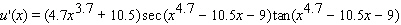
C)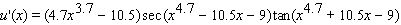
D)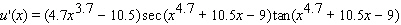
E)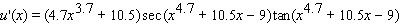
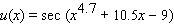
A)
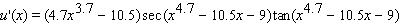
B)
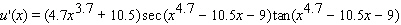
C)
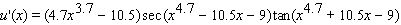
D)
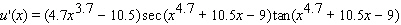
E)
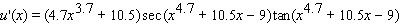

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
33
Model the curve with a cosine function. 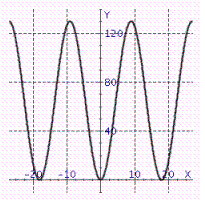 Note that the period of the curve is
Note that the period of the curve is 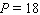 , its range is
, its range is 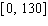 and the graph of the cosine function is shifted upward 65 units and shifted to the right 9 units. Write the model function as a function of (x)and
and the graph of the cosine function is shifted upward 65 units and shifted to the right 9 units. Write the model function as a function of (x)and 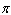 .
.
 Note that the period of the curve is
Note that the period of the curve is 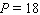 , its range is
, its range is 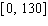 and the graph of the cosine function is shifted upward 65 units and shifted to the right 9 units. Write the model function as a function of (x)and
and the graph of the cosine function is shifted upward 65 units and shifted to the right 9 units. Write the model function as a function of (x)and 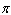 .
.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
34
Find the derivative of the function. 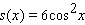
A)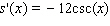
B)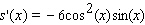
C)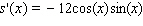
D)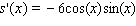
E)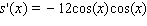
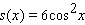
A)
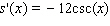
B)
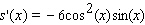
C)
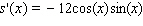
D)
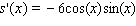
E)
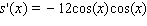

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
35
Model the curve with a sine function. 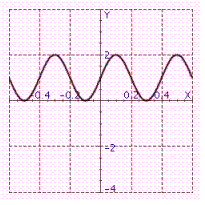 Note that the period of the curve is
Note that the period of the curve is 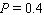 and its range is
and its range is 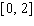 . Write the model function as a function of (x)and
. Write the model function as a function of (x)and 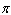 .
.
 Note that the period of the curve is
Note that the period of the curve is 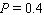 and its range is
and its range is 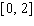 . Write the model function as a function of (x)and
. Write the model function as a function of (x)and 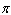 .
.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
36
Find the derivative of the function. 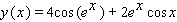
A)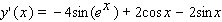
B)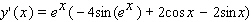
C)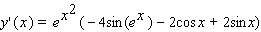
D)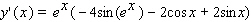
E)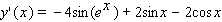
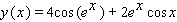
A)
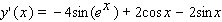
B)
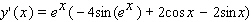
C)
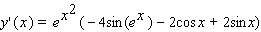
D)
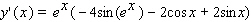
E)
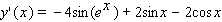

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
37
Find the derivative of the function. 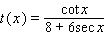
A)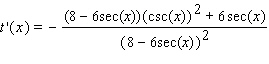
B)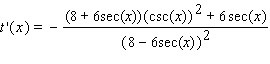
C)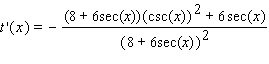
D)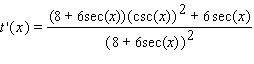
E)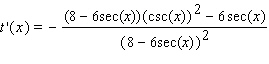
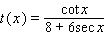
A)
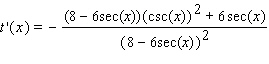
B)
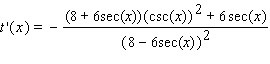
C)
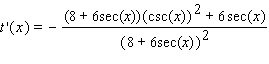
D)
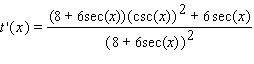
E)
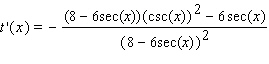

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
38
Find the derivative of the function. 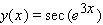
A)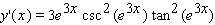
B)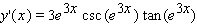
C)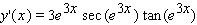
D)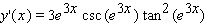
E)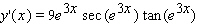
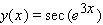
A)
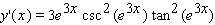
B)
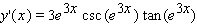
C)
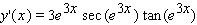
D)
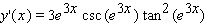
E)
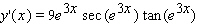

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
39
Find the derivative of the function. 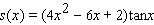
A)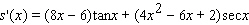
B)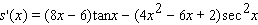
C)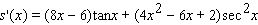
D)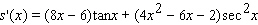
E)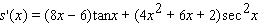
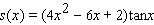
A)
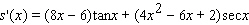
B)
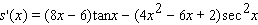
C)
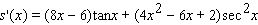
D)
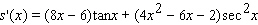
E)
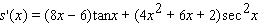

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
40
The depth of water 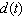 at my favorite surfing spot varies from 5 to 15 feet, depending on the time. Last Sunday high tide occurred at 5:00 A.M. and the next high tide occurred at 6:30 P.M. Use a sine function to model to the depth of water as a function of time t in hours since midnight in Sunday morning.
at my favorite surfing spot varies from 5 to 15 feet, depending on the time. Last Sunday high tide occurred at 5:00 A.M. and the next high tide occurred at 6:30 P.M. Use a sine function to model to the depth of water as a function of time t in hours since midnight in Sunday morning.
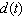 at my favorite surfing spot varies from 5 to 15 feet, depending on the time. Last Sunday high tide occurred at 5:00 A.M. and the next high tide occurred at 6:30 P.M. Use a sine function to model to the depth of water as a function of time t in hours since midnight in Sunday morning.
at my favorite surfing spot varies from 5 to 15 feet, depending on the time. Last Sunday high tide occurred at 5:00 A.M. and the next high tide occurred at 6:30 P.M. Use a sine function to model to the depth of water as a function of time t in hours since midnight in Sunday morning.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
41
Evaluate the integral. 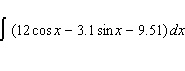
A)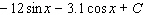
B)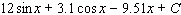
C)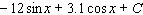
D)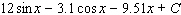
E)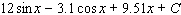
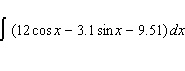
A)
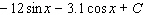
B)
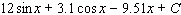
C)
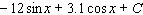
D)
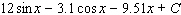
E)
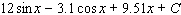

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
42
Evaluate the integral. 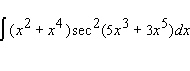
A)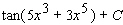
B)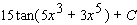
C)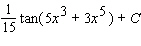
D)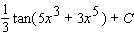
E)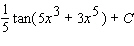
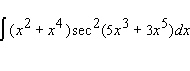
A)
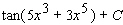
B)
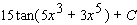
C)
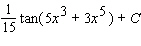
D)
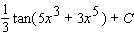
E)
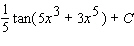

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
43
Evaluate the integral. 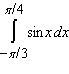
A)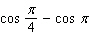
B)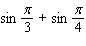
C)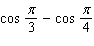
D)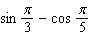
E)none of these
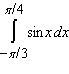
A)
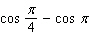
B)
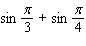
C)
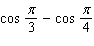
D)
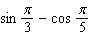
E)none of these

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
44
Recall that the average of a function 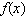 on an interval
on an interval 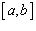 is
is 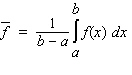 Calculate the 2-unit moving average of the function.
Calculate the 2-unit moving average of the function. 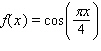
A)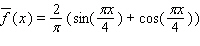
B)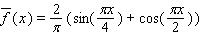
C)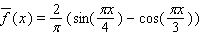
D)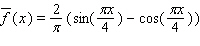
E)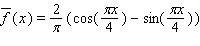
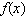 on an interval
on an interval 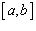 is
is 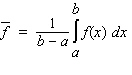 Calculate the 2-unit moving average of the function.
Calculate the 2-unit moving average of the function. 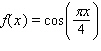
A)
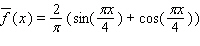
B)
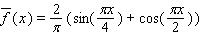
C)
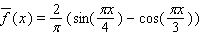
D)
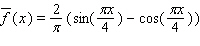
E)
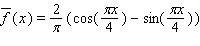

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
45
The cost of Dig-It brand snow shovels is given by 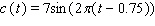 where t is time in years since January 1, 1997. How fast, in dollars per year, is the cost increasing on October 30, 1997?
where t is time in years since January 1, 1997. How fast, in dollars per year, is the cost increasing on October 30, 1997?
A)$21.99 per year
B)$14 per year
C)$45.98 per year
D)$46.98 per year
E)$43.98 per year
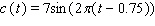 where t is time in years since January 1, 1997. How fast, in dollars per year, is the cost increasing on October 30, 1997?
where t is time in years since January 1, 1997. How fast, in dollars per year, is the cost increasing on October 30, 1997?A)$21.99 per year
B)$14 per year
C)$45.98 per year
D)$46.98 per year
E)$43.98 per year

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
46
Recall that the average of a function 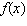 on an interval
on an interval 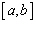 is
is 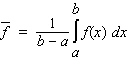 Find the average of the given function.
Find the average of the given function. 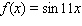 over
over 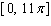 .
.
A)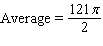
B)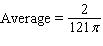
C)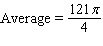
D)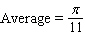
E)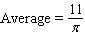
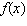 on an interval
on an interval 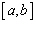 is
is 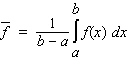 Find the average of the given function.
Find the average of the given function. 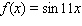 over
over 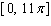 .
.A)
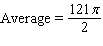
B)
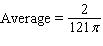
C)
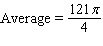
D)
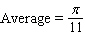
E)
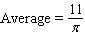

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
47
Use geometry to compute the given integral. 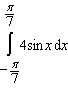
A)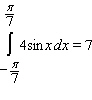
B)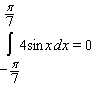
C)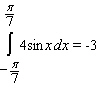
D)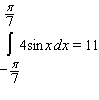
E)none of these
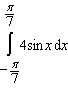
A)
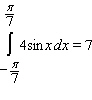
B)
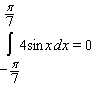
C)
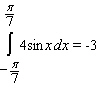
D)
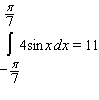
E)none of these

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
48
Use geometry to compute the given integral. 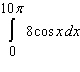
A)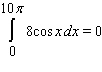
B)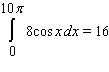
C)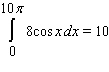
D)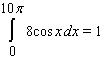
E)none of these
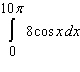
A)
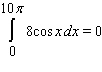
B)
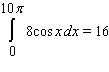
C)
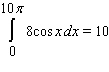
D)
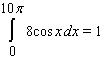
E)none of these

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
49
Evaluate the integral. 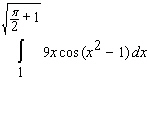
A)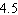
B)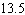
C)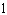
D)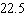
E)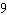
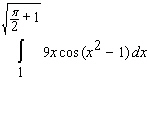
A)
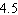
B)
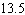
C)
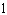
D)
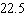
E)
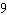

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
50
Calculate the derivative. 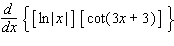
A)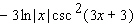
B)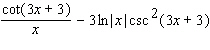
C)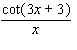
D)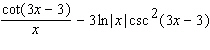
E)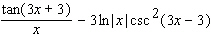
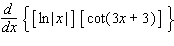
A)
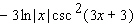
B)
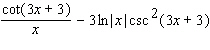
C)
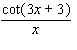
D)
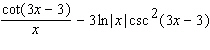
E)
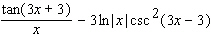

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
51
Evaluate the integral 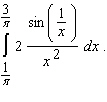
A)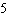
B)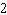
C)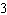
D)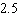
E)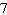
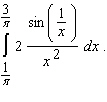
A)
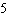
B)
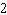
C)
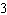
D)
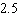
E)
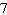

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
52
Evaluate the integral. 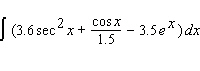
A)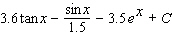
B)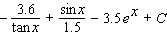
C)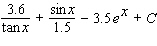
D)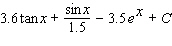
E)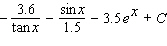
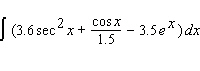
A)
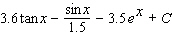
B)
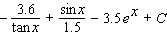
C)
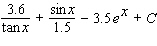
D)
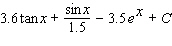
E)
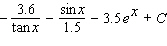

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
53
Calculate the derivative. 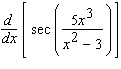
A)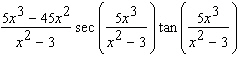
B)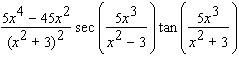
C)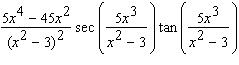
D)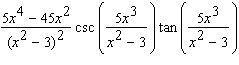
E)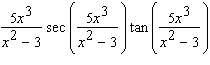
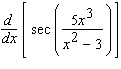
A)
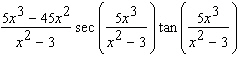
B)
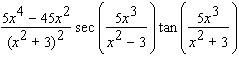
C)
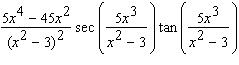
D)
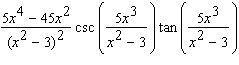
E)
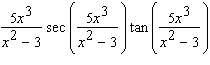

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
54
Evaluate the integral. 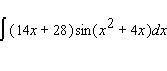
A)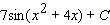
B)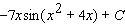
C)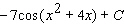
D)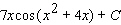
E)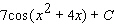
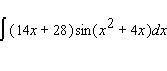
A)
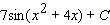
B)
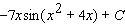
C)
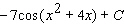
D)
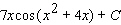
E)
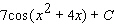

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
55
Calculate the derivative. 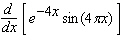
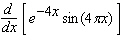

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
56
Calculate the derivative. 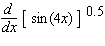
A)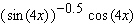
B)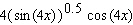
C)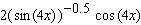
D)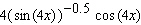
E)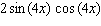
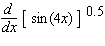
A)
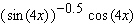
B)
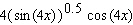
C)
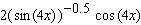
D)
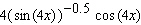
E)
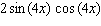

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
57
Evaluate the integral. 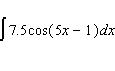
A)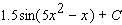
B)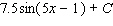
C)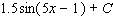
D)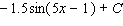
E)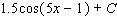
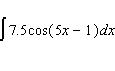
A)
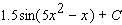
B)
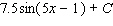
C)
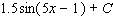
D)
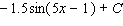
E)
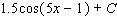

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
58
Evaluate the integral. 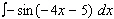
A)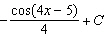
B)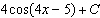
C)
D)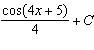
E)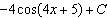
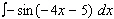
A)
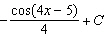
B)
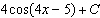
C)

D)
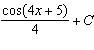
E)
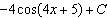

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
59
Evaluate the integral. 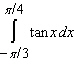
A)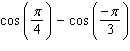
B)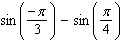
C)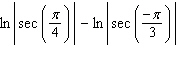
D)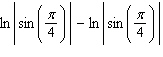
E)none of these
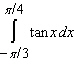
A)
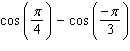
B)
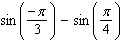
C)
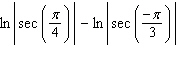
D)
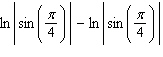
E)none of these

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
60
Evaluate the integral. 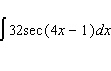
A)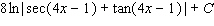
B)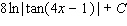
C)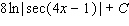
D)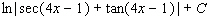
E)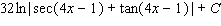
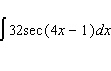
A)
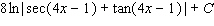
B)
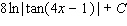
C)
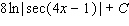
D)
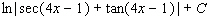
E)
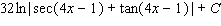

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
61
Match between columns

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
62
Evaluate the integral. 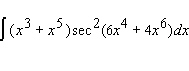 Use the symbol C to write the constant.
Use the symbol C to write the constant.
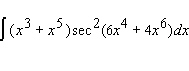 Use the symbol C to write the constant.
Use the symbol C to write the constant.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
63
Recall that the total income received from time t = a to time t = b from a continuous income stream of R (t)dollars per year is 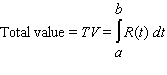 Find the total value of the given income stream and also find its future value (at the end of the given interval)using the given interest rate.
Find the total value of the given income stream and also find its future value (at the end of the given interval)using the given interest rate. 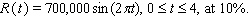
A)TV = $1,400,000, FV = $745,106.09
B)TV = $0, FV = $207,020.55
C)TV = $0, FV = $277,680.69
D)TV = $0, FV = $54,779.56
E)none of these
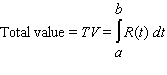 Find the total value of the given income stream and also find its future value (at the end of the given interval)using the given interest rate.
Find the total value of the given income stream and also find its future value (at the end of the given interval)using the given interest rate. 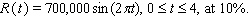
A)TV = $1,400,000, FV = $745,106.09
B)TV = $0, FV = $207,020.55
C)TV = $0, FV = $277,680.69
D)TV = $0, FV = $54,779.56
E)none of these

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
64
Evaluate the integral. 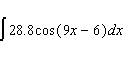 Use the symbol C to write the constant.
Use the symbol C to write the constant.
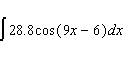 Use the symbol C to write the constant.
Use the symbol C to write the constant.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
65
Evaluate the integral. 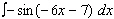
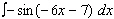

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
66
Decide whether the integral converges. If the integral converges, compute its value. 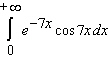
A)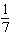
B)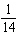
C)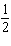
D)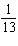
E)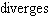
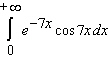
A)
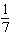
B)
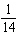
C)
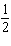
D)
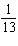
E)
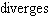

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck