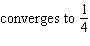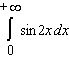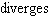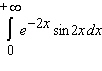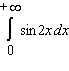Exam 9: Trigonometric Models
Exam 1: Functions and Linear Models100 Questions
Exam 2: Nonlinear Functions and Models88 Questions
Exam 3: Introduction to the Derivative140 Questions
Exam 4: Techniques of Differentiation With Applications106 Questions
Exam 5: Further Applications of the Derivative85 Questions
Exam 6: The Integral71 Questions
Exam 7: Further Integration Techniques and Applications of the Integral117 Questions
Exam 8: Functions of Several Variables133 Questions
Exam 9: Trigonometric Models66 Questions
Select questions type
Decide whether the integral converges. If the integral converges, compute its value. 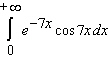
Free
(Multiple Choice)
4.8/5  (30)
(30)
Correct Answer:
B
Recall that the average of a function 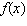 on an interval
on an interval 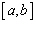 is
is 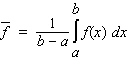 Find the average of the given function.
Find the average of the given function. 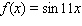 over
over 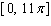 .
.
(Multiple Choice)
4.8/5  (41)
(41)
Use the conversion formula 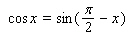 to replace the expression
to replace the expression 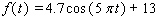 by a sine function.
by a sine function.
(Multiple Choice)
4.9/5  (44)
(44)
Recall that the total income received from time t = a to time t = b from a continuous income stream of R (t)dollars per year is 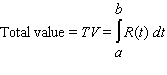 Find the total value of the given income stream and also find its future value (at the end of the given interval)using the given interest rate.
Find the total value of the given income stream and also find its future value (at the end of the given interval)using the given interest rate. 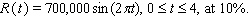
(Multiple Choice)
4.9/5  (41)
(41)
Model the curve with a sine function. 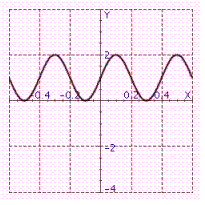 Note that the period of the curve is
Note that the period of the curve is 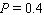 and its range is
and its range is 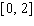 . Write the model function as a function of (x)and
. Write the model function as a function of (x)and 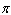 .
.
(Essay)
4.7/5  (33)
(33)
The depth of water 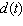 at my favorite surfing spot varies from 9 to 20 feet, depending on the time. Last Sunday high tide occurred at 5:00 A.M. and the next high tide occurred at 6:30 P.M. Use a sine function to model the depth of water as a function of time t in hours since midnight on Sunday morning.
at my favorite surfing spot varies from 9 to 20 feet, depending on the time. Last Sunday high tide occurred at 5:00 A.M. and the next high tide occurred at 6:30 P.M. Use a sine function to model the depth of water as a function of time t in hours since midnight on Sunday morning.
(Multiple Choice)
4.8/5  (27)
(27)
Decide whether each integral converges. If the integral converges, compute its value. Choose the correct letter for each question.
Correct Answer:
Premises:
Responses:
(Matching)
4.8/5  (46)
(46)
Use the conversion formula 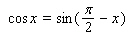 to replace the expression
to replace the expression 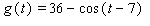 by a sine function.
by a sine function.
(Multiple Choice)
4.9/5  (30)
(30)
Model the curve with a cosine function. 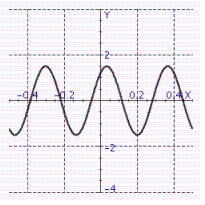 Note that the period of the curve is
Note that the period of the curve is 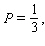 its range is
its range is 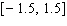 and the graph of the cosine function is shifted to the right 0.7 units.
and the graph of the cosine function is shifted to the right 0.7 units.
(Multiple Choice)
4.7/5  (25)
(25)
Showing 1 - 20 of 66
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)