Deck 2: Equations, Inequalities, and Problem Solving
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/50
Play
Full screen (f)
Deck 2: Equations, Inequalities, and Problem Solving
1
Use the properties of equality to solve the equation.
A)
B)
C)
D)
E)none of these
A)
B)
C)
D)
E)none of these
2
Solve the equation.
A)x = -9
B)x = -7
C)x = -13
D)x = 13
E)x = -5
A)x = -9
B)x = -7
C)x = -13
D)x = 13
E)x = -5
x = -9
3
Solve the equation. 0.11 t - 2.1 = 0.06 t - 0.3
A)t = -36
B)t = 108
C)t = 36
D)t = 72
E)t = 34
A)t = -36
B)t = 108
C)t = 36
D)t = 72
E)t = 34
t = 36
4
Solve the equation. n + 0.5 n = 90
A)n = 90
B)n = 0.5
C)n = -29.5
D)n = 60
E)n = 149.5
A)n = 90
B)n = 0.5
C)n = -29.5
D)n = 60
E)n = 149.5

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
5
Use a property of equality to solve the equation.
A)
B) .
C)
D)
E)
A)
B) .
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
6
When two lines intersect as in the illustration below, four angles are formed. Angles that are side-by-side, such as and , are called adjacent angles. Angles that are nonadjacent, such as and or and , are called vertical angles. From geometry, we know that if two lines intersect, vertical angles have the same measure. If and , find x . Read as "the measure of ". 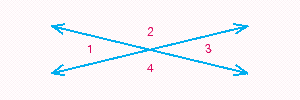
A)x = 11
B)x = 15
C)x = 6
D)x = 8
E)x = 10

A)x = 11
B)x = 15
C)x = 6
D)x = 8
E)x = 10

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
7
Use an equation to solve the problem. Sales tax on a $14 compact disc is $0.84. At what rate is sales tax computed?
A)2%
B)6%
C)8%
D)5%
E)3%
A)2%
B)6%
C)8%
D)5%
E)3%

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the equation. If the equation is an identity or a contradiction, so indicate. 8 x - 2(5 x + 4)= 2( x + 5)
A)
B)
C)
D)identity
E)contradiction
A)
B)
C)
D)identity
E)contradiction

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
9
Use an algebraic approach to solve the problem: Find a number such that one-half of the number is 5 less than two-thirds of the number.
A)15
B)30
C)25
D)35
E)20
A)15
B)30
C)25
D)35
E)20

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
10
The amount A in an account is given by the formula A = p + i where p is the principal and i is the interest. How much interest was earned if an original deposit (the principal)of $4,250 has grown to be $4,520?
A)$280
B)$270
C)$255
D)$275
E)$250
A)$280
B)$270
C)$255
D)$275
E)$250

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
11
Eva invested a certain amount of money at 13% interest and $2,500 more than that amount at 15%. Her total yearly interest was $1,775. How much did she invest at each rate?
A)$2,500 at 13%, $5,000 at 15%
B)$5,000 at 13%, $7,500 at 15%
C)$5,200 at 13%, $7,300 at 15%
D)$5,200 at 13%, $7,700 at 15%
E)$7,500 at 13%, $5,000 at 15%
A)$2,500 at 13%, $5,000 at 15%
B)$5,000 at 13%, $7,500 at 15%
C)$5,200 at 13%, $7,300 at 15%
D)$5,200 at 13%, $7,700 at 15%
E)$7,500 at 13%, $5,000 at 15%

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
12
Solve the equation. 0.43 x + 0.4(8,000 - x )= 3350
A)x = 5,000
B)x = 3,000
C)x = -3,000
D)x = 8,000
E)no solution
A)x = 5,000
B)x = 3,000
C)x = -3,000
D)x = 8,000
E)no solution

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
13
Use the properties of equality to solve the equation.
A)
B)
C)
D)
E)none of these
A)
B)
C)
D)
E)none of these

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
14
Solve the equation.
A)
B)
C)
D)
E)no solution
A)
B)
C)
D)
E)no solution

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
15
Use an algebraic approach to solve the problem: Suppose that the width of a certain rectangle is 2 inch more than one-fourth of its length. The perimeter of the rectangle is 24 inches. Find the length and width of the rectangle.
A)5 inches wide, 7 inches long
B)2 inches wide, 10 inches long
C)3 inches wide, 9 inches long
D)4 inches wide, 8 inches long
E)7 inches wide, 5 inches long
A)5 inches wide, 7 inches long
B)2 inches wide, 10 inches long
C)3 inches wide, 9 inches long
D)4 inches wide, 8 inches long
E)7 inches wide, 5 inches long

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
16
Use an algebraic approach to solve the problem: A board 20 feet long is cut into two pieces such that the length of one piece is two-thirds of the length of the other piece. Find the length of the shorter piece of board.
A)20 feet
B)4 feet
C)12 feet
D)-4 feet
E)8 feet
A)20 feet
B)4 feet
C)12 feet
D)-4 feet
E)8 feet

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
17
Use a property of equality to solve the equation.
A)-147
B)- 152
C)- 153
D)- 137
E)- 144
A)-147
B)- 152
C)- 153
D)- 137
E)- 144

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
18
Use an equation to solve the problem. The average price of homes in one neighborhood decreased 8% since last year, a drop of $5,400. What was the average price of a home last year?
A)$64,500
B)$69,500
C)$68,500
D)$67,500
E)$71,500
A)$64,500
B)$69,500
C)$68,500
D)$67,500
E)$71,500

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the equation. 5( t - 2)+ 2( t - 1)= -2( t - 1)+ 10( t + 2)
A)t = -44
B)t = -36
C)t = -34
D)t = -29
E)t = -27
A)t = -44
B)t = -36
C)t = -34
D)t = -29
E)t = -27

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
20
Solve the equation.
A)x = 11
B)x = -10
C)x = 3
D)x = 10
E)x = 20
A)x = 11
B)x = -10
C)x = 3
D)x = 10
E)x = 20

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
21
The perimeter of a rectangle with length I and width W is given by the formula . Solve this formula for W . If the perimeter of a certain rectangle is 46.54 meters and its length is 16.25 meters, find its width.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
22
Solve the inequality.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
23
The masses of two objects are and . The force of gravitation F between the masses is given by where is a constant and is the distance between them. Solve for .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
24
Solve the formula for B . Volume of a pyramid:
A)
B)
C)
D)
E)none of these
A)
B)
C)
D)
E)none of these

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
25
Solve the inequality.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
26
Solve the formula for the variable .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
27
For the following problem, solve the inequality and express the solution set using interval notation.
A)
B)
C)
D)
E)none of these
A)
B)
C)
D)
E)none of these

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the inequality.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
29
Solve the inequality. Write the answer in interval notation.
A)
B)
C)
D)no solution
A)
B)
C)
D)no solution

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the inequality. -2 x ≥ 6
A)x ≥ -3
B)x ≠ -3
C)x ≤ 3
D)x
E)x ≤ -3
A)x ≥ -3
B)x ≠ -3
C)x ≤ 3
D)x
E)x ≤ -3

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the formula for the variable .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the formula for the variable r . Then substitute numbers i = 90 , p = 200, and t = 5 to find the variable's value.
A)r = 105
B)r = - 115
C)r = 0.09
D)r = 295
E)r = 0.45
A)r = 105
B)r = - 115
C)r = 0.09
D)r = 295
E)r = 0.45

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the formula for the variable .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the inequality and express the solution set using interval notation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
35
Solve the compound inequality. Graph the solution set (if one exists)and write it using interval notation. and
A)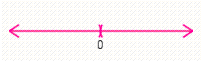
B)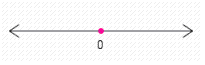
C)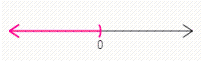
D)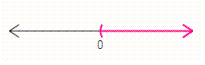
E)
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the inequality. Graph the result.
A)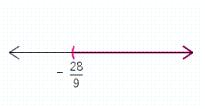
B)
C)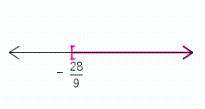
D)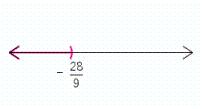
E)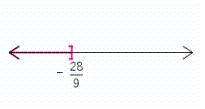
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
37
Solve the inequality and express the solution set using interval notation.
A)(- ?, -26)
B)(-26, ?)
C)(- ?, -11)
D)(-11, ?)
E)(26, ?)
A)(- ?, -26)
B)(-26, ?)
C)(- ?, -11)
D)(-11, ?)
E)(26, ?)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
38
Graph the solution set.
A)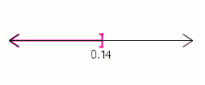
B)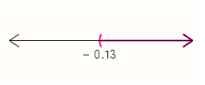
C)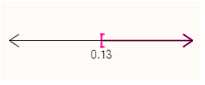
D)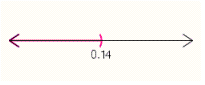
E)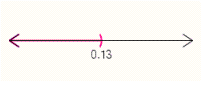
A)
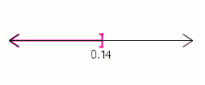
B)
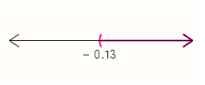
C)

D)

E)


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
39
Solve A = P + Prt for A , given that P = $1100, , and t = 11 years.
A)A = $2,057.50
B)A = $2,007.50
C)A = $907.50
D)A = $2,307.50
E)A = $1,907.50
A)A = $2,057.50
B)A = $2,007.50
C)A = $907.50
D)A = $2,307.50
E)A = $1,907.50

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
40
The power lost when an electric current passes through a resistance is given by the formula . Solve for . If is 2,900 watts and is 16 amperes, calculate to the nearest hundredth of an ohm.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the inequality.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the equation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
43
Solve the problem by setting up and solving an appropriate inequality. Sue bowled 150 and 140 in her first two games. What must she bowl in the third game to have an average of at least 170 for the three games?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
44
To hold the temperature of a room between and what Fahrenheit temperatures must be maintained?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
45
How long can a person rent the truck described in the ad if the cost is to be less than $120? Round your answer to the nearest hour. ACTION Truck Rental Big Truck Only \$26.95 for one hour. for each extra hour.
A)Approximately 10 hr
B)Approximately 8 hr
C)Approximately 12 hr
D)Approximately 15 hr
E)Approximately 7 hr
A)Approximately 10 hr
B)Approximately 8 hr
C)Approximately 12 hr
D)Approximately 15 hr
E)Approximately 7 hr

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the equation, if possible.
A)8, -16
B)8
C)8, 16
D)-8 , -16
E)no solution
A)8, -16
B)8
C)8, 16
D)-8 , -16
E)no solution

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the equation, if possible.
A)
B)
C)
D)
E)no solution
A)
B)
C)
D)
E)no solution

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the equation.
A)x = -5, x = 9
B)x = 9
C)x = 5, x = 9
D)x = 5
E)x = -5, x = -9
A)x = -5, x = 9
B)x = 9
C)x = 5, x = 9
D)x = 5
E)x = -5, x = -9

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the equation. Give the solution in interval notation.
A)
B)
C)
D)
E)no solution
A)
B)
C)
D)
E)no solution

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the inequality. Use interval notation to describe the solution.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck


