Deck 13: Factorial Anova: Fixed-Effects Mode

Question 1

Complete the following ANOVA summary table for a two-factor fixed-effects ANOVA, where there are three levels of factor A (teaching method) and two levels of factor B (time of class).
Each cell includes six students and $\alpha$ = .05.

$\begin{array}{ccccccc}\hline \text { Source } & S S & d f & M S & F & \text { Critical Value } & \text { Decision } \\\hline \text { A } & & & 6.5 & & & \\\text { B } & & & & & \\\mathrm{AB} & & & 5.2 & & \\\text { Within } & 39 & & & & \\\text { Total } & 65 & & & & \\\hline\end{array}$

Answer 1

There are 3 levels of factor A, so J = 3. There are 2 levels of factor B, so K = 2. Each cell has 6 students, so n = 6. N = 3*2*6 = 36.

df_A = J - 1 = 3 - 1 = 2, df_B = K- 1 = 2 - 1 = 1, df_AB = (J - 1)(K - 1) = 2*1 = 2, df_with = N - JK = 36 - 3*2 = 30, df_total = N- 1 = 36 - 1 = 35.

SS_A = df_A*MS_A = 2*6.5 = 13, SS_AB = df_AB*MS_AB = 2*5.2 = 10.4,
SS_B = SS_total -SS_A - SS_AB -SS_with = 65 - 13 - 10.4- 39 = 2.6.

MS_B = SS_B/df_B = 2.6/1 = 2.6; MS_with = SS_with/df_with = 39/30 = 1.3.

F_A = MS_A/MS_with = 6.5/1.3 = 5; critical value = _.05F_2,30 = 3.32 < F_A, reject H₀.
F_B=MS_B/MS_with = 2.6/1.3 = 2; critical value = _.05F_1,30 = 4.17 > F_B, fail to reject H₀.

F_AB =MS_AB/MS_with =5.2/1.3 = 4; critical value = _.05F_2,30 = 3.32 < F_AB, reject H₀.

$\begin{array}{ccccccc}\hline \text { Source } & S S & \boldsymbol{d f} & M S & F & \text { Critical Value } & \text { Decision } \\\hline \mathrm{A} & 13.0 & 2 & 6.5 & 5 & .05 F_{2,00}=3.32 & \text { Reject } H_{0} \\\mathrm{~B} & 2.6 & 1 & 2.6 & 2 & .05 F_{1,30}=4.17 & \text { Fail toreject } H_{0} \\\mathrm{AB} & 10.4 & 2 & 5.2 & 4 & .05 F_{2,30}=3.32 & \text { Reject } H_{0} \\\text { Within } & 39.0 & 30 & 1.3 & & & \\\text { Total } & 65.0 & 35 & & & & \\\hline\end{array}$

Question 2

Complete the following ANOVA summary table for a two-factor fixed-effects ANOVA, where there are four levels of factor A (grade level) and three levels of factor B (textbook). Each cell includes 11 students and $\alpha$ = .05.

$\begin{array}{ccccccc}\hline \text { Source } & S S & d f & M S & F & \text { Critical Value } & \text { Decision } \\\hline \mathrm{A} & & & 5 & & \\\mathrm{~B} & 42 & & & & \\\mathrm{AB} & & & 25 & & \\\text { Within } & 240 & & & & \\\text { Total } & & & & & & \\\text { Win }\end{array}$

Answer 2

A has 4 levels, so J = 4. B has 3 levels, so K = 3. Each cell has 11 students, so n = 11. N = 4*3*11 = 132.

df_A = J- 1 = 4 - 1 = 3, df_B = K - 1 = 3 - 1 = 2, df_AB = (J - 1)(K - 1) = 3*2 = 6, df_with = N - JK = 132 - 4*3 = 120, df_total = N - 1 = 132 - 1 = 131.

SS_A = df_A*MS_A = 3*5 = 15, SS_AB = df_AB*MS_AB = 6*25 = 150,
SS_total = SS_A + SS_B + SS_AB + SS_with = 15 + 42 + 150 + 240 = 447.

MS_B = SS_B/df_B = 42/2 = 21; MS_with = SS_with/df_with = 240/120 = 2.

F_A =MS_A/MS_with = 5/2 = 2.5; critical value = _.05F_3,120 = 2.68 > F_A, fail to reject H₀.
F_B =MS_B/MS_with = 21/2 = 10.5; critical value = _.05F_2,120 = 3.07 < F_B, reject H₀.

F_AB =MS_AB/MS_with = 25/2 = 12.5; critical value = _.05F_6,120 = 2.18 < F_AB, reject H₀.

$\begin{array}{ccccccc}\hline \text { Source } & S S & d f & M S & F & \text { Critical Value } & \text { Decision } \\\hline \text { A } & 15 & 3 & 5 & 2.5 & 05 F_{3,100}=2.68 & \text { Fail to reject } H_{0} \\\mathrm{~B} & 42 & 2 & 21 & 10.5 & 05 F_{2120}=3.07 & \text { Reject } H_{0} \\\mathrm{AB} & 150 & 6 & 25 & 12.5 & 05 F_{6,100}=2.18 & \text { Reject } H_{0} \\\text { Within } & 240 & 120 & 2 & & & \\\text { Total } & 447 & 131 & & & & \\\hline\end{array}$

Question 3

Complete the following ANOVA summary table for a two-factor fixed-effects ANOVA, where there are two levels of factor A (type of counseling) and four levels of factor B (frequency of counseling). Each cell includes six people and $\alpha$ = .01.

$\begin{array}{ccccccc}\hline \text { Source } & S S & d f & M S & F & \text { Critical Value } & \text { Decision } \\\hline \mathrm{A} & 60 & & & 6 & \\\mathrm{~B} & & & & & \\\mathrm{AB} & 60 & & & & \\\text { Within } & & & & & \\\text { Total } & 640 & & & & \\\hline\end{array}$

Answer 3

A has 2 levels, so J = 2. B has 4 levels, so K = 4.

Each cell has 6 people, so n = 6. N = 2*4*6 = 48.

df_A = J - 1 = 2 - 1 = 1, df_B = K - 1 = 4 - 1 = 3, df_AB = (J - 1)(K - 1) = 1*3 = 3, df_with = N - JK = 48 - 2*4 = 40, df_total = N - 1 = 48 - 1 = 47.

MS_A = SS_A/df_A = 60/1 = 60, MS_AB = SS_AB/df_AB = 60/3 = 20,
MS_with = MS_A/F_A = 60/6 = 10; SS_with = MS_with*df_with = 10*40 = 400,
SS_B = SS_total - SS_A - SS_AB - SS_with = 640 - 60 - 60 - 400 = 120;
MS_B = MS_B/F_B = 120/3 = 40
F_A = MS_A/MS_with = 60/10 = 6; critical value = _.01F_1,40 = 7.31 > F_A, fail to reject H₀.

F_B = MS_B/MS_with = 40/10 = 4; critical value = _.01F_3,40 = 4.31 > F_B, fail to reject H₀.
F_AB = MS_AB/MS_with = 20/10 = 2; critical value = _.01F_3,40 = 4.31 > F_AB, fail to reject H₀.

$\begin{array}{crrrrcc}\text { Source } & S S & d f & M S & F & \text { Critical Value } & \text { Decision } \\\hline \mathrm{A} & 60 & 1 & 60 & 6 & .01 F_{1,40}=7.31 & \text { Fail to reject } H_{0} \\\mathrm{~B} & 120 & 3 & 40 & 4 & .01 F_{3,40}=4.31 & \text { Fail to reject } H_{0} \\\mathrm{AB} & 60 & 3 & 20 & 2 & .01 F_{3,40}=4.31 & \text { Fail to reject } H_{0} \\\text { Within } & 400 & 40 & 10 & & & \\\hline\end{array}$

Question 4

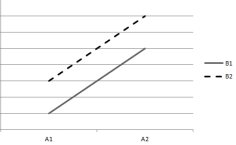
Questions are based on the following plots of cell means. Assume that the within-cell variation is very small.
(1)
(2)
(3)
( 4)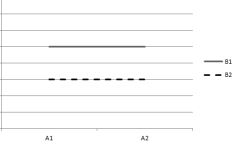

-Which plot indicates that both main effects are significant but the interaction effect is nonsignificant?

A) plot (1)
B) plot (2)
C) plot (3)
D) plot (4)

Question 5

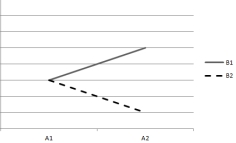
Questions are based on the following plots of cell means. Assume that the within-cell variation is very small.
(1)
(2)
(3)
( 4)

-Which plot indicates that neither of the main effects are significant but the interaction effect is significant?

A) plot (1)
B) plot (2)
C) plot (3)
D) plot (4)

Question 6

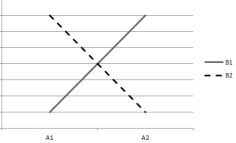
Questions are based on the following plots of cell means. Assume that the within-cell variation is very small.
(1)
(2)
(3)
( 4)

-Which plot(s) indicate(s) significant interaction effects?

A) plots (1) and (2)
B) plots (2) and (3)
C) plots (1), (2), and (3)
D) plots (1) and (4)

Question 7

The results of a two-factor ANOVA (J = 3, K = 2) show that both main effects are significant, but the interaction is not significant. We need to

A) conduct MCPs to examine the two main effects and the interaction effect.
B) conduct MCPs to examine the interaction effect only.
C) conduct MCPs to examine the two main effects.
D) conduct MCPs to examine one main effect only.

Question 8

Questions are based on the following ANOVA summary table (fixed effects):

$\begin{array}{crcc}\hline \text { Source } & \text { df } & \boldsymbol{M S} & F \\\hline \mathrm{A} & 2 & 15 & 3.0 \\\mathrm{~B} & 3 & 10 & 2.0 \\\mathrm{AB} & 6 & 3 & 0.6 \\\text { Within } & 120 & 5 & \\\hline\end{array}$

-For which source of variation is the null hypothesis rejected at the .10 level of significance?

A) A
B) B
C) AB
D) All of the above

Question 9

Questions are based on the following ANOVA summary table (fixed effects):

$\begin{array}{crcc}\hline \text { Source } & \text { df } & \boldsymbol{M S} & F \\\hline \mathrm{A} & 2 & 15 & 3.0 \\\mathrm{~B} & 3 & 10 & 2.0 \\\mathrm{AB} & 6 & 3 & 0.6 \\\text { Within } & 120 & 5 & \\\hline\end{array}$

-How many cells are there in the design?

A) 6
B) 8
C) 9
D) None of the above

Question 10

Questions are based on the following ANOVA summary table (fixed effects):

$\begin{array}{crcc}\hline \text { Source } & \text { df } & \boldsymbol{M S} & F \\\hline \mathrm{A} & 2 & 15 & 3.0 \\\mathrm{~B} & 3 & 10 & 2.0 \\\mathrm{AB} & 6 & 3 & 0.6 \\\text { Within } & 120 & 5 & \\\hline\end{array}$

-The total sample size for the design is which one of the following?

A) 131
B) 132
C) 134
D) None of the above

Question 11

Questions are based on the following ANOVA summary table (fixed effects):

$\begin{array}{cccc}\hline \text { Source } & d f & M S & F \\\hline \mathrm{A} & 5 & 18.0 & 6.0 \\\mathrm{~B} & 1 & 13.5 & 4.5 \\\mathrm{AB} & 5 & 15.0 & 5.0 \\\text { Within } & 60 & 3.0 & \\\hline\end{array}$

-For which source of variation is the null hypothesis rejected at the .05 level of significance?

A) A
B) B
C) AB
D) All of the above

Question 12

Questions are based on the following ANOVA summary table (fixed effects):

$\begin{array}{cccc}\hline \text { Source } & d f & M S & F \\\hline \mathrm{A} & 5 & 18.0 & 6.0 \\\mathrm{~B} & 1 & 13.5 & 4.5 \\\mathrm{AB} & 5 & 15.0 & 5.0 \\\text { Within } & 60 & 3.0 & \\\hline\end{array}$

-How many cells are there in the design?

A) 6
B) 10
C) 12
D) None of the above

Question 13

Questions are based on the following ANOVA summary table (fixed effects):

$\begin{array}{cccc}\hline \text { Source } & d f & M S & F \\\hline \mathrm{A} & 5 & 18.0 & 6.0 \\\mathrm{~B} & 1 & 13.5 & 4.5 \\\mathrm{AB} & 5 & 15.0 & 5.0 \\\text { Within } & 60 & 3.0 & \\\hline\end{array}$

-The total sample size for the design is which one of the following?

A) 72
B) 74
C) 77
D) None of the above

Question 14

Which of the following would be appropriate for a factorial ANOVA?

A) One categorical dependent variable and one categorical independent variable
B) One categorical dependent variable and one continuous independent variable
C) One continuous dependent variable and one categorical independent variable
D) One continuous dependent variable and two categorical independent variables

Question 15

A researcher is interested in examining the extent to which there is a mean difference in lower-class undergraduate students' attitude toward instruction (interval) based on class modality (face-to-face, hybrid, online) and class standing (freshman or sophomore). Would conducting a factorial ANOVA be appropriate for this study?

Question 16

In a two-factor fixed-effects ANOVA with factors A and B, each of which have four categories, which one of the following occurs?

A) Alternating categories of the factors are not included.
B) Categories 1 and 2 of factor A are crossed with categories 3 and 4 of factor B only.
C) Every combination of factors A and B is included in the design of the study.
D) The first one-half of units in each category in factor A are crossed with the last one-half of unit in each category in factor B; other units and categories are excluded.