Deck 10: Introducing Inference: Estimation From Samples
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/20
Play
Full screen (f)
Deck 10: Introducing Inference: Estimation From Samples
1
The purpose of inferential statistics is to make inferences about characteristics of the population from which the data were drawn.
True
2
When both variables are categorical, the t-test should be used for hypothesis testing.
False
3
When both variables are continuous, the χ2 test should be used for hypothesis testing.
False
4
When both variables are continuous, simple regression can be used.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
5
Multivariate statistics involve statistics for three or more variables.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
6
It is practical to survey the entire population of a city.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
7
The population is the entire set of subjects of interest in any study, and a sample is a portion or subset of the population.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
8
Statistical inference is about drawing conclusions about a population from sample data.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
9
The best way to draw a sample is randomly-each subject should have an equal chance of being selected as part of your sample.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
10
We use population parameters to estimate unknown sample statistics.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
11
The estimation error is the difference between a sample statistic and a population parameter.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
12
A confidence interval is defined the range within which the unknown but true population parameter is estimated to lie.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
13
A 95% confidence interval is sometimes expressed as stating that when drawing many samples, 5% of the times the mean will lie within a confidence interval.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
14
The Central Limit Theorem is fundamental statistical insight that allows us to make inferences from a single sample to the population.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
15
A probability distribution is a statistical function which describes all possible values and likelihoods that a variable can take.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
16
A normal distribution (Appendix
A) A) is an example of a probability distribution.
A) A) is an example of a probability distribution.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
17
The standard deviation of a probability distribution is also called a standard error.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
18
The formula for calculating a confidence interval for samples larger than 30 is .
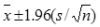
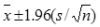

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
19
When the sample size is smaller than 30, the normal distribution is replaced by the t distribution for calculating confidence interval.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
20
Confidence intervals are also calculated for proportions (e.g., polling data)

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck


